Одномерные плоские волны в стержнях постоянного сечения. Метод характеристик. Нестационарные задачи.

Продолжим исследование волн в стержнях постоянного сечения 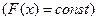. На предыдущей лекции было получены две возможных эквивалентных формы уравнений движения стержня. Если в качестве неизвестной функции выбрать перемещение, то для него справедливо волновое уравнение

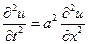. (2.1)

Если в качестве искомых функций выбрать скорость 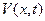и деформацию 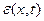сечения 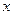, для них справедлива следующая система двух уравнений

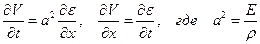. (2.2)

На первой лекции было найдено общее решение уравнения (2.1), которое представляет собой сумму двух бегущих в разные стороны волн.

Рассмотрим теперь систему двух уравнений первого порядка (2.2). Методы решения системы уравнений первого порядка в частных производных очень сильно зависят от «типа» рассматриваемой системы. Сам «тип» системы уравнений определяется соотношением между количеством действительных характеристик и количеством уравнений данной системы. Если количество характеристик совпадает с количеством уравнений, система будет иметь гиперболический тип. Если количество действительных характеристик меньше количества уравнений, но хотя бы одна действительная характеристика есть, система будет иметь параболический тип. Если действительных характеристик нет совсем, то система называется эллиптической. Пока не определено понятие характеристик, тип уравнений определен чисто формально. Поэтому попробуем разобраться с этим важным понятием – понятием характеристики на примере более конкретных систем уравнений.

Помимо типа системы уравнений важную роль для их решения играет то, как в ней участвуют производные искомых функций, а также вид функциональной зависимости коэффициентов при производных и свободных членов данной системы уравнений. Если производные искомых функций входят в систему линейно, такая система называется квазилинейной.

Рассмотрим в плоскости независимых переменных 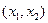квазилинейную систему двух уравнений с двумя неизвестными 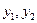, линейную относительно производных этих функций:

,

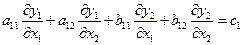(2.3)

,

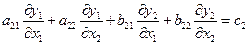где коэффициенты 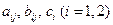могут быть функциями независимых переменных 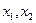и искомых функций .

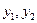Такие квазилинейные системы в свою очередь можно определить по следующим признакам:

1.Если все коэффициенты являются функциями только независимых переменных, система уравнений называется линейной.

2.Если коэффициенты 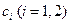равны нулю, система называется однородной.

3.Если система уравнений – квазилинейная и однородная, она называется приводимой.

4.Если перечисленных признаков нет, это квазилинейная система общего вида.

Отметим, что система уравнений (2.1) является согласно данным определениям одновременно и линейной и однородной, т.е. линейной и приводимой.

Поставим для системы (2.3) следующую задачу:

На некоторой кривой 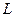в плоскости независимых переменных 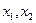заданы значения искомых функций 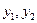. Требуется найти решение в сколь угодно малой окрестности данной кривой 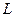. Такая задача называется задачей Коши.

Вдоль кривой независимые переменные связаны дифференциальным равенством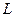

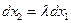, (2.4)

а дифференциалы искомых функций 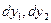вдоль данной кривой заданы, поскольку на кривой заданы сами функции. Это означает, что на самой кривой нам известны правые части выражений

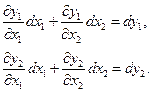(2.5)

Отметим, что разложение произвольной функции в ряд в окрестности некоторой точки позволяет определить функцию в том случае, когда известны значения производных в данной точке разложения

.

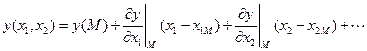Это означает, что если бы нам удалось найти первые производные искомых функций в любой точке кривой 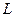, то мы нашли бы значения этих функций в малой окрестности данной точки, т.е. решили бы задачу Коши.

Определение 1.Кривая 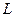называется характеристической (или характеристикой) системы уравнений (2.3), если задача Коши на ней не имеет бесконечно много решений.

Для того, чтобы найти эти особые линии – характеристики, рассмотрим систему уравнений четвертого порядка для производных искомых функций, которая составлена из уравнений (2.3), (2.5)

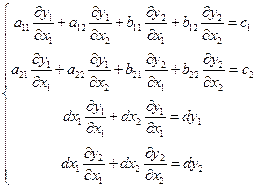. (2.6)

Относительно производных искомых функций мы получили для кривой 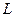линейную систему четвертого порядка. Система имеет бесконечно много решений тогда, когда определитель системы и ее дополнительные определители равны нулю. Приравняем к нулю определитель

.

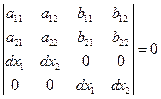В результате получим уравнение, связывающее полные дифференциалы независимых переменных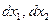

.

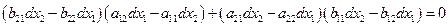Для угла наклона 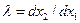данной кривой мы получим квадратное уравнение

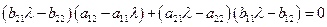. (2.7)

Уравнение (2.7) в зависимости от коэффициентов может иметь два действительных корня, один действительный корень или не иметь действительных корней совсем. Таким образом, данное уравнение определяет количество характеристик и дает возможность, если они есть, определить сами характеристические кривые, как решения обыкновенного дифференциального уравнения

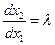, (2.8)

где 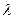один из действительных корней (2.7). Если характеристика существует, то потребовав равенство нулю дополнительных определителей, мы можем получить дифференциальное уравнение для самих искомых функций, справедливое на этой характеристике. Обычно оно называется условием совместности.

Рассмотрим в качестве примера систему уравнений (2.2). Поставим следующее соответствие искомых функций 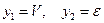и независимых переменных 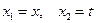. Тогда расширенная матрица системы (2.6) будет иметь конкретный вид

.

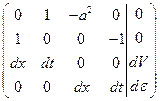Приравнивая к нулю ее определитель, получим уравнения характеристик

,

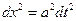или

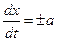. (2.9)

Приравнивая дополнительные определители и используя связь (2.9), получим условия совместности на характеристиках

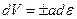. (2.10)

Полученный результат позволяет сказать, что система уравнений (2.2) имеет гиперболический тип.

Можно дать и еще несколько определений характеристики. Все они эквивалентны и если какое-то определение принимается за основу, то все остальные можно назвать свойствами характеристики.

Мы рассмотрим еще два возможных определения понятия характеристики.

Определение 2.Кривая 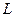называется характеристической (или характеристикой) системы уравнений (2.3), если вдоль этой кривой система может быть записана в полных дифференциалах.

Покажем эквивалентность данного определения на примере системы (2.2). Для этого поставим задачу отыскания такой линии 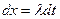в плоскости независимых переменных 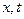, вдоль которых система примет вид уравнения в полных дифференциалах. Для этой цели умножим первое уравнение на 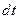, второе – на дифференциал 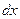и сложим. В результате, с учетом искомой связи 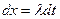, получим уравнение

.

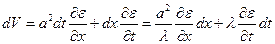Уравнение может быть записано в полных дифференциалах, когда коэффициенты в правой части при производных функции 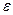будут равны. Отсюда мы получим уравнения самих характеристик

,

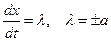и уравнения, которые должны выполняться вдоль этих характеристик

.

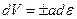Как видим данные соотношения полностью совпадают с полученными ранее уравнениями (2.9), (2.10).

Определение 3.Кривая 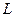называется характеристической (или характеристикой) системы уравнений (2.3), если она является возможным местом слабых разрывов решения (т.е. по ней распространяются малые возмущения).

Для прояснения введенных понятий определим. Что мы будем понимать под словами малые возмущения. Пусть в плоскости независимых переменных существует кривая, на которой сами искомые функции непрерывны, а хотя бы одна из производных терпит разрыв (такой разрыв называется слабым). Разрыв производной любого порядка будем считать малым возмущением или слабым разрывом. Покажем, что линиями слабого разрыва могут быть только характеристики системы. Применим операцию скачка к уравнениям системы (2.3) и к полным дифференциалам искомых функций (2.5), тогда для скачков производных получим однородную систему уравнений

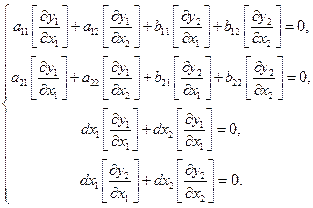
Поскольку на искомой линии хотя бы одна из производных терпит разрыв, система должна иметь нетривиальное решение. Но это возможно только в том случае, когда ее определитель равен нулю. Поскольку определители (2.6) и полученной системы совпадают, линии слабого разрыва будут одновременно характеристиками. Физическим результатом будет то, что волны слабого разрыва распространяются по характеристикам. Покажем, как используются характеристики и их свойства при решении конкретных задач с начальными и граничными условиями для гиперболических систем уравнений.