Метод характеристик.

Рассмотрим применение характеристик для получения решения в нестационарных динамических задачах. Для этого рассмотрим следующую задачу:

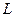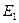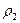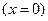Первый стержень длиной , изготовленный из материала с плотностью и модулем Юнга жестко состыкован с другим бесконечным стержнем, изготовленным из материала с плотностью и модулем Юнга . В начальный момент времени оба стержня находятся в невозмущенном состоянии. Затем, начиная с отсчетного времени , на левом торце первого стержня начинает действовать сжимающая нагрузка 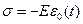, где заданная функция (Рис.1). Требуется определить деформации и скорости сечений стержней в моменты времени .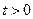

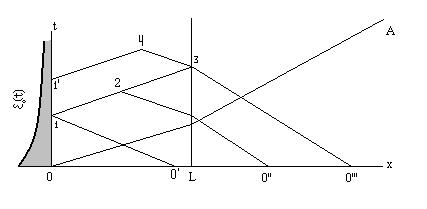
Рис.1

В соответствии с постановкой задачи имеем следующие начальные и граничные условия:

;

;

;

.

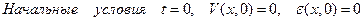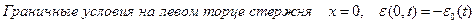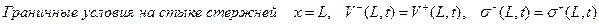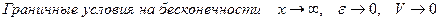Основу метода характеристик составляет последовательное определение решения во всех характерных точках, влияющих на решение в рассматриваемой точке. Обозначим скорости волн в стержнях.

Допустим, что надо определить решение в точках лежащих ниже линии 0А (рис.1). Проинтегрируем условия (2.10) вдоль характеристик, приходящих в соответствующую точку. Полученное конечное соотношение на характеристике будет содержать произвольную константу. Для рассматриваемых точек приходящие характеристики пересекаются с линией , где и скорость и деформация равны нулю, поэтому постоянные интегрирования для обеих характеристик будут равны нулю. Поскольку в данной точке, принадлежащей характеристикам обеих семейств, должны выполняться оба соотношения, мы получим для искомых величин (скорости и деформации) два уравнения с двумя неизвестными. Решая, находим:

.

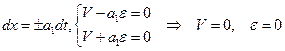Для точки (1) (рис.1) система уравнений получается, если к условию на характеристике отрицательного наклона, приходящей в данную точку (постоянная интегрирования на ней равна в силу начальных условий нулю), добавить граничное условие:

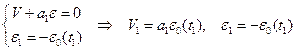. (2.11)

Вдоль характеристики (1;2) получим условие, для которого постоянная интегрирования определяется уже найденным решением в точке (1):

.

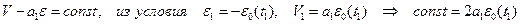Для определения решения в точке (3) необходимо привлечение граничных условий на контактной поверхности и условий на приходящих в данную точку характеристиках 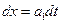и :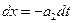

На характеристике (1;3) имеем уравнение ;

На характеристике (0’’;3) имеем уравнение ;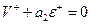

Условия на контактной поверхности .

Решая систему четырех уравнений с четырьмя неизвестными, находим решение в точке (3)

, (2.12)

где 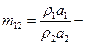отношение акустических импедансов материалов стержней.

Для получения решения в точке (4) нам потребуется знание решения в точках (1’) и (3). Вдоль характеристики ( 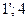) имеем условие 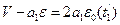, а вдоль характеристики (3;4) соответственно условие 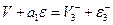. Привлекая найденное в точке (3) (рис.1) решение (2.12), получим

.

Отметим роль акустического импеданса. Если 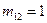отраженной волны нет, поскольку решение в точке (4) полностью описывается параметрами идущей слева волны.

Данный процесс может быть продолжен для точек плоскости независимых переменных, которым соответствуют большие времена, т.е. решение может быть последовательно продолжено и получено для любой произвольной точки с координатами . В современной практике приведенное решение строится с помощью ЭВМ, поскольку алгоритм его нахождения достаточно прост. Разбив время выбранным дискретным шагом, мы для каждого очередного шага по времени решаем одинаковую задачу. Меняются только условия на предыдущем шаге. Возможность получения фактически точного решения, очень малые требования к памяти и простой алгоритм реализации делают метод характеристик одним из самых употребительных в динамических задачах.