Исследование формы эллипса

Так как в каноническое уравнение эллипса координаты х и у входят в четной степени (именно во второй), то если на эллипсе

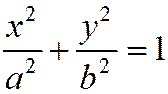(1)

лежит точка М(х,у), т. е. координаты это точки удовлетворяют уравнению (1), то на том же эллипсе лежат точк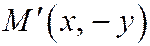и и 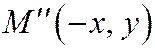, симметричные с точкой М относительно осей Ох и Оу,и точка 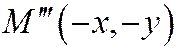, симметричная с точкой М относительно начала координат. Поэтому оси координат Ох и Оу для

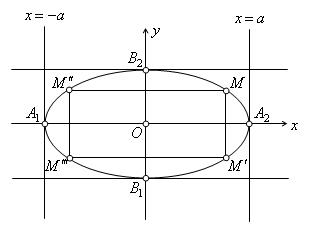эллипса, заданного каноническим уравнением (1) являются осями симметрии, а начало координат – центром симметрии. Из уравнения эллипса 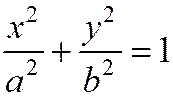следует, что для координат любой его точки имеют место соотношения

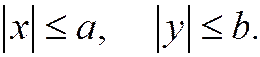
Геометрически это значит, что эллипс расположен внутри прямоугольника, сторонами которого являются прямые

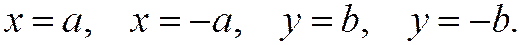
Точки пересечения эллипса с его осями симметрии называются вершинами эллипса. Таким образом, эллипс (1) имеет 4 вершины: , , , .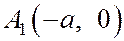

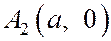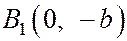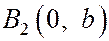Полуосью эллипса называется отрезок (а также длина этого отрезка), одним концом которого является центр симметрии эллипса, а другим – одна из его вершин; а называется большей полуосью эллипса, а b – меньшей полуосью.

Отрезок 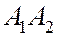- большая ось эллипса.

Отрезок 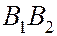- меньшая ось эллипса.

Замкнутая линия является выпуклой, если любая прямая пересекает ее не более чем в двух точках. Эллипс есть выпуклая замкнутая линия, так как решая уравнение (1) эллипса совместно с уравнением прямо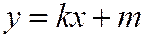й или 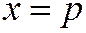, получим уравнение второй степени относительно х или у, значит, любая прямая пересекает эллипс не более чем в двух точках.

Итак, эллипс – замкнутая выпуклая линия, имеющая центр симметрии и две (взаимно перпендикулярные) оси симметрии.

Условимся уравнение 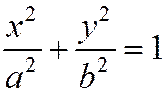называть каноническим уравнением эллипса и в том случае, когда а = b и когда a < b.

В случае а = b уравнение примет вид

,

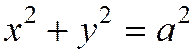т.е. является уравнением окружности радиуса а с центром в начале координат. Таким образом, мы рассматриваем окружность как частный случай эллипса. Этот частный случай соответствует совпадению фокусов 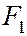и 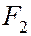с центром окружности.

В случае а < b большей полуосью будет b, а меньшей - а. Фокусы будут расположены на оси Оу на расстоянии 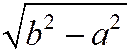от центра эллипса.

Отношение половины расстояния между фокусами эллипса (фокальное расстояние) к большей полуоси эллипса называется эксцентриситетом эллипса и обозначается буквой е:

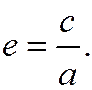
Так как 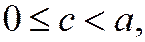то 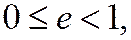т. е. эксцентриситет эллипса есть неотрицательное число, меньшее единицы.

Отметим, что 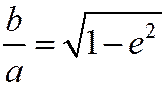(поскольку ).

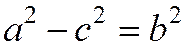Следовательно, эксцентриситет определяется отношением полуосей эллипса, и, обратно, отношение полуосей эллипса определяет его эксцентриситет.

Если эксцентриситет равен нулю е = 0, то а = b и эллипс является окружностью. Чем ближе эксцентриситет е к 1, тем меньше 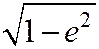и, значит, тем меньше отношение меньшей полуоси к большей. Таким образом, эксцентриситет характеризует степень «вытянутости» эллипса.

Вспоминая формулы:

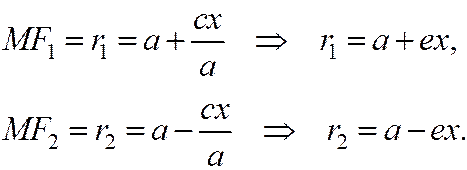
Директрисы эллипса

Две прямые, перпендикулярные оси эллипса, на которой расположены его фокусы, и отстоящие от центра эллипса на расстоянии 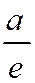,где а - большая полуось эллипса, ае - его эксцентриситет, называются директрисами эллипса.

Окружность, для которой е = 0 не имеет директрис 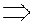т.е. понятие директрис дается только для эллипса.

Если эллипс задан каноническим уравнением, причем 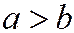(т.е. фокусы расположены на оси Ох) то уравнения директрис имеют вид:

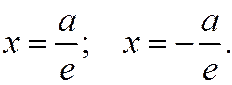
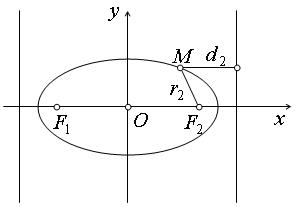
Так как 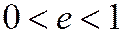; то 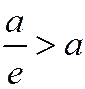, и, значит, директрисы эллипса отстоят от его центра дальше, чем вершины (см. рис.). Фокус и директриса эллипса, расположенные по одну сторону от меньшей оси эллипса, называются соответствующими друг другу.

Таким образом, фокусы 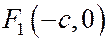соответствует директриса 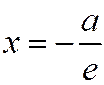, а фокусу 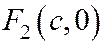- директриса .

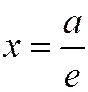Теорема. Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение расстояния от этой точки до фокуса эллипса к расстоянию от той же точки до директрисы, соответствующей рассматриваемому фокусу, было равно эксцентриситету эллипса.

Доказательство: Необходимость. Рассмотрим, например, фокус 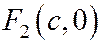и соответствующую ему директрису 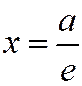. Расстояние 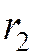от точки М(х, у) до

фокуса 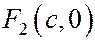вычисляется по формуле .

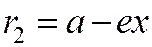Расстояние 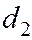от той же точки М(х, у) эллипса до прямой 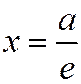вычисляется по формуле .

Итак: .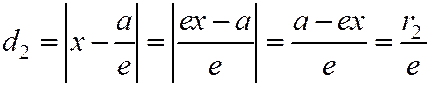

Отсюда 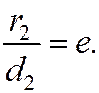Теорема доказана.

Аналогично доказывается, что 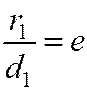, где 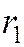, есть расстояние от точки М до фокус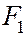а , а 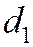- расстояние от той же точки до директрисы 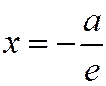, соответствующей фокусу .

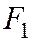Доказательство достаточности.

Возьмем каноническое уравнение эллипса, где a > b. Рассмотрим, например, фокус 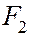этого эллипса и соответствующую ему директрису .

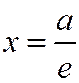Пусть М(х, у) такая точка, что

,

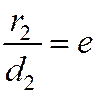где 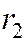- расстояние от точки М до фокус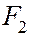а , а 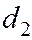- расстояние от точки М до директрисы .

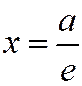Докажем, что точка М(х, у) лежит на эллипсе.

В самом деле, т.к.

; ,

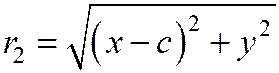то из соотношения

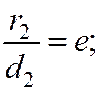или ,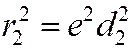

находим: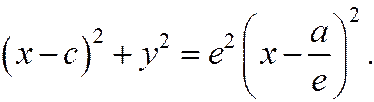

Упрощая это уравнение, получим 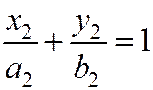. А это означает, что точка М(х, у) ежит на эллипсе.

Расстояние m от фокуса эллипса до его директрисы равно

,

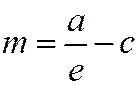а эксцентриситет определяется формулой:

.

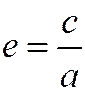Из этих соотношений находим .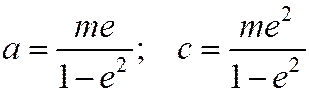

Отсюда следует, что если на плоскости задана произвольно точка 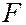, прямая, не проходящая через эту точку 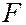(отстоящая от точки 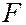на расстоянии 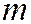) и задано произвольное положительное число е, меньшее 1, то существует эллипс, для которого точка 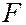- фокус, заданная прямая – директриса, а е- эксцентриситет. Центр этого эллипса находится на расстоянии

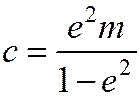
от точки 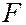(по одну сторону с точкой 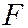от данной прямой), а большая полуось

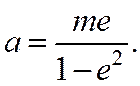
Отсюда и из только что доказанной теоремы следует, что эллипс можно определить как геометрическое место точек, для каждой из которых отношение расстояния от данной точки 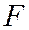к расстоянию до данной прямой 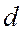, не проходящей через точку 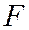, равно данному положительному числу, меньшему 1.

Исключением является окружность, которая данным свойством не обладает.