Сравнения любой степени по составному модулю.
Теорема
Если m1, m2, … , mk – попарно простые числа, то сравнение
f(x)≡0(mod m1·m2·…·mk) *
равносильно системе
 ** ,
** ,
причем, если первое сравнение имеет T1 решений по модулю m1, второе – T2 решений модулю m2, …, k-е сравнение имеет Tk решений по модулю mk, то исходное сравнение будет иметь T=T1·T2·…·Tk решений по модулю m1·m2·…·mk.
Доказательство:
Равносильность сравнения и системы очевидна и следует из свойств 12 и 13 сравнений.
Утверждение о количестве решений следует из того, что каждое сравнение
f(x)≡0(mod ms) ***
выполняется тогда и только тогда, когда выполняется одно из Ts сравнений вида x≡bs(mod ms) (где bs пробегает вычеты решений сравнения ***). Причем возможно всего T=T1·T2·…·Tk различных комбинаций вида x≡b1(mod m1), x≡b2(mod m2),…, x≡bk(mod mk), которые приводят (по китайской теореме об остатках) к различным классам вычетов по модулю m1·m2·…·mk.
□
Из доказанной теоремы следует, что решение сравнения вида 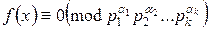 сводится к решению сравнений вида
сводится к решению сравнений вида 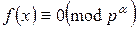 .
.
А решение сравнение вида f(x)≡0(mod pα) может быть найдено, если известно решение сравнения f(x)≡0(mod p). Покажем это.
Пусть x≡x1(mod p) – решение сравнения f(x)≡0(mod p). Тогда x можно представить в виде
x=x1+pt1, где 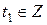 .
.
Подставляя такое x в сравнение f(x)≡0(mod p2) и применяя формулу Тейлора (учитывая, что f(x) – многочлен, x1 – целое число, поэтому  ), получаем
), получаем
f(x1)+pt1f '(x1)≡0(mod p2).
Поскольку f(x1)≡0(mod p), то p\f(x1), а значит можно сократить в получившемся выражении на p правую, левую части и модуль. Получим:
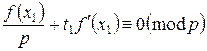
Если f '(x1) не делится на р, то данное сравнение имеет одно решение:
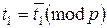 (т.е.
(т.е. 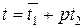 )
) 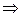
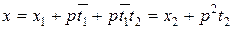
Подставляя полученное x в сравнение f(x)≡0(mod p3), имеем
f(x2)+p2t2f '(x2)≡0(mod p3),
откуда, сократив правую, левую части и модуль на p2 , получим
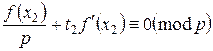
[Здесь f '(x2) не может быть кратно р, если f '(x1) не кратно p, т.к. x2≡x1(mod p), а значит, f '(x2) ≡ f '(x1) (mod p)]
Тогда сравнение имеет одно решение 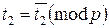 , или, что то же самое,
, или, что то же самое, 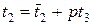 , откуда получаем решение по модулю p3 : x=x3+p3t3.
, откуда получаем решение по модулю p3 : x=x3+p3t3.
Продолжим этот процесс до тех пор, пока не будет решено сравнение по модулю pα. Итак, по данному решению сравнения f(x)≡0(mod p) можно найти решение сравнения f(x)≡0(mod pα).
Пример:
Требуется решить сравнение x3+9x—1≡0 (mod 125).
Известно, что сравнение x3+9x—1≡0 (mod 5) имеет одно решение:
x≡2(mod 5), или x=2+5t1.
Поскольку модуль «5» небольшой, а общих подходов к сравнениям высоких степеней мы пока не знаем, то этот корень нашли простым перебором, попутно убедившись в его единственности.
Подставим получившееся x в сравнение по модулю 25:
(2+5t1)3+9(2+5t1)—1≡0 (mod 25).
Решим это сравнение.
8+4·5t1+2·(5t1)2+(5t1)3+18+9·5t1—1≡0 (mod 25)
25+13·5t1+25·(5t13+2 t12) ≡0 (mod 25)
13·5t1≡0 (mod 25)
13t1≡0 (mod 5)
t1≡0 (mod 5)
Или, что то же самое, t1=0+5t2, откуда решение по модулю 25 есть x=2+25t2. Подставим полученное x в сравнение по модулю 125:
(2+25t2)3+9(2+25t2)—1≡0 (mod 125)
Решим это сравнение.
8+4·25t2+2·(25t2)2+(25t1)3+18+9·25t1—1≡0 (mod 125)
25+13·25t2+625·(25t23+2t22) ≡0 (mod 125)
25+13·25t2≡0 (mod 125)
1+13t2≡0 (mod 5)
13t2≡—1 (mod 5)
3t2≡4 (mod 5)
Получили сравнение первой степени. Решим его. Отыщем 3-1(mod 5), для чего, как всегда, воспользуемся расширенным алгоритмом Евклида:
5=3+2
3=2+1
2=1+0
1=3—2=3—(5—3)=2·3—1·5.
2≡3-1(mod 5).
Тогда решением сравнения относительно t2 будет
t2≡2·4 (mod 5)
t2≡3 (mod 5)
Или, что то же самое, t2=3+5t3, откуда решение по модулю 125 есть x=2+25(3+5t3)=2+75+125t3=77+125t3, или, что то же самое,
x≡77 (mod 125).
Дата добавления: 2015-11-28; просмотров: 3422;
