Свойства функции распределения
1) значения функции распределения 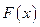 принадлежат отрезку
принадлежат отрезку 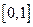 :
:
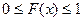 .
.
2) 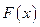 – неубывающая функция:
– неубывающая функция:
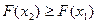 при
при 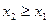 .
.
3) Вероятность того, что случайная величина примет значение, заключенное в интервале 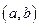 , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале:
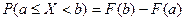 .
.
4) На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице:
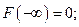
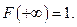
5) Вероятность того, что непрерывная случайная величина 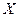 примет одно определенное значение, равна нулю.
примет одно определенное значение, равна нулю.
Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.
Определение.Плотностью распределения вероятностей непрерывной случайной величины 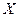 называется функция
называется функция 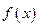 – первая производная от её функции распределения
– первая производная от её функции распределения 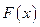 :
:
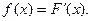
Плотность распределения также называют дифференциальной функцией.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
Определение.Случайная величина Х называется непрерывной, если ее функция распределения 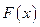 непрерывна на всей оси
непрерывна на всей оси 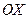 , а плотность распределения
, а плотность распределения 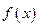 существует везде, за исключением может быть, конечного числа точек.
существует везде, за исключением может быть, конечного числа точек.
Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу 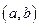 , равна определенному интегралу от плотности распределения, взятому в пределах от a до b:
, равна определенному интегралу от плотности распределения, взятому в пределах от a до b:
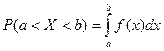 .
.
Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше.
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу 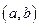 , равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения
, равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения 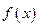 и прямыми
и прямыми 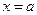 и
и 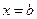 .
.
Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:
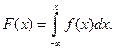
Дата добавления: 2015-11-28; просмотров: 621;
