Уравнений первого порядка
Линия  , являющаяся графиком функции, определяющей некоторое решение дифференциального уравнения, называется интегральной кривой уравнения
, являющаяся графиком функции, определяющей некоторое решение дифференциального уравнения, называется интегральной кривой уравнения 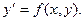
Производная 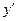 называется угловым коэффициентом касательной к интегральной кривой.
называется угловым коэффициентом касательной к интегральной кривой.
В любой точке 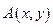 интегральной кривой этот угловой коэффициент касательной может быть найден до решения дифференциального уравнения.
интегральной кривой этот угловой коэффициент касательной может быть найден до решения дифференциального уравнения.
Так как касательная указывает направление интегральной кривой до ее непосредственного построения, то при условии непрерывности функции 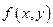 и непрерывного перемещения точки А можно наглядно изобразить так называемое поле направлений кривых, которые получаются в результате интегрирования дифференциального уравнения, т.е. представляют собой его общее решение.
и непрерывного перемещения точки А можно наглядно изобразить так называемое поле направлений кривых, которые получаются в результате интегрирования дифференциального уравнения, т.е. представляют собой его общее решение.
Определение. Множество касательных в каждой точке рассматриваемой области называется полем направлений.
Приведём следующее геометрическое истолкование дифференциального уравнения.
1) Задать дифференциальное уравнение первого порядка – означает задать поле направлений.
2) Решить или проинтегрировать дифференциальное уравнение означает найти всевозможные кривые, у которых направление касательных в каждой точке совпадает с полем направлений.
Определение. Линии равного наклона в поле направлений называются изоклинами.
8.3 Дифференциальные уравнения высших порядков
Дата добавления: 2015-11-28; просмотров: 741;
