Свойства числовых рядов
Числовые ряды
Основные определения
Определение. Пусть 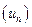 - произвольная числовая последовательность. Формальное выражение вида
- произвольная числовая последовательность. Формальное выражение вида
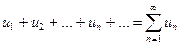
называется числовым рядом. Числа 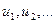 называются членами ряда, а
называются членами ряда, а 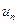 – общим членом ряда.
– общим членом ряда.
Определение. Суммы 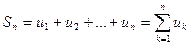 ,
, 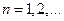 называются частичными суммами ряда.
называются частичными суммами ряда.
Определение. Ряд 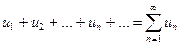 называется сходящимся, если существует конечный предел
называется сходящимся, если существует конечный предел 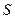 последовательности
последовательности 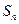
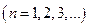 его частичных сумм. При этом число
его частичных сумм. При этом число 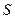 называется суммой ряда:
называется суммой ряда:
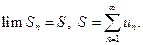
Определение. Если последовательность частичных сумм 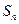
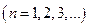 ряда
ряда 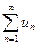 не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся.
не имеет предела, или имеет бесконечный предел, то ряд называется расходящимся.
Свойства числовых рядов
1) Сходимость или расходимость ряда не нарушится, если отбросить или добавить произвольное конечное число членов ряда.
2) Рассмотрим два ряда 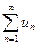 и
и 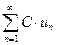 , где С – постоянное число.
, где С – постоянное число.
Теорема. Если ряд 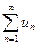 сходится и имеет сумму равную S, то ряд
сходится и имеет сумму равную S, то ряд 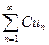 также сходится, и имеет сумму равную
также сходится, и имеет сумму равную 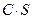
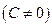 .
.
3) Рассмотрим два ряда 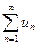 и
и 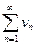 . Суммой (разностью) этих рядов называется ряд
. Суммой (разностью) этих рядов называется ряд 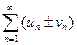 , где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
, где элементы получены в результате сложения (вычитания) исходных элементов с одинаковыми номерами.
Теорема. Если ряды 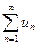 и
и 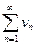 сходятся и их суммы равны соответственно
сходятся и их суммы равны соответственно 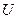 и
и 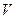 , то ряд
, то ряд 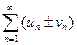 тоже сходится и его сумма равна
тоже сходится и его сумма равна 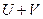 .
.
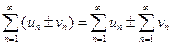
Сумма (разность) двух сходящихся рядов также является сходящимся рядом.
Сумма сходящегося и расходящегося рядов является расходящимся рядом.
О сумме двух расходящихся рядов общего утверждения сделать нельзя.
При изучении рядов решают в основном две задачи: исследование на сходимость и нахождение суммы ряда.
Дата добавления: 2015-11-28; просмотров: 503;
