Законы идеальных газов
Содержание и метод термодинамики
Термодинамика — наука, изучающая самые разнообразные явления природы, сопровождающиеся передачей или превращением энергии в различных физических, химических, механических и других процессах.
Как наука, термодинамика сложилась в середине XIX века в связи с развитием и использованием тепловых машин. Поэтому основное содержание термодинамики прошлого столетия — изучение свойств газов и паров, исследование циклов тепловых машин с точки зрения повышения их к.п.д.. В силу этого основным методом термодинамики XIX века был метод круговых процессов. С этим этапом развития термодинамики связаны имена ее основателей: С. Карно, Б. Клапейрона, Р. Майера, Д. Джоуля, В. Томпсона (Кельвина), Р. Клаузиуса, Г. И. Гесса и др.
В XX веке наиболее актуальной задачей становится разработка теории истечения паров и газов в связи с развитием паровых турбин. Исследуются термодинамические свойства паров, жидкостей, твердых тел. Появляются десятки уравнений состояния вещества, изучаются фазовые равновесия и фазовые превращения, ведется исследование электрических, магнитных процессов, лучистой энергии, химических реакций, термодинамики реальных тел. Указанные области исследований термодинамики связаны с именами Ван-дер-Ваальса, Дюгема, Г. Кирхгофа, М. Планка, Л. Больцмана, В. Гиббса, Н. С. Курнакова, М. П. Вукаловича, Н. И. Белоконя, В. А. Кириллина и др. ученых.
В настоящее время развитие термодинамики идет в области изучения реальных тел (сжатых газов, жидкостей, твердых тел), исследования дисперсных систем, химических процессов в сплавах и растворах, оптических явлений и космических процессов, развивается термодинамика биологических процессов и т. д.
Термодинамика — наука дедуктивная, определяющая свое содержание на базе математического развития нескольких исходных экспериментально установленных физических истин или законов, которые и носят поэтому название начал термодинамики.
Основу всех построений термодинамики составляют следующие ее постулаты:
I постулат: Энергия изолированной системы сохраняет неизменную величину при всех изменениях, происходящих внутри данной системы. Невозможно построить двигатель, который мог бы совершать работу без заимствования энергии извне. Этот постулат является частным случаем общего абсолютного закона природы — закона сохранения и превращения энергии, а также основанием первого начала термодинамики.
II постулат: Между телами и элементами тел, не находящимися в тепловом равновесии, невозможен одновременный самопроизвольный переход теплоты от тел более нагретых к телам менее нагретым и обратно. Невозможно одновременное превращение (полное) теплоты в работу и работы — в теплоту. Этот постулат является основанием второго начала термостатики — закона, утверждающего существование абсолютной температуры и энтропии тела и системы тел.
III постулат: Теплота самопроизвольно переходит от тел более нагретых к телам менее нагретым. Температура является единственной функцией состояния, определяющей направление самопроизвольных процессов. Этот постулат положен в основу второго начала термодинамики — принципа возрастания энтропии и указывает на неизменный рост энтропии изолированной системы.
Основные понятия термодинамики
Состояние любого вещества принято характеризовать величинами, которые в термодинамике называются параметрами состояния. Наиболее распространенные параметры состояния — плотность или удельный объем тела, давление, температура. Кроме этого, в термодинамике широко пользуются такими понятиями, как работа, теплота, масса, сила и т. д.
Масса тела (М) характеризует свойство его инертности, т. е. свойство тела сохранять приобретенное движение или состояние покоя. Массу тела определяют взвешиванием его на рычажных весах. Единица измерения массы — 1 кг.
Сила (F) — это векторная величина, равная произведению постоянной массы на ускорение, которое сообщает этой массе рассматриваемая сила. Единица измерения любой силы — ньютон (Н). Силу определяют с помощью пружинных весов.
Истинный вес (F) — это сила, равная произведению массы этого тела на истинное ускорение притяжения, действующее на эту массу:
F=M×g. (3.1)
Стандартный вес (G) — это вес тела при некотором принятом (стандартном) ускорении притяжения gn и определяется как результат взвешивания на рычажных весах при сопоставлении с эталоном (гирей):
G=gn×M0, (3.2)
где M0 — масса в состоянии покоя,
gn=9,8×м/с2 [МКСС], gn=1 [СИ].
Удельный объем (υ) — это величина отношения объема тела к его стандартному весу:
υ=V/G=V/M0 (м3/кг). (3.3)
Удельный вес (g) — это отношение стандартного веса тела к его объему:
g=G/V (кг/м3); g=1/υ. (3.4)
Плотность(ρ) — есть масса единицы объема:
ρ=M/V [кг/м3]; ρ=1/υ. (3.5)
Соотношение удельного веса и плотности равно стандартному ускорению притяжения γ/ρ=G/V×V/M=gn. В системе СИ они совпадают, т. к. gn=1.
Часто в термодинамике используются понятия относительной плотности или относительного удельного веса d=D=g/g0=r/r0. Это отношение удельного веса или плотности рассматриваемого вещества (g, r) к удельному весу или плотности стандартного вещества (g0, r0) в определенных физических условиях. В качестве стандартного вещества обычно берется вода при t=+4°С и р=760 мм рт. ст. или воздух при 0°С и р=760 мм рт. ст.
Моль — количество вещества, стандартный вес которого численно равен его молекулярной массе (μ).
Удельный мольный вес ( 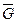 ) — количество вещества в химии, равное отношению стандартного веса к его молекулярному весу:
) — количество вещества в химии, равное отношению стандартного веса к его молекулярному весу:
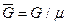 . (3.6)
. (3.6)
Удельный мольный объем 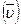 — это объем моля вещества, который равен отношению объема тела к количеству вещества в молях:
— это объем моля вещества, который равен отношению объема тела к количеству вещества в молях:
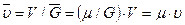 . (3.7)
. (3.7)
Давление (Р) — это предел отношения нормальной составляющей силы к площади, на которую действует эта сила (рис. 3.1):
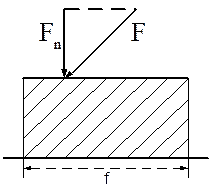
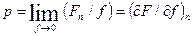 . (3.8)
. (3.8)
Различают два вида приборов для измерения давления: приборы для измерения абсолютного давления Рабс и приборы манометрического типа для измерения избыточного или манометрического давления (Рман=Ризб) (рис. 3.2). Абсолютное давление
Рис. 3.1. К определению давления Рабс=Рман+В0=В0±gF×H, (3.9)
где В0 — барометрическое давление.
Единица измерения давления в системе СИ — паскаль [Па] = [Н/м2]. Внесистемные единицы измерения: 1[кг/см2] = 1[ат] = 104[кг/м2] =104. 9,8 » 105[Н/м2] = 10 м вод. ст. = 735,66 мм рт. ст.
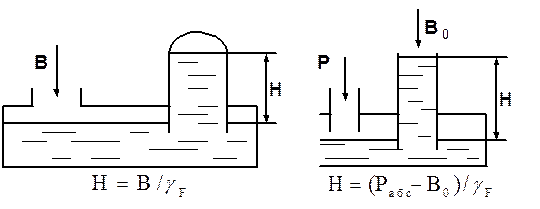
Рис. 3.2. К определению абсолютного и манометрического давлений
Температура — есть единственный параметр состояния вещества, определяющий направление самопроизвольного теплообмена между телами. Для любого тела существует функциональная зависимость между температурой и остальными параметрами, характеризующими состояние вещества.
В настоящее время используют различные температурные шкалы: Цельсия, Фаренгейта, Реомюра, Ренкина. Наиболее употребительной является шкала Цельсия, в которой интервал температур от точки плавления льда до точки кипения воды при атмосферном давлении разбит на 100 равных частей, называемых градусами (˚С). Особо важную роль в термодинамике играет термодинамическая шкала температур. Нуль этой шкалы называют абсолютным нулем, а деление шкалы — кельвинами (К). Связь между шкалой Кельвина (Т) и Цельсия (t) устанавливается соотношением: Т=t+273,16.
Внутренней энергией тела (U) называется полный запас энергии внутреннего состояния тела, изменяющийся в процессах теплообмена и выполнения работы, определяемый значением его внутреннего состояния. U измеряется в джоулях (Дж), удельная внутренняя энергия u — в (Дж/кг). Внутренняя энергия определяется в зависимости от температуры и деформационных координат системы: U=U(t, x1, x2, …, xn).
Для простых тел внутренняя энергия — это функция только 2-х переменных, например, t и υ (х1=υ). Внутренняя энергия является функцией состояния системы, поэтому дифференциал внутренней энергии dU есть полный дифференциал функции состояния:
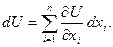 (3.10)
(3.10)
Это сумма кинетической и потенциальной энергий всех микрочастиц, составляющих тело.
Потенциальная функция (PV) характеризует энергию внешнего положения системы, измеряется в джоулях (Дж) или, если записать для единицы массы (т. е. вместо полного объема (V) взять удельный (υ)), — Рυ (Дж/кг). Потенциальная функция по физическому смыслу представляет собой потенциальную энергию связи данного тела с окружающей средой при осуществлении этой связи исключительно через внешнее давление, т. е. это работа, затраченная для введения тела объемом V (υ) во внешнюю среду с давлением Р, одинаковым во всех точках этой среды.
ЭнтальпияН=U+PV (Дж) или для единицы массы h=u+Pυ (Дж/кг) — полная энергия тела с учетом энергии внешнего (PV) и внутреннего (U) состояния системы. Устаревшее название энтальпии — теплосодержание.
Термодинамическая система или тело — это такая равновесная система, которая способна обмениваться с другими телами энергией и веществом.
Открытая термодинамическая система может обмениваться веществом с другими системами, а закрытая— не может.
Изолированная термодинамическая система — та, которая не может обмениваться энергией и веществом с другими системами.
Термодинамическое равновесие — такое состояние теплового, химического равновесия тела или системы, которое может сохраняться без внешнего воздействия как угодно долго. Характеризуется равенством параметров системы. Если хотя бы один из параметров системы меняется, то изменяется и состояние системы или, как принято говорить, осуществляется термодинамический процесс, представляющий собой непрерывную последовательность равновесных состояний.
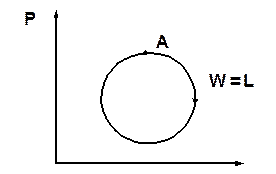 Обратимый процесс — это процесс, который в условиях изолированной системы, т. е. без внешнего воздействия, допускает возврат системы в исходное состояние. Если направления прямого и обратного процессов совпадают, то процесс называют конфигуративным.
Обратимый процесс — это процесс, который в условиях изолированной системы, т. е. без внешнего воздействия, допускает возврат системы в исходное состояние. Если направления прямого и обратного процессов совпадают, то процесс называют конфигуративным.
Круговой процес (цикл) хар-
актеризуется возвратом рабочего тела в исходное состояние (рис. 3.3). В этих процессах 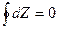 , где Z=P, υ, t, U… и т. д., т. е. дифференциалы функций состояния — это полные дифференциалы кругового процесса. Такие процессы
, где Z=P, υ, t, U… и т. д., т. е. дифференциалы функций состояния — это полные дифференциалы кругового процесса. Такие процессы
Рис. 3.3. Круговой процесс положены в основу тепловых машин.
Теплотаесть энергия, не связанная с переносом вещества и совершением работы.
Теплообмен — форма передачи энергии от одних тел к другим путем теплопроводности, конвекции и излучения. Теплообмен между телами осуществляется только в условиях, когда тела имеют разную температуру.
Тело или система тел содержит только внутреннюю энергию. Количество теплоты, получаемое телом, зависит от вида процесса, от пути, по которому система переходит из одного состояния в другое. Поэтому элементарные количества теплоты рассматриваются как бесконечно малые величины, не являющиеся полными дифференциалами: δQ ― элементарное количество теплоты, полученное телом; δq — элементарное количество теплоты, отнесенное к единице массы вещества.
δq=δQ/G. (3.11)
Знак δ указывает, что δQ и δq — неполный дифференциал. Количественные выражения теплоты имеют одинаковую единицу измерения с внутренней энергией — Дж и Дж/кг.
Работа.
Количественное выражение элементарной работы δL в общем виде определяется как произведение проекции Fs силы F на элементарное перемещение точки приложения силы (рис. 3.4).
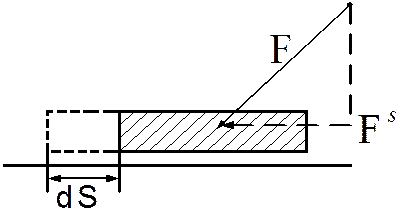
Рис. 3.4. Определение элементарной работы
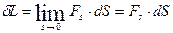 . (3.12)
. (3.12)
Работа есть эффект перемещения силы, она зависит от вида процесса. Следовательно, выражение элементарной работы не является полным дифференциалом и знак δ как общий символ бесконечно малых величин указывает на это.
Рассмотрим работу в цилиндре поршневой машины. Элементарная работа сжимаемых тел определяется в зависимости от давления и изменения объема:
Fs=P×f; dS=1/f×dV;
dL=Fs×dS=P×f×(1/f)×dV=P×dV;
dL=P×dV. (3.13)
Работу изменения объема называют термодинамической работой(рис. 3.5). Эта работа в P-V координатах определяется площадью, ограниченной линией процесса и координатами точек начала и конца процесса. Работа считается положительной (L1,2>0), если система совершает ее над внешними телами, т. е. при dV>0, и отрицательной (L1,2<0), если внешние тела совершают работу над системой, т. е. при dV<0 (рис. 3.6).
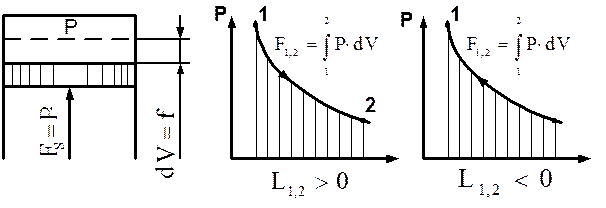
Рис. 3.5. Определение термодинамической Рис. 3.6. Графическое изображение
работы термодинамической работы
Часто в термодинамике оперируют понятием удельной термодина-мической работы, т. е. работы изменения объема, отнесенной к 1 кг:
dl=1/G×dL=1/G×P×dV=P×du,
l1,2= 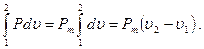 (3.14)
(3.14)
Интегральное определение полной L1,2 и удельной l1,2 термодинамической работы возможно лишь при наличии уравнений связи между давлением и объемом: j (P, V)=0; j (P, υ)=0.
Эффективная работа реального процесса (dL*, dl*) определяется как разность между обратимой работой изменения объема (dL, dl) и работой необратимых потерь (dL**, dl**).
dL*=dL-dL**; dl*=dl-dl**. (3.15)
Работа, потерянная в необратимых процессах, превращается в теплоту внутреннего теплообмена.

Рис. 3.7. К определению потенциальной работы
Потенциальная работа (W1,2) — работа по обратимому перемещению жидкостей, паров и газов из области одного давления Р1 в область другого давления Р2. Слагаемые потенциальной работы по перемещению газа из области давления Р1 в область давления Р2 изображены на схеме 3.7.
Основные условные слагаемые потенциальной работы — это наполнение LI, расширение (сжатие) LII и выталкивание LIII.
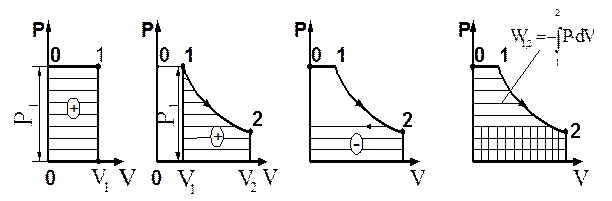
Рис. 3.8. Этапы совершения потенциальной работы
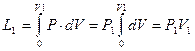 ; (3.16)
; (3.16)
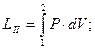
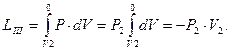
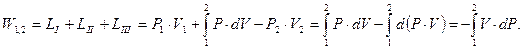
dW = -V×dP. (3.17)
Элементарная удельная потенциальная работа:
dw = (1/G)×dW = -u×dP. (3.18)
Потенциальная работа имеет положительный знак при перемещении жидкости или газа из области большего давления в область меньшего давления (Р1>Р2) и наоборот, т. е. при расширении положительна, при сжатии — отрицательна. Как и термодинамическая работа, потенциальная измеряется площадью в P-V координатах (рис. 3.8).
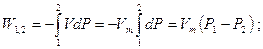 (3.19)
(3.19)
аналогично, для удельной потенциальной работы:
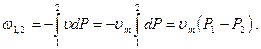 (3.20)
(3.20)
При вычислении интегральной величины потенциальной работы, как и при вычислении интегральной термодинамической работы, необходимо иметь уравнение процесса изменения состояния вещества j (P, V)=0, или j1 (P, u)=0 для удельной потенциальной работы.
Потенциальная работа dW, dw — это сумма эффективной работы dW* и работы необходимых потерь dW**.
dW=δW*+δW**; соответственно, dw=dw*+dw**.
Потенциальная работа необратимых потерь dW* превращается в теплоту внутреннего теплообмена. Эффективная потенциальная работа dW*=dW-dW** непосредственно передается телам внешней системы dLc* и используется для изменения внутренней энергии внешнего положения рабочего тела dEcz.
dW*=dEc*+dEcz. (3.21)
Газовые смеси
Смесь представляет собой систему тел, химически не взаимодействующих между собой. Структура отдельных компонентов смеси в процессах смесеобразования и стабилизации смеси не изменяется.
Различают два основных способа задания смеси: весовыми (массовыми) и мольными (объемными) концентрациями.
Весовая (массовая) концентрация смеси mi представляет собой отношение стандартного веса или массы компонента к стандартному весу или массе всей смеси:
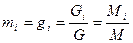 ;
; 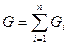 ;
; 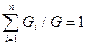 .
.
Мольная (объемная) концентрация ri есть величина отношения количества молей компонентов 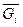 к количеству молей смеси:
к количеству молей смеси:
ri= 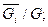
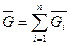 ;
; 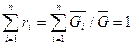 .
.
Количество молей компонента 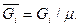
Молекулярный (кажущийся) вес смеси равен в зависимости от способа задания смеси:
через объемные доли:
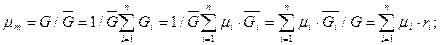 (3.22)
(3.22)
через массовые доли:
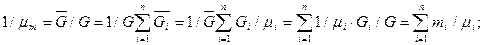 (3.23)
(3.23)
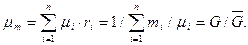 (3.24)
(3.24)
Пересчет весовых и объемных концентраций можно осуществить из уравнения:
mi/ri=mi/mm; mi/ri=mi/mm=Rm/Ri,
где Rm — газовая постоянная смеси Rm= 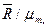
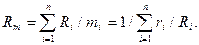
Давление смеси представляет собой сумму давлений компонентов, входящих в смесь 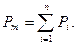 Давление одного компонента устанавливается на основании закона Дальтона (закона диффузионного равновесия) Pi=Pm×ri, где Pi — парциальное давление газов, входящих в смесь.
Давление одного компонента устанавливается на основании закона Дальтона (закона диффузионного равновесия) Pi=Pm×ri, где Pi — парциальное давление газов, входящих в смесь.
Законы идеальных газов
Идеальным газом является газ, подчиняющийся уравнению Клапейрона при любых плотностях и давлениях.
1. Закон Бойля — Мариотта(1622 г.). Если температура газа постоянна, то давление газа и его удельный объем связаны зависимостью:
P1u1=P2u2=idem, или u2/u1=P1/P2. (3.25)
2. Закон Гей — Люссака(1802 г.). При постоянном давлении объем газа при нагревании изменяется прямо пропорционально повышению температуры:
u=u0(1+at), (3.26)
где u — удельный объем газа при температуре t°C,
u0 — удельный объем газа при температуре t=0°С,
a — температурный коэффициент объемного расширения идеальных газов при t=0°C одинаковый для различных газов и сохраняющий одно и то же значение: a=1/273,16=0,00366 1/°С.
3. Закон (уравнение) Клапейрона (1834 г.). Сопоставление законов Бойля — Мариотта и Гей — Люссака приводит к уравнению состояния идеальных газов:
u=u0(1+at)=const/P=a×const/P(1/a+t);
1/a+t=T; a×const=R; T=273,16+t°C;
Pu=RT; PV=GRT=MRT, (3.27)
где R — газовая постоянная идеального газа. Представляет собой удельную работу газа в изобарном процессе (P — idem) при изменении температуры газа на 1°С.
4. Закон Авогадро (1811 г.). Объем киломоля идеального газа ( 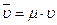 ) не зависит от его природы и вполне определяется параметрами физического состояния газа (P, t):
) не зависит от его природы и вполне определяется параметрами физического состояния газа (P, t):
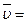 ƒ(P, t).
ƒ(P, t).
Объем 1 кмоля идеального газа в нормальных физических условиях (температура 0°С, давление 101,325 кПа)
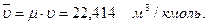
Уравнение Клапейрона для одного кмоля идеального газа имеет вид
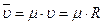 ,
,
тогда mR не зависит от природы газа и в силу этого называется универсальной газовой постоянной:
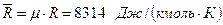 . (3.28)
. (3.28)
Удельные газовые постоянные газов R определяются по значению их молярной массы:
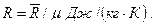 (3.29)
(3.29)
Таким образом, уравнение состояния идеального газа (уравнение Клапейрона) может быть записано в следующих видах:
для 1 кг газа Pu=RT,
для G кг газа PV=GRT,
для 1 кмоля газа (уравнение Клапейрона — Менделеева)
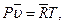
для 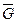 кмолей газа
кмолей газа 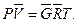 (3.30)
(3.30)
Дата добавления: 2016-01-20; просмотров: 913;
