Примеры схемной реализации логических функций на логических элементах

Синтез комбинационных дискретных устройств

Задачей синтеза любого ДУ является получение структуры этого устройства из минимального числа элементов, реализующей заданный в словесной форма алгоритм его функционирования.

Процесс синтеза ДУ разбивается на три больших этапа:

этап абстрактного синтеза;

этап структурного синтеза;

этап выбора элементов для построения ДУ.

На этапе абстрактного синтеза решается задача представления алгоритма функционирования ДУ в какой-либо стандартной форме, удобной для получения на этапе структурного синтеза структурных формул. На этом этапе синтеза тип элементов, из которых будет строиться ДУ, и их физическая природа, как правило, не учитыва­ются.

Этап структурного синтеза включает описание процесса функ­ционирования ДУ на языке структурных формул, их минимизацию и построение на этой основе структурной схемы устройства.

Рассмотрим порядок синтеза комбинационного ДУ.

1. Этап абстрактного синтеза:

- формулирование условий работы ДУ в словесной форме;

- представление условий работы ДУ в стандартной форме.

2. Этап структурного синтеза:

- составле6ние первоначальных структурных формул;

- минимизация первоначальныхструктурных формул;

- составление структурной (функциональной) схемы ДУ.

Выбора элементов для построения ДУ.

Примеры схемной реализации логических функций на логических элементах

Условия работы ДУ могут формулироваться словесно или записью. Они должны точно отражать специфику работы ДУ, четко определять его рабочие, запрещенные и условные состояния.

Рассмотрим методику синтеза комбинационного ДУ на примере.

Необходимо произвести синтез ДУ, имеющего три воспринимающих (А,В,С) и один исполнительные (Z) элемент. Цепь исполнительного элемента должна быть замкнута при следующих условиях:

включен элемент А или В;

одновременно включены элементы А и В;

включены все три воспринимающих элемента.

Цепь исполнительного элемента должна быть разомкнута при сле­дующих условиях:

выключены все воспринимающие элементы;

одновременно включены элементы В и С.

Остальные комбинации состояний воспринимающих элементов либо невозможны, либо состояние исполнительного элемента в этих слу­чаях нам безразличны.

По сформулированным условиям работы ДУ составля­ется таблица состояний, которая является стандартной формой запи­си условий работы. Таблица состояний составляется в следующей последовательности:

1. По числу входов (воспринимающих элементов) определяется количество возможных комбинаций состояний входов.

2. Все комбинации состояний входов в виде двоичных чисел (включенному состоянию воспринимающего элемента соответствует I, выключенному - 0) в возрастающем порядке записываются в таблицу.

3. В столбце исполнительного элемента напротив соответствую­щих комбинаций состояний входов отмечаются рабочие (I), запрещен­ные (0) и условные ( ) состояния ДУ.

Для заданных условий работы ДУ получим следующую таблицу состояний:

Таблица состояний

	А	В	С	Z

На основании таблицы состояний составляются первоначальные структурные формулы (могут составляться в различных формах). Для заданных условий работы структурная формула управляющей функции имеет вид:

в сднФ -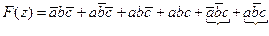

Для минимизации первоначальных структурных формул в зависи­мости от их формы записи могут использоваться различные методы. Структурные формулы в СДНФ минимизируются е помощью законов и соотношений алгебры логики и матрицы Карно.

Некоторые из этих законов:

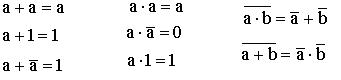
Минимизируем полученную структурную формулу в СДНФ с помощью законов и соотношений алгебры логики.

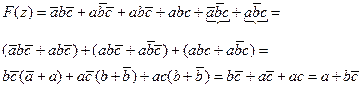
В зависимости от назначения и условий эксплуатации ДУ может

быть выполнено на контактных иди бесконтактных элементах. Основой для построения принципиальной электрической схемы ДУ на контакт­ных элементах является его структурная схема, а для построения принципиальной электрической схемы на бесконтактных элементах - функциональная схема. На основании минимизированной структурной формулы построим функциональную схему синтезируемого ДУ.

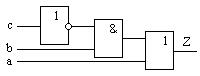
Рис. . функциональная схема ДУ