Расчет переходных процессов при несимметричных КЗ
Для расчета несимметричного КЗ пользуются методом симметрических составляющих.
Основные положения метода
1) Каждый вектор несимметричной системы может быть представлен суммой 3-ех симметричных векторов – прямой, обратной и нулевой последовательности.
2) В трёхфазной цепи в месте КЗ, наряду с напряжением прямой последовательности, возникает напряжение обратной и нулевой последовательностей. В ветвях схемы вместе с токами прямой последовательности начинают циркулировать токи обратной и нулевой последовательностей.
3) В симметричных электрических системах токи и напряжения схем отдельных последовательностей могут рассматриваться независимо друг от друга и быть связаны между собой Законами Ома и Киргофа.

Из условия разложения можно записать систему:
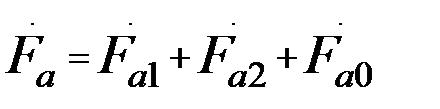
 (39.1)
(39.1)
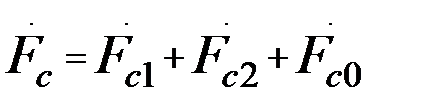
Введение специального оператора фазы «а»позволяет вектора каждой симметричной системы выразить через какой-либо один вектор той же системы. Оператор фазы является вектором, модуль которого равен 1, а аргумент 120°. Умножить на «а» - это означает повернуть вектор на 120˚ против часовой стрелки. 
Основные свойства оператора фазы:
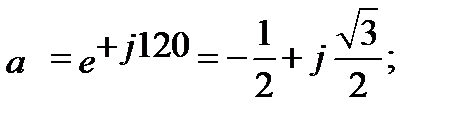
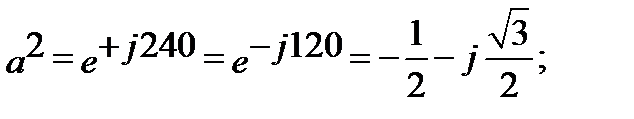

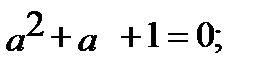
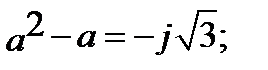
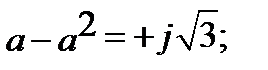
Если фазу «А»принять за основную, то систему (39.1) можно записать:
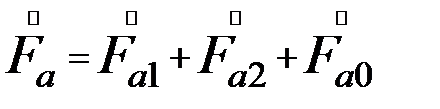
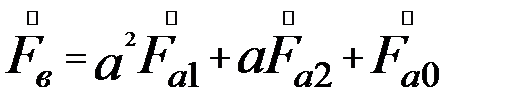 (39.2)
(39.2)
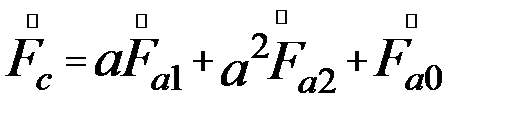
Совместное решение уравнений систем (39.1) и (39.2) дает систему (39.3), по которой можно определить все симметричные составляющие
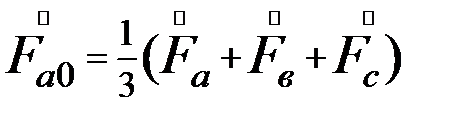
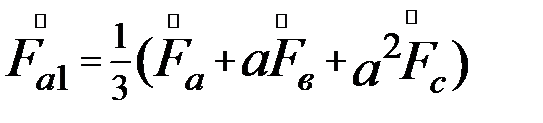 (39.3)
(39.3)
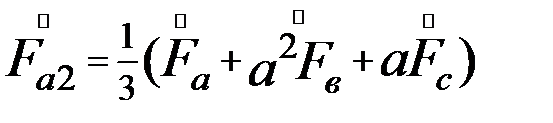
Дата добавления: 2016-01-20; просмотров: 943;
