Операторные реактивности синхронной машины

По аналогии с операторным сопротивлением 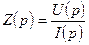операторная реактивность 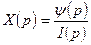является функцией, связывающей изображения для потокосцепления и тока.

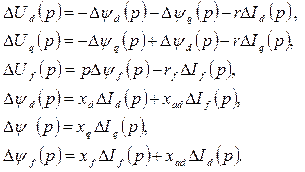
Из уравнения (3.7) можно выразить операторную реактивность поперечной оси:

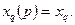
Операторную реактивность в продольной оси находим, используя уравнения (3.5) и (3.6):

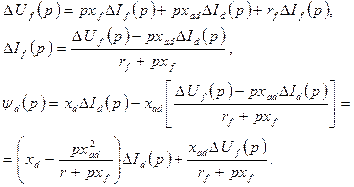
Второе слагаемое уравнения (3.9) не зависит от параметра 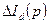и определяется только свойствами системы регулирования возбуждения. Поэтому операторная реактивность в продольной оси

.

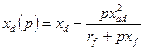Схемная интерпретация реактивности 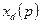будет более наглядной, если выполнить ряд преобразований. Учитывая, что синхронная реактивность статора в продольной оси имеет две составляющие: реактивность рассеяния и реактивность взаимной индукции 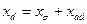(для обмотки возбуждения 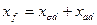), получим

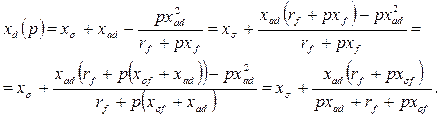
Второе слагаемое представляет собой эквивалентное сопротивление двух параллельных ветвей .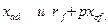

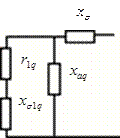
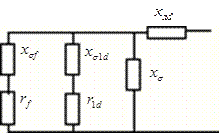
Аналогично можно определить операторные реактивности машины с демпферными обмотками. Схемы замещения, отвечающие этим реактивностям, приведены на рис. 3.1.

			б
		a

Рис. 3.1. Схемы замещения, определяющие операторные реактивности для машины с демпферными обмотками:

а - в продольной оси; б - в поперечной оси.