Элементы схем и их параметры
Пассивные элементы
К линейным пассивным элементам относятся: активное сопротивление, индуктивность и емкость.
Активное сопротивление (R) – идеализированный элемент, характеризующий потери энергии. К ним относят элементы, в которых происходят необратимые процессы превращения электрической (электромагнитной) энергии в другие виды энергии, например, в тепловую, механическую, световую и другие виды.
Величина сопротивления R является количественной мерой потерь электрической (электромагнитной) энергии. Единицей измерения сопротивления является Ом. На практике также широко используются дольные и кратные единицы сопротивления - от единиц микроом (1 мкОм = 10-6 Ом) до единиц гигаом
(1 ГОм = 109 Ом) и больше.
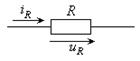
Электротехническое устройство, обладающее сопротивлением и по своим свойствам наиболее близкое к активному сопротивлению (идеализированному элементу), называется резистором. В схемах замещения активное сопротивление, как и резистор, изображают в виде прямоугольника с соотношением сторон 10 к 4 (Рис. 1.6). На принципиальных схемах такое условное графическое обозначение соответствует постоянному резистору.
|
| Рис. 1.6 – Условное графическое обозначение активного сопротивления |
Величину, обратную активному сопротивлению, называют активной проводимостью и обозначают Y. Единицей измерения проводимости является сименс (См).
Y = R – 1, См или Ом – 1.
На схемах проводимость обозначают так же, как и активное сопротивление.
Для линейных электрических цепей величина активного сопротивления постоянная (R = const). Линейность активного сопротивления означает, что его величина не зависит от протекающего тока и приложенного напряжения.
Ток iR и напряжение uR в R связаны линейной зависимостью:
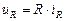 . (1.1)
. (1.1)
Скорость преобразования электрической энергии в активном сопротивлении характеризуется активной мощностью p. В общем случае ее определяют как производную по времени от рассеиваемой в R энергии w
p = dw / dt . (1.2)
Если напряжение uR и ток iR в активном сопротивлении известны, то мощность p находят как
p = uRiR. (1.3)
Учитывая, что 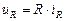 или
или 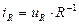 , можно также записать, что
, можно также записать, что
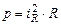 или p =
или p = 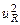 / R . (1.4)
/ R . (1.4)
Энергия W, которая выделилась в активном сопротивлении за время t, определяется как
W = 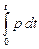 . (1.5)
. (1.5)
Для случая постоянного тока, когда напряжение UR и ток IR не изменяются во времени, что характерно для цепей постоянного тока, активная мощность P будет постоянной. Ее определяют по формулам:
P = UR ·IR , P = 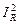 ·R или P =
·R или P = 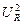 / R. (1.6)
/ R. (1.6)
Выделенная в активном сопротивлении R за время t энергия W постоянного тока определяется, с учетом (1.5) и (1.6), как
W = P t , W = 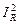 R t или P = [
R t или P = [ 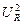 / R] t . (1.7)
/ R] t . (1.7)
Индуктивность (L) – это идеализированный элемент цепи (Рис 1.7), способный накапливать энергию магнитного поля. Индуктивность L ,как параметр цепи, измеряется в генри (Гн) и служит количественной мерой магнитного поля, создаваемого током i (1 Гн = 1 В·с / А). Близким по своим свойствам к индуктивности L элементом цепи является катушка индуктивности без ферромагнитного сердечника.
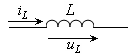
|
| Рис. 1.7 – Условное графическое обозначение индуктивности |
Величина индуктивности L элемента цепи, например, катушки индуктивности, определяется отношением потокосцепления самоиндукции ψ к току i вданном элементе
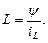 (1.8)
(1.8)
Потокосцеплением самоиндукции элемента цепи называют полный магнитный поток, созданный током iL в данном элементе. Например, если катушка состоит из w витков и все они пронизываются магнитным потоком Ф, созданным током этой катушки, то потокосцепление самоиндукции ψ = w Ф.
При изменении потокосцепления ψ в катушке согласно закону электромагнитной индукции возникает ЭДС самоиндукции eL. Она определяется как
eL 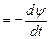 . (1.9)
. (1.9)
С учетом, что ψ = L iL (см. выражение 1.8), получим:
eL 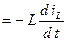 . (1.10)
. (1.10)
Из (1.10) следует, что ЭДС самоиндукции всегда направлена против изменения тока (правило Ленца) и определяется знаком производной тока.
Напряжение на индуктивности
uL = – eL 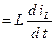 . (1.11)
. (1.11)
Энергия магнитного поля индуктивности при известном токе iL определяется как
WM = 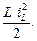 (1.12)
(1.12)
Для постоянного тока индуктивность никакого сопротивления не оказывает. В этом случае напряжение на индуктивности uL = 0, ток в индуктивности iL = IL , энергия магнитного поля
WM = 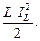 (1.13)
(1.13)
Индуктивность присуща любому реальному элементу электрической цепи, если в нем протекает ток, которому всегда сопутствует магнитное поле.
Емкость (С) – идеализированный элемент, накапливающий энергию в электрическом поле. Емкость, как и индуктивность, присутствует в любом реальном элементе электрической цепи, где имеется напряжение. Наиболее близким по своим свойствам к емкости С элементом цепи является конденсатор (Рис.1.8). Емкость, как параметр цепи, является количественной мерой электрического поля, создаваемого зарядами. Единица измерения емкости – фарад (Ф). 1Ф = 1Кл/В или 1Ф = 1А·с/В.
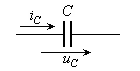 Рис. 1.8 - Условное
графическое обозначение
емкости
Рис. 1.8 - Условное
графическое обозначение
емкости
|
Накопленный в емкостном элементе заряд определяется величиной емкости С и напряжением 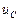 :
:
q = C 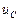 . (1.14)
. (1.14)
С учетом формулы (1.14) ток в емкости
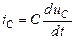 . (1.15)
. (1.15)
Энергия электрического поля линейной емкости C при напряжении 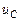 определяется формулой:
определяется формулой:
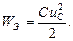 (1.16)
(1.16)
Емкостные элементы, как и индуктивные, в отличие от активного сопротивления, энергию цепи не расходуют. Они могут накапливать энергию, забирая ее из цепи, и отдавать обратно в цепь. Их реакция на воздействие в виде тока или напряжения в электрической цепи подобна реакции пружины на механическое воздействие в каком-либо механическом устройстве. В этой связи элементы L и С называют реактивными элементами.
Активные элементы
В электротехнике широко используются понятия идеализированных источников электрической энергии - идеального источника ЭДС и идеального источника тока.
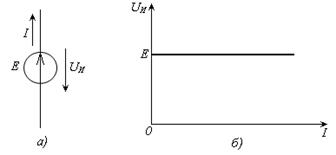
Идеальный источник ЭДС (или просто источник ЭДС) – это такой источник, у которого выходное напряжение не зависит от нагрузки (Рис. 1.9). Внешняя характеристика такого источника 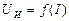 определяется выражением:
определяется выражением:
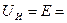 const .(1.17)
const .(1.17)
У источника ЭДС отсутствуют внутренние потери энергии. Внутреннее сопротивление у него отсутствует ( 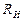 = 0).
= 0).
|
| Рис. 1.9 – Источник ЭДС: а) условное графическое изображение; б) внешняя характеристика |
Реальные источники электрической энергии (Рис. 1.10) обладают внутренним сопротивлением 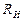 ≠ 0, что является причиной потерь энергии в самом источнике. Внешняя характеристика реального источника имеет наклон (Рис. 1.10, б) за счет падения напряжения на сопротивлении
≠ 0, что является причиной потерь энергии в самом источнике. Внешняя характеристика реального источника имеет наклон (Рис. 1.10, б) за счет падения напряжения на сопротивлении 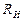 .
.
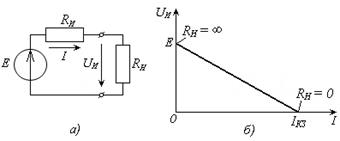
Рис. 1.10. – Реальный источник: а) схема источника с подключенной нагрузкой; б) внешняя характеристика
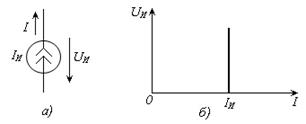
Идеальный источник тока (или просто источник тока) – идеализированный источник энергии, ток которого не зависит от напряжения на его зажимах ( то есть не зависит от нагрузки). Внешняя характеристика (Рис. 1.11) источника тока описывается выражением:
IИ = const. (1.18)
|
| Рис. 1.11 – Источник тока: а) условное графическое изображение; б) внешняя характеристика |
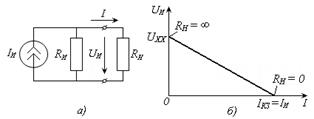
Любой реальный источник электрической энергии можно заменить эквивалентной схемой замещения с помощью источника тока, как показано на рис. 1.12.
|
| Рис. 1.12 – Реальный источник: а) схема источника с подключенной нагрузкой; б) внешняя характеристика |
Значение тока IИ можно определить расчетным путем, предположив 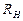 = 0. Сравнивая схемы замещения реального источника, приведенные на Рис 1.10, а) и на Рис. 1.12, а), можно заметить, что по отношению к нагрузке они равнозначны. Внешние характеристики для обеих схем одинаковы (см. Рис 1.10, б и Рис. 1.12, б).
= 0. Сравнивая схемы замещения реального источника, приведенные на Рис 1.10, а) и на Рис. 1.12, а), можно заметить, что по отношению к нагрузке они равнозначны. Внешние характеристики для обеих схем одинаковы (см. Рис 1.10, б и Рис. 1.12, б).
Для схемы замещения с источником ЭДС при 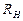 = ∞ (холостой ход) напряжение на зажимах
= ∞ (холостой ход) напряжение на зажимах 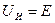 .
.
Дата добавления: 2016-01-18; просмотров: 2462;
