Простейшие геометрические признаки неизменяемости систем.

Как мы уже указывали, аналитический признак по (1.3.1) s=2k является недостаточным для окончательного суждения о неизменяемости системы; поэтому необходимо провести соответствующий анализ ее геометрической структуры. Наиболее целесообразным и общим является геометрический метод исследования неизменяемости основанный на использовании свойств геометрических фигур.

Рисунок 1.3.4.

Первый признак геометрической неизменяемости: ферма неизменяема, если она составлена из шарнирных треугольников (рис.1.3.4) поскольку треугольник неизменяемая геометрическая фигура. В данном случае к исходному треугольнику аbс каждый последующий узел 1, 2, 3, 4 и т. д. прикрепляется двумя стержнями, вследствие чего создается новый треугольник.

Прикрепление узла 1 к узлам b и с двумя стержнями 1_b и Iс, не лежащими на одной прямой, равносильно созданию шарнирно-стержневого неизменяемого треугольника.

Более общий признак геометрической неизменяемости ферм следующий: ферма неизменяема, если каждый последующий узел прикрепляется к двум предыдущим узлам двумя стержнями, осевые линии которых не лежат на одной прямой. Такой структурой обладают все простейшие фермы, представляющие собой совокупность диад (диада —пара наклонных стержней, связанных общим узлом).

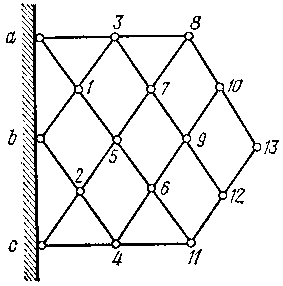
Рисунок 1.3.5.

На рис.1.3.5 изображена консольная ферма с ромбической решеткой, к узлам а, b и с которой двумя стержнями каждый прикрепляются узлы 1, 2, 3, 4, 5, 6 и т.д.

Указанные два признака создания геометрически неизменяемой шарнирно-стержневых систем, однако, неприменимы для анализа геометрической неизменяемости любых ферм