Цепная реакция. Коэффициент размножения. Реактивность.

Ядерные энергетические РЕАКТОРЫ

Цепная реакция. Коэффициент размножения. Реактивность.

Цепная ядерная реакция (ЦР) – это реакция деления ядер урана и плутония нейтронами, рождающимися при делении. Необходимое условие протекания самоподдерживающейся ЦР – рождение в каждом очередном акте деления не менее одного нейтрона. Достаточность этого условия зависит от исхода конкуренции четырех процессов, имеющих место в размножающей среде (среде содержащей нуклиды ядерного топлива):

- Деление ядер топлива;

- Радиационный захват в топливе;

- Радиационный захват нейтронов конструкционными материалами активной зоны и неделящимися компонентами топлива;

- Утечка (вылет) нейтронов за пределы размножающей среды.

ЦР возможна только в том случае, если хотя бы один из родившихся при делении ядра нейтронов снова произведет деление. Количественная характеристика возможности осуществления ЦР – эффективный коэффициент размножения (k_эф), представляющий собой отношение числа нейтронов n₂ в данном поколении к числу нейтронов в поколении предыдущем n₁ (или делений ядер), непосредственно предшествующем поколении:

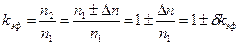. (1.1)

Физический смысл δk_эф – это доля изменения количества нейтронов (делений) в новом поколении по отношению к нейтронам (делениям) предыдущего поколения.

При k_эф>1состояние реактора называют надкритическим (δk_эф>0). При k_эф<1 состояние реактора называют подкритическим (δk_эф<0). Значению δk_эф=0 соответствует критическое состояние реактора (δk_эф=0).

Состоянию реактора с максимально возможной надкритичностью соответствует состояние с максимальным коэффициентом размножения (k_эф^полн), иначе говоря – состояние с всеми полностью извлеченными из активной зоны реактора поглотителями. При этом запас надкритичности составляет: Dk_эф= k_эф^полн -1.

Чаще состояние ядерного реактора (ЯР) характеризуют реактивностью – относительным отклонением k_эф от единицы:

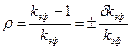, (1.2)

что физически представляет собой долю изменения количества нейтронов (делений) в новом поколении по отношению ко всем нейтронам (делениям) этого поколения.

Следует различать «реактивность» и «запас реактивности». Реактивность r – степень отклонения реактора от критического состояния (т.к. k_эф»1, то r»dk_эф). Запас реактивности r_зап – максимально возможная реактивность при полностью извлеченных из активной зоны реактора поглотителях: r_зап=Dk_эф/ k_эф^полн.

Минимальное количество топлива определенной конфигурации и состава, в котором k_эф=1 (r=0),называют критической массой, а соответствующие размеры размножающей среды – критическими размерами.

Минимальные критические размеры и массу имеет размножающая среда в форме шара. Для ²³⁵U такой шар без отражателя имеет массу ~ 48 кг и радиус ~ 8,5 см. Используя отражатель критическую массу можно уменьшить в 2–3 раза.

При делении ядер U и Pu рождаются нейтроны в широком диапазоне энергий. Распределение нейтронов по скоростям (энергиям) называют спектром нейтронов.

Спектр нейтронов деления – жесткий, в нем преобладают нейтроны высоких энергий (быстрые нейтроны). Максимальное число нейтронов имеет энергию ~ 0,7 МэВ, наибольшая энергия достигает 18 МэВ, средняя – 2 МэВ. В дальнейшем спектр нейтронов изменяется в зависимости от состава размножающей среды.

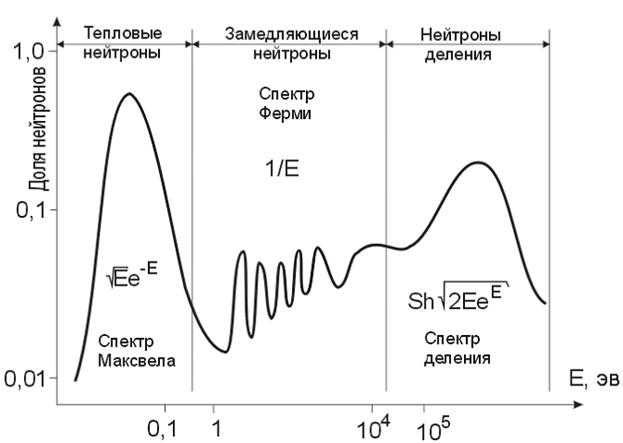
Затем при наличии замедлителя спектр нейтронов смягчается, переходя в спектр Ферми (замедляющиеся нейтроны). При энергиях ~ 1 эв и ниже спектр Ферми переходит в спектр Максвелла (тепловые нейтроны), приближенно описываемый уравнением Максвелла. Процесс установления спектра тепловых нейтронов под влиянием теплового движения атомов среды, а также химических связей атомов и молекул и кристаллических дефектов называют термализацией нейтронов.

Установившийся спектр тепловых нейтронов (спектр Максвелла), находящихся в тепловом равновесии со средой, представляет собой поле свободных нейтронов. Их поведение описывается уравнением газовой кинетики. Температура нейтронного газа (Т_н.г.) совпадает с температурой среды Т. В первом приближении в гомогенной среде

Т_н.г. » Т(1+1,4S_а(Т)/xS_s), [К].

Процесс уменьшения кинетической энергии нейтронов в ходе их движения в среде называют замедлением. Движение нейтронов в среде, когда их энергия в среднем остается постоянной, называется диффузией.

В зависимости от энергии различают нейтроны:

1. сверхбыстрые (Е > 2 МэВ);

2. быстрые (0,2 МэВ < E < 2 МэВ);

3. промежуточные (0,5 кэВ < E < 0,2 МэВ);

4. надтепловые (0,1 эВ < E < 0,5 кэВ);

5. тепловые (Е < 0,1 эВ);

6. холодные (Е < 5×10^-3 эВ).

Замедляясь и диффундируя, нейтроны взаимодействуют с ядрами размножающей среды и перемещаются от места рождения. Односкоростное нестационарное уравнение диффузии имеет следующий вид:

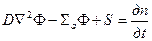
где первый член в левой части характеризует диффузию, второй – поглощение и третий – генерацию нейтронов. Правая часть представляет собой изменение плотности во времени. D – коэффициент диффузии нейтронов, см; Σ_а – макроскопическое сечение поглощения, см^-1; S – плотность источников нейтронов, нетр/(см³×с).

Возраст нейтрона t (м²) – мера среднего расстояния по прямой t_зам, на которое смещается нейтрон от точки рождения с энергией Е₀ до точки, где он замедлился до энергии Е.

Для среды с точечным источником:

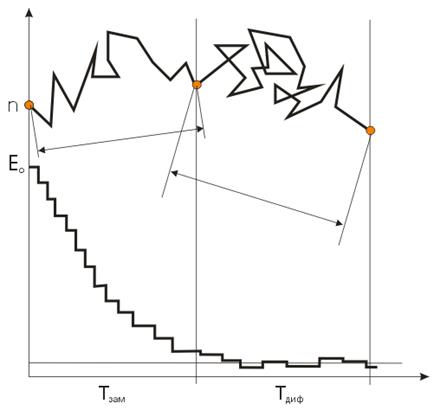
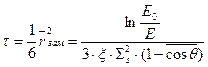. (1.3)

Средний логарифмический декремент энергии нейтрона x характеризует потерю энергии нейтром (при столкновении с ядром), имевшим до столкновения энергию Е₁, а после столкновения энергию Е₂:

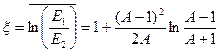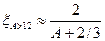; . (1.4)

Среднее число столкновений, необходимых для замедления нейтрона деления с энергией Е₁ до энергии Е₂ в замедлителе с логарифмическим декрементом x,

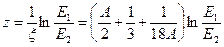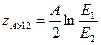; (1.5)

Для замедления от средней энергии нейтрона 2 МэВ до тепловой энергии 0,025 МэВ количество столкновений z = 18,2/x.

Длина диффузии нейтрона L (м) – мера среднего расстояния по прямой, (r_диф), на которое смещается нейтрон от точки, где он стал тепловым, до точки поглощения. Для среды с точечным источником:

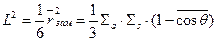. (1.6)

Длина миграции нейтрона М (м²) – мера среднего расстояния по прямой, на которое смещается нейтрон от точки рождения до точки поглощения:

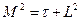(1.7)

Коэффициент замедления нейтронов характеризует способность вещества замедлять нейтроны и сохранять их (не поглощать) – К_зам=xS_s/S_a, где xS_s – замедляющая способность замедлителя, м^-1.

С использованием введенных выше характеристик пространственного поведения нейтронов в размножающей среде k_эф для критического ЯР на тепловых нейтронах записывается так:

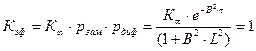(1.8)

k_эф определяется энергией нейтронов, осуществляющих ядер топлива, составом и свойством компонентов, размерами и формой размножающей среды.

р_зам=exp(-B²×t) – вероятность нейтрону избежать утечки в процессе замедления.

Р_диф=(1+В²×L²)^-1 – вероятность нейтрону избежать утечки в процессе диффузии.

В – геометрический параметр, который в активной зоне радиусом R (м) и высотой Н (м) определяется из соотношения:

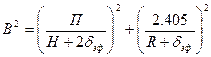[м^-2] (1.9)

d_эф – эффективная добавка – уменьшение линейных размеров активной зоны за счет отражателя нейтронов. Коэффициент размножения нейтронов ЯР на тепловых нейтронах для бесконечной среды, т.е. без учета утечки нейтронов:

К_¥=n_эф×m×j×q (1.10)

n_эф – эффективный выход нейтронов на один захваченный нейтрон в топливе.

m – коэффициент размножения на быстрых нейтронах.

j – вероятность избежать резонансного захвата нейтрона ²³⁸U.

q – коэффициент использования тепловых нейтронов.

Количественными характеристиками распределения нейтронов в размножающей среде являются следующие величины:

- Плотность нейтронов n (нейтр./см³) – отношение числа нейтронов dn¢ (нейтр.) в элементарной сфере объемом dV (см³) к этому объему: n= dn¢ /dV.

- Поток нейтронов I_n – отношение числа нейтронов dn¢ (нейтр.), падающих на данную поверхность за интервал времени dt ®, к этому интервалу: I_n= dn¢ / dt.

- Плотность потока нейтронов Ф (нейтр./см²×с) – отношение потока нейтронов dI_n (нейтр./с) проникающих в объем элементарной сферы, к площади поперечного сечения этой сферы dS (см²): Ф= dI_n/ dS.

- Флюенс нейтронов F (нейтр./см²) – отношение числа нейтронов dn¢ (нейтр.), проникающих в объем элементарной сферы, к площади поперечного сечения этой сферы dS (см²), т.е. суммарное число нейтронов, прошедших через единицы площади поверхности за время t (с): F= dn¢ / dS=Фt.

Физически Ф можно представить как полный путь который проходят все нейтроны со скоростью v (см/с) в единице объема за единицу времени: Ф=v×n.