Квантовая теория электропроводности металлов
В отсутствие внешнего электрического поля электронный газ в металлах находится в равновесном состоянии и описывается равновесными функциями распределения.
Для вырожденного газа такой функцией является функция Ферми-Дирака, а для невырожденного – функция Максвелла-Больцмана.
 При равновесии электрического тока нет. Однако электроны в твердом теле движутся в периодическом потенциальном поле ионов. Их поведение описывается с помощью волновых функций, являющихся решением уравнения Шредингера. При этом энергия электронов квантуется, т. е. принимает дискретные значения.
При равновесии электрического тока нет. Однако электроны в твердом теле движутся в периодическом потенциальном поле ионов. Их поведение описывается с помощью волновых функций, являющихся решением уравнения Шредингера. При этом энергия электронов квантуется, т. е. принимает дискретные значения.
Т. е. приходится следить не за поведением конкретного электрона, а за квантовым состоянием.
Тогда не важно, какой электрон, не важно, какая частица несет заряд и массу электрона…
Это «как бы» свободная частица – «квазичастица».
Рассматривая движение таких свободных квантовых частиц в периодическом поле кристалла, приходится наделять электроны особой массой – эффективной массой m*.
Эффективная масса m*, заключая в себе всю особенность, присущую электрону, движущемуся в периодическом поле кристалла, является весьма своеобразной величиной.
Прежде всего она может быть как положительной, так и отрицательной величиной, а по абсолютному значению может быть как намного больше массы электрона, так и намного меньше.
Электроны, расположенные у дна энергетической зоны, имеют положительную m*, поэтому во внешнем электрическом поле они ведут себя «нормально» - ускоряются в направлении действия электрической силы.
Для электронов, находящихся у вершины энергетической зоны, m* < 0 (отрицательная), поэтому они ведут себя аномально - ускоряются по направлению поля.
Эффективная масса не определяет ни инертные, ни гравитационные свойства электрона. Она лишь характеризует его взаимодействие с электрическим полем кристалла.
Заменяя массу электрона на m*, можно рассматривать электроны проводимости в металле как идеальный газ, но газ с совершенно необычными квантовыми свойствами. При этом электроны движутся в вязкой среде кристалла, которая препятствует их направленному движению, обладая некоторым сопротивлением.
Тогда можно получить оценку скорости дрейфа электронов в металле при наличии электрического поля
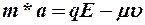 ,
,
где 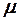 - коэффициент сопротивления кристалла движению электрона.
- коэффициент сопротивления кристалла движению электрона.
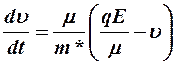 ,
,
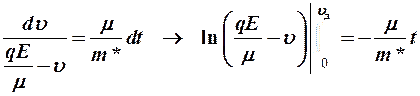
откуда 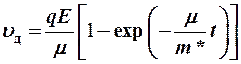 .
.
При 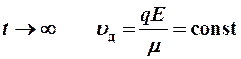 .
.
Так как 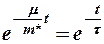 , где
, где 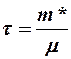 - время релаксации, т. е. время, за которое дрейфовая скорость изменяется в «е» раз.
- время релаксации, т. е. время, за которое дрейфовая скорость изменяется в «е» раз.
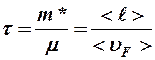 ,
,
где 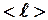 - средняя длина свободного пробега электронов, которому в металле мешают двигаться фононы (квазичастицы тепловых волн в кристаллах).
- средняя длина свободного пробега электронов, которому в металле мешают двигаться фононы (квазичастицы тепловых волн в кристаллах).
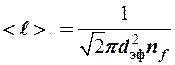 ,
,
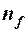 - концентрация фононов в кристалле,
- концентрация фононов в кристалле,
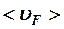 - средняя скорость электронов в кристаллах
- средняя скорость электронов в кристаллах
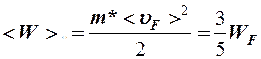 .
.
Тогда 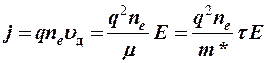 ,
,
откуда 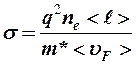 . (13-3)
. (13-3)
Полученный результат практически совпадает с классическим (13-2), но величины, входящие в (13-3) и (13-2), имеют принципиальную разницу.
Классическая физика считала, что электроны при своем движении сталкиваются с узлами кристаллической решетки, проходя при этом в среднем расстояние 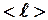 , равное межузельному расстоянию, которое постоянно и
, равное межузельному расстоянию, которое постоянно и 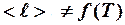 , а вот средняя скорость теплового (хаотического) движения
, а вот средняя скорость теплового (хаотического) движения 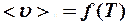 , причем
, причем 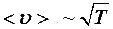 .
.
Квантовая физика считает, что электроны при своем движении рассеиваются на тепловых флуктуациях кристаллической решетки (фононах), концентрация которых 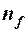 сильно зависит от температуры, при этом средняя скорость теплового движения
сильно зависит от температуры, при этом средняя скорость теплового движения 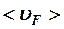 практически не зависит от температуры, т. к. тепловому возбуждения подвергается небольшое количество электронов, находящихся вблизи уровня Ферми
практически не зависит от температуры, т. к. тепловому возбуждения подвергается небольшое количество электронов, находящихся вблизи уровня Ферми
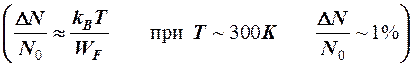 .
.
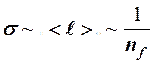 ;
; 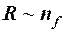 .
.
В области высоких температур 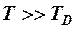 все осцилляторы возбуждены вплоть до
все осцилляторы возбуждены вплоть до 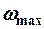 , тогда с ростом температуры
, тогда с ростом температуры 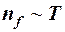 и
и
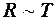 ,
,
что очень хорошо согласуется с экспериментом.
В области низких температур 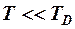 с ростом температуры происходит не только увеличение фононов с данной частотой, но и быстрый рост новых фононов.
с ростом температуры происходит не только увеличение фононов с данной частотой, но и быстрый рост новых фононов.
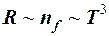 (
( 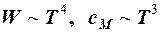 ),
),
что также хорошо согласуется с экспериментом.
 |
В области сверхнизких температур вблизи 0 К концентрация фононов становится столь малой, что основную роль в рассеянии электронов начинают выполнять примеси, концентрация которых не зависит от температуры, и тогда
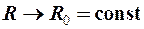 .
.
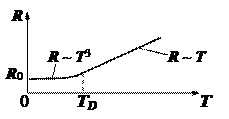
Дата добавления: 2016-01-18; просмотров: 2232;
