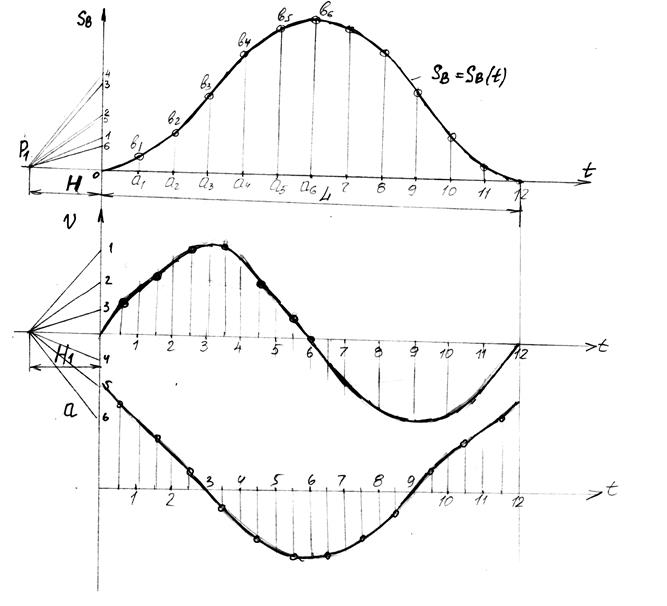
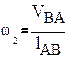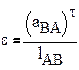Построение диаграммы перемещения.
Строим 12 положений (см.рис.1)
За начало отсчета принимаем положение поршня Во.
Затем выбрав систему координат sb ,t по оси абсцисс откладываем отрезок L(мм) соответствующий времени Т одного оборота кривошипа.
Откладываем Y1= kBoB1; Y2=kВоВ2 и т.д., где BoB1; BoB2 и т.д. отрезки, отражающие перемещения т.В на планах механизма.
 k-коэффициент кратности ординат графика Sв=Sв(t) и
k-коэффициент кратности ординат графика Sв=Sв(t) и
Рис.2
отрезков изображающих перемещения BoB1, BoB2 т.В на планах механизма.
Между масштабом плана механизма и масштабом ординат диаграммы перемещений существует зависимость:
 μs= μs=
| 1k | *μe |
Масштаб времени, откладываемого по оси абсцисс:
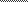 μt= μt=
| T L | (сек./мин.) |
где Т - время одного оборота ведущего звена в секундах. Если число оборотов кривошипа =n (об/мин), то
  T= T=
| n | (сек) при этом | μt= | nT | (сек./мин.) |
Аналогично строится график угловых перемещений звена совершающее вращательное движение. В этом случае по оси ординат откладываются отрезки пропорциональные величинам угловых перемещений.
Построение графиков скорости и ускорения по графику перемещения.
 Построение графиков V=V(t) и a=a(t) по графику S=S(t) осуществляется методом графического дифференцирования, сущность которого заключается в следующем.
Построение графиков V=V(t) и a=a(t) по графику S=S(t) осуществляется методом графического дифференцирования, сущность которого заключается в следующем.
Пусть есть перемещение некоторой точки за малый промежуток времени. Проведем секущую ВС, а из полюса Р, выбранного произвольно на расстоянии Н от начала координат луч, параллельный ВС. Из подобия РАО и ВОД следует:
      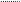 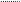  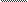 OA
H OA
H
| = | CD BD | OA= | CD BD | *H | (1) |
Действительное значение перемещения за время отображается отрезком:
 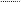 CD= CD=
| ∆S μs |
 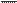 отрезок оси абсцисс отрезок оси абсцисс
| а1 а2 = | BD= | ∆t μt | -отображает длительность интервала времени в масштабе. |

Подставив эти значения CD и BD в равенство (1) найдем:
   OA= OA=
| ∆S ∆t | * | μt μs | *H | (2) |
отношение представляет среднее значение скорости движения точки на пути длинной ∆S, то следует:
 Vср= Vср=
| ОА* | μs μt* H | (3) |
 Если принять масштаб скорости Если принять масштаб скорости
| μV= | μs μt* H | то из равенства (3) отрезок ОА |
отображает величину средней скорости движения точки.
Допуская некоторую погрешность, считают, что это среднее значение скорости соответствует среднему мгновению промежутка t, т.е. точке F.
При изложенном способе дуга ВС заменилась хордой ВС. Допустима также замена дуги соответствующим отрезком касательной. В обоих случаях результаты получаются с погрешностью.
(Рассмотрим на примере рис.2)
График ускорения строится аналогично, путем дифференцирования графика V. При этом новое полюсное расстояние H1≠H
 Определение масштаба графика a получаем, заменив величину μs→μV а вместо H→H1
Определение масштаба графика a получаем, заменив величину μs→μV а вместо H→H1
 μa= μa=
| μV μt*H1 |
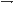 Вследствии двукратного дифференцирования, диаграммы a могут получиться со значительными искажениями.
Вследствии двукратного дифференцирования, диаграммы a могут получиться со значительными искажениями.

 Поэтому рассмотрим другой способ определения скоростей и ускорений.
Поэтому рассмотрим другой способ определения скоростей и ускорений.
Метод планов скоростей и ускорении базируется на теоремах о скольжении векторов скоростей и ускорений, доказываемых в курсах теоретической механики.
 | |||
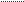 |
Теорема 1 Вектор скорости абсолютного движения точки (Va) равен сумме

 векторов скоростей переносного (Ve) и относительного (Vr) движений.
векторов скоростей переносного (Ve) и относительного (Vr) движений.
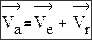 эта теорема была известна еще Архимеду (287-212 гг.д.н.э.)
эта теорема была известна еще Архимеду (287-212 гг.д.н.э.)
Теорема 2 (Кориолиса) Вектор ускорения (аn) абсолютного движения материальной точки равен сумме векторов ускорений переносного (ае) и
относительного движений (аr) и ускорения Кориолиса (ac):
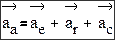
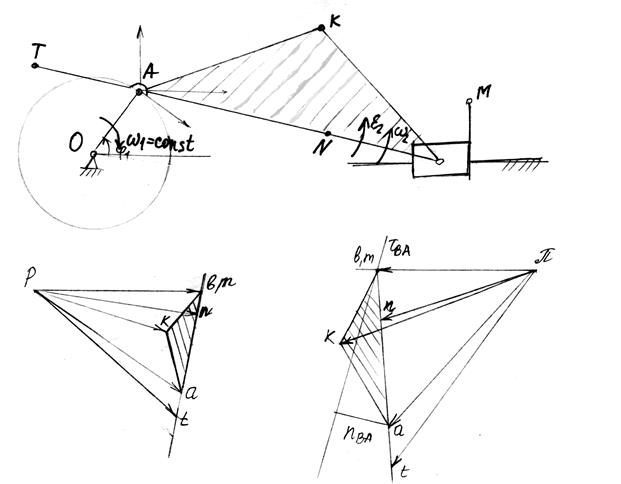
Метод планов скоростей и ускорений. 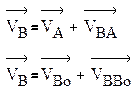
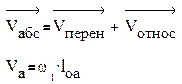
VВА^ВА 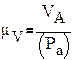
VВо=0 VВвоô ô x-x
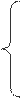 Все точки координатной системы движутся с одинаковой скоростью. После того, как найдены скорости шарнирных точек механизма, скорости других точек определяем с помощью теоремы подобия:
Все точки координатной системы движутся с одинаковой скоростью. После того, как найдены скорости шарнирных точек механизма, скорости других точек определяем с помощью теоремы подобия:
все жесткие фигуры на плане механизма подобны одноименным фигурам на плане скоростей, а их сходственные стороны взаимно перпендикулярны.
Δ АКВ ~ Δ акв
Планы ускооений

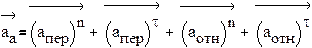 -теорема о сложении ускорений, когда переносное ускорение по форме поступательное.
-теорема о сложении ускорений, когда переносное ускорение по форме поступательное.
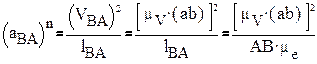 |
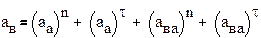
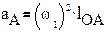 |
о
аВô ô x-x
Для определения ускорения остальных точек используем теорему подобия: все неизменяемые фигуры на плане механизма подобны одноименным фигурам на плане усковений.
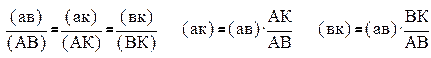
Методом засечек получим две точки, одна из них ложная, чтобы найти истинную точку, применяют правило обхода вершин:
порядок чтения вершин при обходе подобных контуров в какую-либо, но одну и ту же сторону, не должен изменяться.
Определение угловых скоростей и угловых ускорений звеньев механизмов
|
|
Шатун АВ вращается ускоренно, т.к. ω2 и ε2 направлены в одну сторону. Если ω и ε направлены в разные стороны, то ползун движется замедленно.
Механизмы с высшей кинематической парой.
В этом разделе будут рассмотрены передаточные механизмы с высшей КП, а именно:
1. цилиндрические зубчатые передачи с эвольвентным профилем зубов и постоянным передаточным отношением;
2. планетарные механизмы с подвижными осями зубчатых колес.
Достоинство механизмов с высшей КП:
1. малые габариты и вес;
2. возможность точного воспроизведения закона движения выходного звена (по сравнению с рычажными механизмами зубчатые передачи имеют меньше зазоров);
3. высокий КПД (0,85 – зубчатая передача, 0,99 – планетарный механизм).
Недостатки:
наличие высшей КП может привести к повышенным удельным давлениям в точке контакта. Это в свою очередь может привести к выкрашиванию материалов (питтинг).
Дата добавления: 2016-01-18; просмотров: 963;