Способ цепных подстановок
Способ цепных подстановок позволяет измерить влияние отдельных факторов на результат их взаимодействия - обобщающий (целевой) показатель, рассчитать отклонения фактических показателей от нормативных (плановых).
Это один из элементов методики экономического анализа, который заключается в последовательной замене плановой величины одного из алгебраических слагаемых, одного из сомножителей фактической его величиной при сохранении неизменными остальных показателей.
Метод цепных подстановок используется для исчисления влияния отдельных факторов на соответствующий совокупный показатель. Данный способ анализа используется, когда зависимость между изучаемыми явлениями имеет строго функциональный характер, когда она представляется в виде прямой или обратно пропорциональной зависимости. В этих случаях анализируемый совокупный показатель как функция нескольких переменных должен быть изображен в виде алгебраической суммы, произведения или частного от деления одних показателей на другие.
Степень влияния того или иного показателя выявляется последовательным вычитанием: из второго расчета вычитается первый, из третьего - второй и т.д. В первом расчете все величины плановые, в последнем - фактические. Отсюда следует правило, заключающееся в том, что число расчетов на единицу больше, чем число показателей расчетной формулы. При определении влияния двух факторов (показателей) делают три расчета, трех факторов - четыре расчета, четырех факторов - пять расчетов. Но поскольку первый расчет включает лишь плановые величины, то его результаты можно взять в готовом виде из плана предприятия или объединения; результат последнего расчета, когда все показатели фактические, - из квартального или годового отчета. Следовательно, практически число расчетов оказывается не на единицу больше, а на единицу меньше, т.е. осуществляются лишь промежуточные расчеты.
Алгоритм метода цепных подстановок можно продемонстрировать на примере расчёта влияния изменений величин частных показателей на величину показателя, представленного в виде следующей расчетной формулы: F = a·b·c, т.е. в виде мультипликативной модели.
Здесь и далее 0 соответствует базисному периоду (это – индекс базисного показателя);
1 соответствует отчётному периоду (это – индекс показателя в отчётном периоде).
Тогда базисное значение F будет равно F0 = a0·b0·c0, а фактическое: F1 = a1·b1·c1.
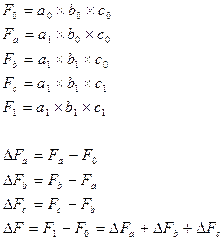 Общее отклонение фактического показателя от базисного F (F=F1–F0) , очевидно, равно сумме отклонений, полученных под влиянием изменения частных показателей:
Общее отклонение фактического показателя от базисного F (F=F1–F0) , очевидно, равно сумме отклонений, полученных под влиянием изменения частных показателей:
F = Fa+Fb+Fc.
А изменения частных показателей вычисляются путём последовательных подстановок в формулу для вычисления показателя F фактических значений параметров a, b, c, вместо базисных:
Проверка расчета проводится путем сопоставления баланса отклонений, т.е. общее отклонение фактического показателя от базисного должно быть равно сумме отклонений под влиянием изменения частных показателей: F1–F0 = Fa+Fb+Fc..
ПРИМЕР ЦЕПНЫХ ПОДСТАНОВОК
Вычисление с использованием метода цепных подстановок проиллюстрируем на конкретном примере. Допустим, требуется определить влияние на объем промышленной продукции трудовых факторов. Объем промышленного производства может приниматься в виде валовой, товарной, реализованной или чистой продукции. Зависимость объема продукции от трудовых показателей математически выражается так (т.е.. тоже мультипликативная модель):
Q = RTдТчWч (1)
где Q - объем выпуска продукции;
R - среднесписочное число рабочих;
Tд - среднее число дней, отработанных одним рабочим за год;
Тч - среднее число часов, отработанных одним рабочим за день;
Wч - средняя выработка продукции на один отработанный человеко-час.
Следовательно, объем продукции равен произведению четырех показателей. Для оценки влияния каждого из них необходимо сделать пять расчетов, исходные данные для которых приведены в табл. 1.
Стоимость фактического объема продукции больше плановой на 3155,2 - 2803,8 - 351 ,4 тыс. руб.
Таблица 1
Значение трудовых факторов
| Показатели | Обознач. | Плановые | Фактические |
| Объем продукции (тыс. руб.) | F | 2803,8 | 3155,2 |
| Среднесписочное число рабочих {чел.} | a | ||
| Среднее число дней, отработанных одним рабочим в год | b | ||
| Среднее число часов, отработанных одним рабочим в день | c | 6,9 | 6,8 |
| Ср. выработка продукции на одни отработанный человеко-час (тыс. руб.) | d | 1,50 | 1,60 |
Рассчитаем, как повлияли на объем продукции различные факторы.
1) Все показатели плановые:
F0=900 • 301 • 6,9 • 1,50 = 2803,8 (тыс. руб.).
2) Среднесписочное число рабочих фактическое; остальные показатели плановые:
Fa=1000 • 301 • 6,9• 1,50 = 3115,4 (тыс. руб.).
3) Число рабочих и число отработанных ими дней фактические; остальные показатели плановые:
Fab=1000 • 290 • 6,9 • 1,5 = 3001,5 (тыс. руб.).
4) Число рабочих, число отработанных дней и часов фактические; выработка плановая:
Fabc=1000 • 290 • 6,8 • 1,50 = 2958,0 (тыс. руб.).
5) Все показатели фактические:
Fabcd=F1=1000 • 290 • 6,8 • 1,60 = 3155,2 (тыс. руб.).
План производства продукции перевыполнен на 351,4 (ΔF=F1-F0=3155,2-2803,3).
Отклонение фактического объема продукции от планового произошло за счет влияния следующих факторов:
увеличения числа рабочих ΔFa=Fa-F0=3115,4 - 2803,8 = +311,6
уменьшения числа отработанных дней ΔFb=Fab-Fa=3001,5 - 3115,4 = - 113,9
уменьшения средней продолжительности ΔFc=Fabc-Fab=2958,0 - 3001,5 = - 43,5
рабочего дня
повышения средней часовой выработки ΔFd=Fabcd-Fabc=3155,2 - 2958.0 = + 197.2
Общее отклонение 3155,2 - 2803,8 = + 351,4 (тыс. руб.)
Следовательно, увеличение числа рабочих и повышение среднечасовой выработки повлияли на выпуск продукции положительно, а уменьшение числа отработанных дней и средней продолжительности рабочего дня - отрицательно.
Расчет показывает, что на предприятии были целодневные и внутрисменные простои, превышавшие плановые показатели. Если бы предприятие не допустило рост неявок и внутрисменных простоев (сверх допустимого), то было бы выработано продукции больше на 157,4 (113,9+43,5).
Недостаток метода состоит в том, что, в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения. Это связано с тем, что в результате применения этого метода образуется некий неразложимый остаток, который прибавляется к величине влияния последнего фактора. На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора.
Однако существуют определенные правила, определяющие последовательность подстановки:
- при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается изменение количественных факторов;
- если модель представлена несколькими количественными и качественными показателями, то в первую очередь определяется влияние факторов первого порядка, затем второго и т.д.
В зависимости от содержания показателей и алгоритма их расчета выделяются факторы первого порядка, которые непосредственно определяют размеры результативного показателя (увеличение численности рабочих, объемов продукции и т.д.). Факторы второго порядка воздействуют на результат через факторы первого уровня и т.д.
Под количественным факторами при анализе понимают те, которые выражают количественную определенность явлений и могут быть получены путем непосредственного учета (количество рабочих, станков, сырья и т.д.).
Качественные факторы определяют внутренние качества, признаки и особенности изучаемых явлений (производительность труда, качество продукции, ср. продолжительность рабочего дня и т.д.).
Например, если требуется определить степень влияния численности работников и производительности труда на размер выпуска промышленной продукции, то прежде устанавливают влияние количественного показателя - численности работников, а потом качественного - производительности труда. Если выясняют влияние факторов количества и цен на объем реализованной промышленной продукции, то вначале исчисляют влияние количества, а потом - влияние оптовых цен.
Прежде чем приступить к расчетам, необходимо,
во-первых, выявить четкую взаимосвязь между изучаемыми показателями (факторную модель),
во-вторых, разграничить количественные и качественные показатели,
в-третьих, правильно определить последовательность подстановки в тех случаях, когда имеется несколько количественных и качественных показателей (основных и производственных, первичных и вторичных).
Произвольное изменение последовательности подстановки меняет количественную весомость того или иного показателя. Чем значительнее отклонение фактических показателей от плановых, тем больше и различий в оценке факторов, исчисленных при разной последовательности подстановки.
Покажем это на простейшем примере. Допустим, что затраты сырья на производство какого-либо изделия составляют:
| Показатели | Плановые | Фактические | Отклонение |
| Количество сырья, кг | - 5 | ||
| Себестоимость 1 кг сырья, руб. | 5,00 | 4,50 | - 0,50 |
| Сумма, руб. | 112,5 | - 37,5 |
На сумму израсходованных материалов влияли два фактора: фактор норм и фактор цен. В соответствии с упрощенными правилами цепной подстановки здесь должен быть лишь один промежуточный расчет, так как плановые и отчетные показатели содержатся в условии.
Промежуточный расчет произведем с различной последовательностью:
а) в первую очередь подставляется фактическое значение количества
25 • 5 = 125;
б) во вторую очередь подставляется фактическое значение себестоимости
4,5 • 30 = 135.
Находим влияние указанных факторов:
а) при первой последовательности подстановки:
фактор норм 125 - 150 = - 25;
фактор цен 112,5 - 125 = - 12,5;
б) при второй последовательности подстановки:
фактор норм 112,5 - 135 = - 22,5;
фактор цен 135 - 150 = - 15.
И в первом, и во втором случаях мы получим одно и то же общее отклонение (-37,5), но весомость первого и второго факторов существенно изменилась.
Метод цепной подстановки имеет недостаток, сущность которого состоит в возникновении неразложимого остатка, который присоединяется к числовому значению влияния последнего фактора, в данном случае к фактору цен. Именно этим и объясняется разница в расчетах при изменении последовательности подстановки.
Этот недостаток устраняется с помощью математических методов анализа.
Дата добавления: 2016-01-18; просмотров: 2307;
