Собственные полупроводники и их проводимость

Собственные полупроводники – это твердые вещества, состоящие из элементов IV группы таблицы Менделеева (германий Ge, кремний Si).

Т. к. их валентность равна 4, то на валентном уровне каждого атома находятся по 4 валентных электрона.

При образовании из отдельных атомов твердого тела (когда атомы приближаются друг к другу так близко, что происходит перекрытие электронных облаков) валентные электроны обобществляются и образуют прочные атомные (обменные, а в химии – ковалентные) связи.

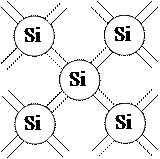Пространственная схема образования ковалентных связей в собственных полупроводниках.

Свободных электронов нет – это непроводящее вещество (диэлектрик).

По зонной теории в собственных полупроводниках все уровни валентной зоны заняты электронами, а до ближайшей свободной зоны (зоны проводимости) лежит неширокая запрещенная зона (с 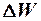d 1 эВ).

Поведение электронов в твердом теле описывается функцией распределения Ферми-Дирака, которая позволяет вычислить вероятность заполнения электронами того или иного квантового состояния:

.

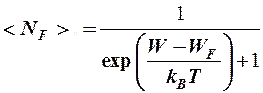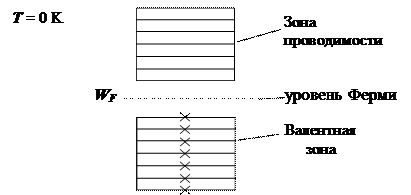
При Т = 0 К электроны занимают все уровни, начиная с самых нижних, вплоть до уровня Ферми (это энергетический уровень электрона в твердом теле, вероятность заполнения которого при любой температуре равна 1/2).

Т. к. при Т = 0 К все уровни валентной зоны заняты электронами ( < N_F > = 1), а уровни зоны проводимости свободны ( ), тогда уровень Ферми (где ½) должен находиться ровно посередине запрещенной зоны. Но т. к. значения энергии запрещенной зоны не могут быть реализованы электронами твердого тела, тогда уровень Ферми для полупроводников вводится условно – посредине запрещенной зоны (но он в полупроводниках никогда не бывает занят электроном).

При наложении на такое вещество слабого электрического поля электроны не могут разорвать прочные ковалентные связи (а по зонной теории – не могут преодолеть запрещенную зону) и стать свободными.

Но если собственному полупроводнику сообщить дополнительную энергию (~ 1 эВ), достаточную для разрушения ковалентных связей (достаточную для преодоления электроном запрещенной зоны), то электрон становится свободным (оказывается в зоне проводимости).

Для электронов, появившихся на нижних уровнях зоны проводимости, функция распределения Ферми-Дирака будет иметь значение:

.

Даже для комнатных температур (Т ~ 300 К) 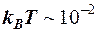эВ, тогда т. к. 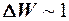эВ 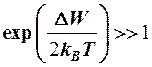, значит

,

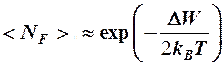а это есть функция распределения Максвелла-Больцмана (вырождение снимается, т. к. число электронов N в зоне проводимости << числа возможных квантовых состояний G в этой зоне (N<<G)).

Концентрация свободных электронов в полупроводниках

.

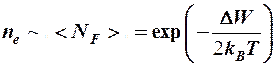На месте разорванной ковалентной связи остается нескомпенсированный положительный заряд (перешедший в зону проводимости электрон освобождает энергетический уровень в валентной зоне). Это освободившееся место (освободившийся уровень) может быть занято другим электроном.

Тогда создается ситуация, когда положительный заряд начинает как бы перемещаться по кристаллу подобно частице – это «квазичастица», которую назвали «дыркой».

Т. о. при разрыве ковалентных связей образуются свободные электроны и дырки, возникает электронно-дырочная (собственная) проводимость.

Удельная проводимость собственного полупроводника

,

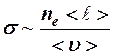где 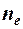- концентрация свободных носителей заряда (электронов, дырок);

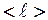- средняя длина свободного пробега электронов (рассеяние происходит на фононах в полупроводниках), ,

при ,

при ;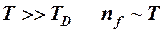

- средняя скорость теплового (хаотического) движения электронов (для классических частиц ).

Степенная зависимость пр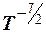и или гораздо слабее экспоненциальной, значит можно записать для удаленной проводимости собственного полупроводника

.

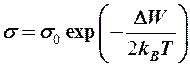Т. к. , тогда можно записать

.

,

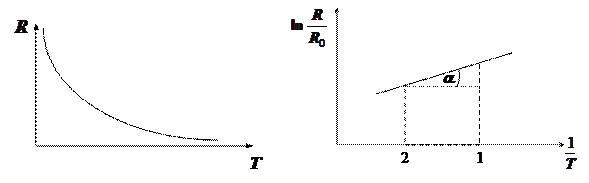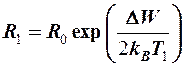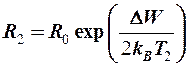
Т. е. по tg угла наклона кривой 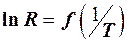можно определить энергию активации (ширину запрещенной зоны) полупроводника.

С ростом температуры сопротивление собственного полупроводника быстро уменьшается несмотря на тот факт, что с ростом температуры увеличивается и количество фононов, которые мешают двигаться электронам ( 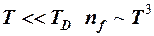, ). Но этот процесс менее интенсивный по сравнению с лавинообразным нарастанием количества свободных электронов и дырок. Это в итоге приводит к практически экспоненциальному снижению сопротивления полупроводника при увеличении температуры.

Сильная зависимость сопротивления собственных полупроводников от температуры используется в терморезисторах (датчики пожарной сигнализации).