Вершин теодолитного хода
| Номера точек | Измерен- ные углы bi | Исправлен- ные углы bиспр | Дирекцион- ные углы ai | Румбы ri | ||
| ° ' '' | ° ' '' | ° ' '' | назв. | ° ' '' | ||
| п/п85 | - | - | ||||
| 50 21 34 | СВ | 50 21 34 | ||||
| п/п84 | 202 48 00 | 202 48 20 | ||||
| 27 33 14 | СВ | 27 33 14 | ||||
| 199 12 30 | 199 12 51 | |||||
| 8 20 23 | СВ | 8 20 23 | ||||
| 70 10 00 | 70 10 20 | |||||
| 118 10 03 | ЮВ | 61 49 57 | ||||
| 106 46 30 | 106 46 51 | |||||
| 191 23 12 | ЮЗ | 11 23 12 | ||||
| п/п83 | 194 39 00 | 194 39 20 | ||||
| 176 43 52 | ЮВ | 03 16 08 | ||||
| п/п82 | ||||||
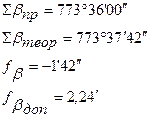
| ||||||
Окончание табл. 1.4
| Горизон-тальное проло- жение | Приращения координат, м | Координаты, м | |||||||||
| вычисленные | исправленные | ||||||||||
| d, м | + - | Δx | + - | Δy | + - | Δx | + - | Δy | x | y | |
| 607,50 | 1062,50 | ||||||||||
| 68,74 | + | -0,02 60,94 | + | +0,01 31,80 | + | 60,92 | + | 31,81 | |||
| 668,42 | 1094,31 | ||||||||||
| 190,36 | + | -0,06 188,35 | + | +0,03 27,61 | + | 188,29 | + | 27,64 | |||
| 856,71 | 1121,95 | ||||||||||
| 104,18 | - | -0,03 49,18 | + | +0,01 91,84 | - | 49,21 | + | 91,85 | |||
| 807,50 | 1213,80 | ||||||||||
| 110,05 | - | -0,03 107,88 | - | +0,02 21,73 | - | 107,91 | - | 21,71 | |||
| 699,59 | 1192,09 | ||||||||||
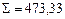 м м
| 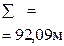
|
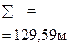
| 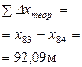
| 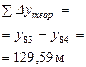
| |||||||
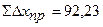 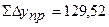 м м
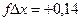 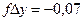 м м
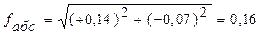 м м
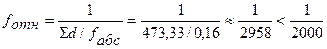 м м
|
Для рассматриваемого примера 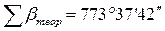 .
.
В нашем примере 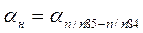 ;
; 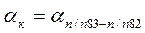 .
.
Вследствие ошибок измерений углов практическая сумма измеренных горизонтальных углов не равна теоретической сумме горизонтальных углов, разность между ними называют угловой невязкой.
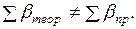
3. Вычисляется угловая невязка хода. Разница между 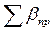 и
и 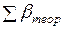 и составляет угловую невязку в разомкнутом теодолитном ходе.
и составляет угловую невязку в разомкнутом теодолитном ходе.
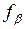 =
= 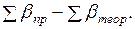 (1.13)
(1.13)
Полученную невязку сравнивают с допустимой, которая вычисляется по формуле
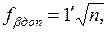 (1.14)
(1.14)
где n – число измеренных углов.
В нашем примере 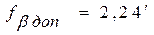 . Если выполняется неравенство
. Если выполняется неравенство 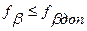 , то
, то 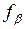 делят на количество углов и получают величину поправки, которую вводят в каждый измеренный горизонтальный угол с обратным знаком:
делят на количество углов и получают величину поправки, которую вводят в каждый измеренный горизонтальный угол с обратным знаком:
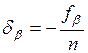 . (1.15)
. (1.15)
Поправки вычисляются до целых секунд. Должно выполняться равенство 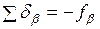 . К измеренным углам прибавляют поправку со своим знаком, результат записывают в графу 3.
. К измеренным углам прибавляют поправку со своим знаком, результат записывают в графу 3. 
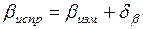 . (1.16)
. (1.16)
Контролем правильности исправления углов служит равенство
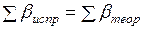 . (1.17)
. (1.17)
После уравнивания углов вычисляют дирекционные углы всех сторон хода по формуле
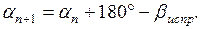 (1.18)
(1.18)
Дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180º и минус правый (исправленный) угол хода, образованный этими сторонами.
Пример.
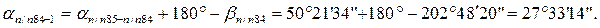 Для нашего хода вычисления ведут в следующей последовательности:
Для нашего хода вычисления ведут в следующей последовательности:
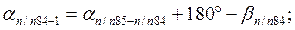
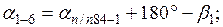
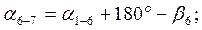
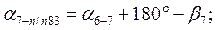
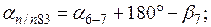

Вычисленный 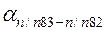 должен быть точно равен исходному
должен быть точно равен исходному 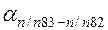 . Результаты вычислений записывают в графу «Дирекционные углы».
. Результаты вычислений записывают в графу «Дирекционные углы».
Если при вычислении дирекционный угол получается отрицательным, то кроме 180º к дирекционному углу предыдущей стороны необходимо прибавить 360º. Если дирекционный угол получается больше 360º, то из него вычитают 360º.
4. Производят уравнивание линейных измерений. Обработка линейных измерений начинается с вычисления приращений координат для всех сторон теодолитного хода по формулам
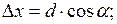
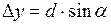 , (1.19)
, (1.19)
где d – горизонтальное проложение стороны хода; 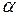 – дирекционный угол этой же стороны.
– дирекционный угол этой же стороны.
 Вычисленные приращения координат (
Вычисленные приращения координат ( 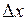 и
и 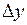 ) записывают в графы 9 и 11 табл. 1.4, находят их суммы
) записывают в графы 9 и 11 табл. 1.4, находят их суммы 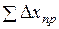 ,
, 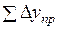 и приступают к их уравниванию.
и приступают к их уравниванию.
Зная координаты начальной точки 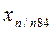 и
и 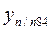 и приращения, можно вычислить координаты всех точек теодолитного хода:
и приращения, можно вычислить координаты всех точек теодолитного хода:
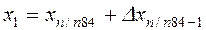 ;
; 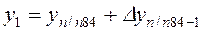 ;
;
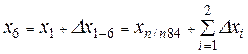 ;
; 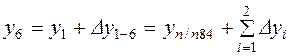 ;
;
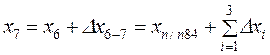 ;
; 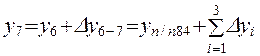 ;
;
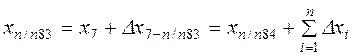 ;
; 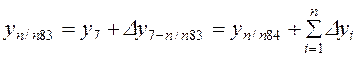 ,
,
где п – число измеренных сторон хода.
Из последней строки системы определим 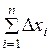 и
и 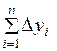 :
:
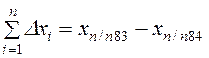 ;
; 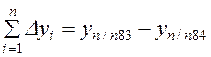 . (1.20)
. (1.20)
Или в общем виде 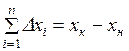 ;
; 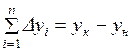 .
.
Эти формулы справедливы тогда, когда приращения координат не имеют погрешностей. Поэтому суммы данных приращений называют теоретическими и обозначают через 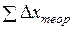 и
и 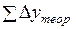 , т.е.
, т.е.
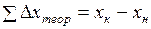 ;
; 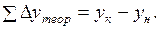 (1.21)
(1.21)
Для нашего примера
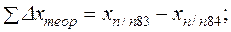
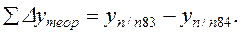
Так как измерения длин сторон имеют погрешности, то суммы вычисленных приращений ( 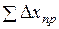 ,
, 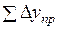 ) координат отличаются от теоретического значения. Разности этих величин называютневязками приращений.
) координат отличаются от теоретического значения. Разности этих величин называютневязками приращений. 
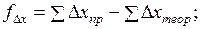
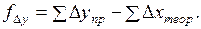 (1.22)
(1.22)
Невязки 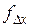 и
и 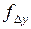 показывают отклонение вычисленных координат конечной точки от её теоретического положения соответственно по осям
показывают отклонение вычисленных координат конечной точки от её теоретического положения соответственно по осям 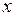 и
и 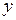 .
.
Для оценки точности используют линейную невязку, т.е. расстояние меж  ду этими точками (рис. 1.4). Линейную величину
ду этими точками (рис. 1.4). Линейную величину 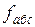 невязки определим как гипотенузу прямоугольного треугольника с катетами
невязки определим как гипотенузу прямоугольного треугольника с катетами 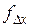 и
и 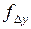 .
.
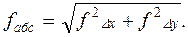 (1.23)
(1.23)
Наилучшим образом точность измерений в ходе характеризует относительная невязка, т.е. величина линейной невязки, отнесённая ко всему периметру полигона.
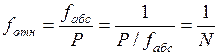 , (1.24)
, (1.24)
где
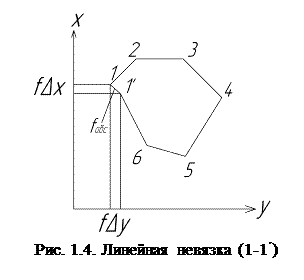
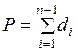 , (1.25)
, (1.25)
здесь п – число измерений сторон хода; Р – длина хода.
Относительную невязку принято записывать в виде дроби с единицей в числителе, что облегчает сравнение двух или нескольких значений. Качество измерений в теодолитном ходе считают удовлетворительным, если 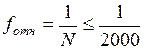 .
.
Если полученная относительная невязка не превышает допустимого значения, то невязки 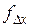 и
и 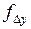 распределяют между приращениями координат.
распределяют между приращениями координат.
Примеры в задании подобраны так, чтобы относительная невязка получилась допустимой. Если относительная невязка оказалась недопустимой, то в вычислениях допущены ошибки.
Дирекционные углы сторон хода вычислены по исправленным значениям горизонтальных углов 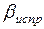 . Следовательно, появление невязок вызвано погрешностями измерения длин сторон хода. Кроме того, погрешность измерения стороны хода пропорциональна её длине (т.е. чем больше длина стороны, тем большая вероятность появления погрешности в её измерении), поэтому невязки в приращениях координат распределяют пропорционально длинам сторон, для этого в каждое приращение вычисляют поправку по формулам
. Следовательно, появление невязок вызвано погрешностями измерения длин сторон хода. Кроме того, погрешность измерения стороны хода пропорциональна её длине (т.е. чем больше длина стороны, тем большая вероятность появления погрешности в её измерении), поэтому невязки в приращениях координат распределяют пропорционально длинам сторон, для этого в каждое приращение вычисляют поправку по формулам
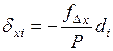 ;
; 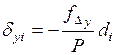 . (1.26)
. (1.26)
Контролем правильности распределения поправок являются равенства 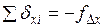 ;
; 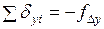 . Далее вычисляют исправленные значения приращений координат
. Далее вычисляют исправленные значения приращений координат
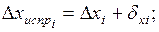
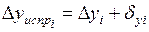 . (1.27)
. (1.27)
Контролем вычислений служит выполнение равенства
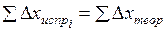 ;
; 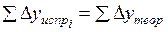 . (1.28)
. (1.28)
Для разомкнутого теодолитного хода
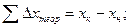
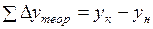 , (1.29)
, (1.29)
следовательно,
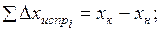
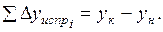 (1.30)
(1.30)
Вычисление координат точек теодолитного хода производят по формулам
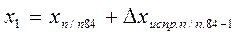 ; ;
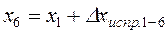 ;
……………………… ;
………………………
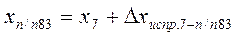 ; ;
| 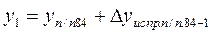 ; ;
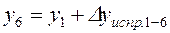 ;
………………………. ;
……………………….
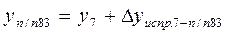 . .
|
Получение xп/п83и yп/п83, равных исходным значениям, служит контролем правильности вычисления координат точек теодолитного хода.
Дата добавления: 2016-01-09; просмотров: 1376;
