Основные определения. Известно, что в статически неопределимых стержневых конструкциях возникают напряжения в результате температурного воздействия
 Рис. 4.45. Температурные компенсаторы
Рис. 4.45. Температурные компенсаторы
|
Известно, что в статически неопределимых стержневых конструкциях возникают напряжения в результате температурного воздействия. Температурные напряжения особенно велики в стержне, защемленном по двум концам (см., например, решение задачи № 4 об определении температурных напряжений [5]). Для уменьшения температурных напряжений в такого рода конструкциях (например, в трубопроводах) используются температурные компенсаторы, которые увеличивают свободу деформаций за счет изгиба. Температурные компенсаторы представляют собой статически неопределимые рамы с двумя заделками по концам (рис. 4.45). В данном разделе рассматривается расчет плоских статически неопределимых рам (плоских трубопроводов) на температурное воздействие по методу упругого центра. Предполагается, что стержни рамы соединены между собой жестким образом под углом 90°, все стержни имеют одинаковую жесткость.
Рассматриваемые рамы являются три раза статически неопределимыми системами. Выберем основную систему для рамы, показанной на рис. 4.45, а, отбросив левую заделку (рис. 4.46). Лишними неизвестными являются реакции в защемлении: Х1, Х2 и Х3. В точке О поместим начало декартовой системы координат хОy. Положительное направление силы Х1 должно совпадать с направлением оси х, силы Х2 – с направлением оси y. Положительное направление пары сил Х3 должно соответствовать направлению поворота оси х к оси y. Можно показать, что решение канонической системы уравнений метода сил для выбранной основной системы дает такие формулы для определения лишних неизвестных:
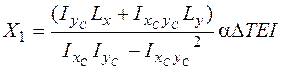 ; (4.30)
; (4.30)
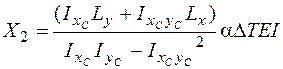 ; (4.31)
; (4.31)
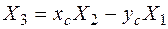 . (4.32)
. (4.32)
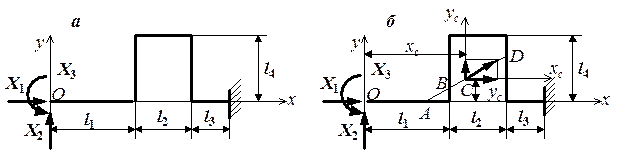 Рис. 4.46. К расчету трубопровода:
а – основная система;
б – точка С – упругий центр
Рис. 4.46. К расчету трубопровода:
а – основная система;
б – точка С – упругий центр
|
В этих формулах DТ – изменение температуры; a – коэффициент линейного температурного расширения; EI – жесткость стержней рамы; Lx, Ly – суммарные длины стержней рамы, параллельных осям х и y. При вычислении длины стержня учитывается направление обхода по длине стержня от начала координат. Если обход осуществляется по направлению оси, то длина участка рамы считается положительной, в противном случае – отрицательной. Например, для рамы, показанной на рис. 4.46, Ly = 0, так как обход левой стойки рамы от начала координат происходит по направлению оси y, а обход правой стойки – против направления оси.
Чтобы пояснить, что такое хс, yc, 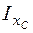 ,
, 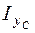 и
и 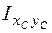 , будем рассматривать раму как плоскую фигуру, состоящую из прямоугольников. Одна сторона каждого прямоугольника равна длине участка рамы, а другая сторона (толщина) всегда равна 1. Например, рама на рис. 4.46 считается плоской фигурой, состоящей из пяти прямоугольников с длинами соответственно l1, l2, l3 и 2×l4и толщиной всех прямоугольников, равной 1. Тогда хс, yc – координаты центра тяжести этой плоской фигуры в системе координат xОy. Центр тяжести фигуры (точка С на рис. 4.46, б) называется упругим центром. Через упругий центр проведем центральные оси xc, yc, параллельные осям x, y. В формулах (4.30), (4.31)
, будем рассматривать раму как плоскую фигуру, состоящую из прямоугольников. Одна сторона каждого прямоугольника равна длине участка рамы, а другая сторона (толщина) всегда равна 1. Например, рама на рис. 4.46 считается плоской фигурой, состоящей из пяти прямоугольников с длинами соответственно l1, l2, l3 и 2×l4и толщиной всех прямоугольников, равной 1. Тогда хс, yc – координаты центра тяжести этой плоской фигуры в системе координат xОy. Центр тяжести фигуры (точка С на рис. 4.46, б) называется упругим центром. Через упругий центр проведем центральные оси xc, yc, параллельные осям x, y. В формулах (4.30), (4.31) 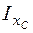 ,
, 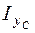 и
и 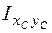 – осевые и центробежный моменты инерции рассматриваемой плоской фигуры относительно центральных осей xc, yc.
– осевые и центробежный моменты инерции рассматриваемой плоской фигуры относительно центральных осей xc, yc.
Напомним некоторые формулы. Координаты центра тяжести плоской фигуры находим так:
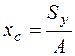 ;
; 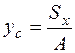 , (4.33)
, (4.33)
где А – площадь фигуры. В данном случае, так как толщина всех прямоугольников равна единице, площадь равна сумме длин всех участков рамы. Для рамы на рис. 4.46 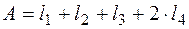 ; Sx, Sy – статические моменты фигуры относительно осей x, y, которые находятся как суммы статических моментов каждого прямоугольника относительно осей x, y. Статический момент каждого прямоугольника равен произведению площади прямоугольника на координату центра тяжести прямоугольника в системе координат хОy.
; Sx, Sy – статические моменты фигуры относительно осей x, y, которые находятся как суммы статических моментов каждого прямоугольника относительно осей x, y. Статический момент каждого прямоугольника равен произведению площади прямоугольника на координату центра тяжести прямоугольника в системе координат хОy.
Моменты инерции плоской фигуры вычисляются как суммы моментов инерции простых фигур, составляющих данную фигуру, в рассматриваемом случае момент инерции всей фигуры равен сумме моментов инерций прямоугольников единичной толщины. Для каждого прямоугольника справедливы формулы
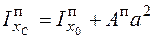 ; (4.34)
; (4.34)
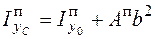 ; (4.35)
; (4.35)
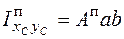 , (4.36)
, (4.36)
где 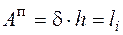 – площадь прямоугольника (
– площадь прямоугольника (  ,
,  ); a, b – координаты центра тяжести прямоугольника в системе координатных осей xc, yc;
); a, b – координаты центра тяжести прямоугольника в системе координатных осей xc, yc; 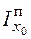 ,
, 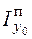 – моменты инерции прямоугольника относительно собственных центральных осей x0, y0, параллельных осям xc, yc. Если ось x0 (или y0) расположена вдоль рассматриваемого участка трубопровода, то есть параллельна стороне прямоугольника li, то можно считать
– моменты инерции прямоугольника относительно собственных центральных осей x0, y0, параллельных осям xc, yc. Если ось x0 (или y0) расположена вдоль рассматриваемого участка трубопровода, то есть параллельна стороне прямоугольника li, то можно считать 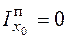 (или
(или 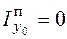 ). Если же ось x0 (или y0) перпендикулярна стороне li, то
). Если же ось x0 (или y0) перпендикулярна стороне li, то 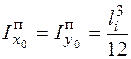 . В формуле (4.36) учтено, что центробежный момент инерции прямоугольника
. В формуле (4.36) учтено, что центробежный момент инерции прямоугольника 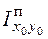 относительно собственных осей x0, y0 равен нулю, так как эти оси являются главными осями инерции прямоугольника.
относительно собственных осей x0, y0 равен нулю, так как эти оси являются главными осями инерции прямоугольника.
После определения величин лишних неизвестных по формулам (4.30) – (4.32) строим эпюры внутренних усилий в основной системе, как в обычной статически определимой раме. Эпюру изгибающих моментов можно проверить следующим образом. В упругом центре приложим найденные силы Х1 и Х2, нарисовав их в масштабе. Определим графически равнодействующую этих сил. Точки пересечения линии действия этой равнодействующей с осью рамы – это точки, в которых изгибающий момент должен равняться нулю (точки A, B, D на рис. 4.46, б).
Построив эпюры внутренних усилий, проверим прочность конструкции, имея в виду, что поперечное сечение стержней рамы – труба и, кроме температурного воздействия, труба испытывает действие внутреннего давления. Максимальные нормальные напряжения sх, действующие на площадках, перпендикулярных оси трубы, находим, складывая напряжения от продольной силы и максимального изгибающего момента в опасном сечении рамы[13]:
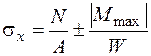 . (4.37)
. (4.37)
Для проверки прочности трубы из пластичного материала по формуле (4.37) находим максимальное по модулю напряжение. Если труба выполнена из хрупкого материала, при проверке прочности важен знак напряжений. Кольцевое напряжение sq , возникающее от внутреннего давления q, определяем по формуле
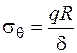 , (4.38)
, (4.38)
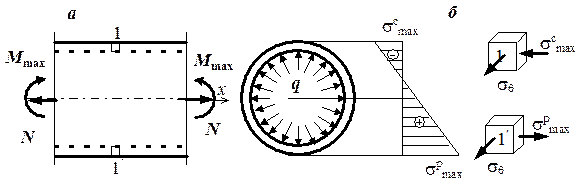 Рис. 4.47. К определению напряжений в трубе:
а – распределение напряжений sх в опасном сечении;
б – напряженное состояние опасных точек
Рис. 4.47. К определению напряжений в трубе:
а – распределение напряжений sх в опасном сечении;
б – напряженное состояние опасных точек
|
где R и d – соответственно внешний радиус и толщина трубы. Напряжение sq всегда растягивающее. На рис 4.47, а показана эпюра распределения напряжений sх в опасном сечении при положительной продольной силе. Рис. 4.47, б изображает напряженное состояние опасных точек 1, 1¢. Так как касательные напряжения на площадках элементов, показанных на рис. 4.47, б, отсутствуют, то эти площадки являются главными. Проверку прочности в опасных точках осуществляем по теории прочности, соответствующей материалу трубы.
Пример расчета трубопровода (задача № 26)
Условие задачи
Трубопровод, показанный на рис. 4.48, а, нагревается на DТ градусов и подвержен действию внутреннего давления q. Труба имеет внешний радиус поперечного сечения R и толщину d. Известен материал трубы. Требуется найти напряженное состояние и обеспечить выполнение условия прочности трубопровода.
Решение
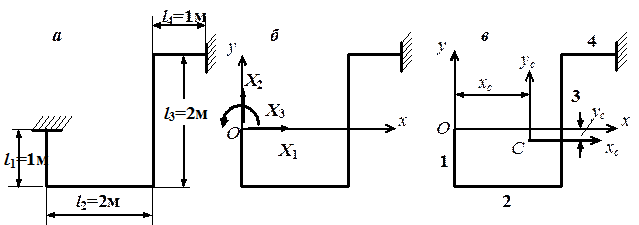 Рис. 4.48. К примеру расчета трубопровода: а – заданная система;
б – основная система;
в – положение упругого центра
Рис. 4.48. К примеру расчета трубопровода: а – заданная система;
б – основная система;
в – положение упругого центра
|
Выберем основную систему, отбросив левое закрепление и приложив реактивные силы (лишние неизвестные) Х1, Х2 и Х3 (рис. 4.48, б). Для определения значений лишних неизвестных по формулам (4.30) – (4.32) найдем сначала положение упругого центра и геометрические характеристики 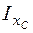 ,
, 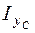 и
и 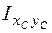 .
.
Координаты упругого центра в системе координат xОy сосчитаем по формулам (4.33), где
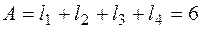 м.
м.
Статический момент относительно оси х равен сумме статических моментов четырех прямоугольников единичной толщины:
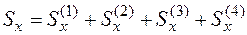 .
.
Статический момент третьего участка трубопровода (третьего прямоугольника) 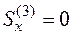 , так как центр тяжести этого прямоугольника лежит на оси х, а статические моменты остальных прямоугольников найдем следующим образом:
, так как центр тяжести этого прямоугольника лежит на оси х, а статические моменты остальных прямоугольников найдем следующим образом:
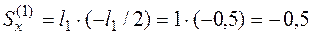 м2,
м2,
где 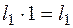 – площадь первого прямоугольника, а (–
– площадь первого прямоугольника, а (– 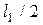 ) – координата центра тяжести. Аналогично
) – координата центра тяжести. Аналогично
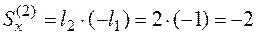 м2,
м2,
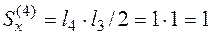 м2.
м2.
Таким образом,
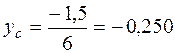 м.
м.
Вторая координата упругого центра
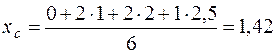 м.
м.
Отложим эти координаты на рисунке и покажем точку С – упругий центр. Проведем через точку С центральные оси xc, yc (рис. 4.48, в). Найдем моменты инерции фигуры относительно этих осей. Момент инерции относительно оси хс равен сумме моментов инерции четырех прямоугольников:
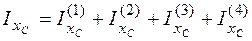 .
.
Сосчитаем момент инерции первого прямоугольника относительно оси хс по формуле (4.34). Для рассматриваемого прямоугольника собственная ось х0 перпендикулярна стороне l1, поэтому первый член в (4.34) (момент инерции первого прямоугольника собственной оси х0 ) не равен нулю. Таким образом, момент инерции относительно оси хс
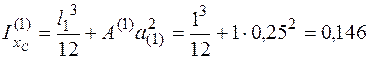 м3.
м3.
Для второго прямоугольника момент инерции относительно
оси хс
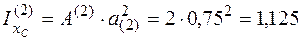 м3.
м3.
Поскольку ось х0 параллельна стороне прямоугольника l2, то первое слагаемое в формуле (4.34) отсутствует ( 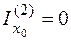 ). Аналогично находим моменты инерции остальных прямоугольников:
). Аналогично находим моменты инерции остальных прямоугольников:
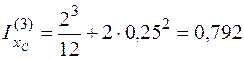 м3;
м3;
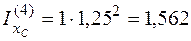 м3.
м3.
И полный момент инерции относительно оси хс равен 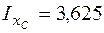 м3. Так же вычислим момент инерции относительно оси yc каждого прямоугольника:
м3. Так же вычислим момент инерции относительно оси yc каждого прямоугольника:
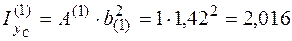 м3;
м3;
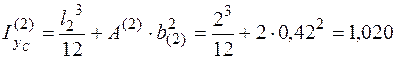 м3;
м3;
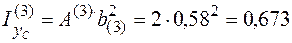 м3;
м3;
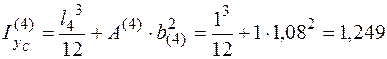 м3.
м3.
Полный момент инерции относительно оси yc равен сумме моментов инерции всех прямоугольников 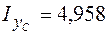 м3.
м3.
Найдем центробежный момент инерции. Момент инерции каждого прямоугольника определим по формуле (4.36). Обратим внимание на то, что, если при вычислении осевых моментов инерции знаки координат а и b можно опускать, так как они входят в формулы (4.34), (4.35) в квадрате, то при вычислении центробежного момента инерции эти знаки следует обязательно учитывать. Тогда
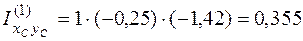 м3;
м3;
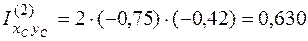 м3;
м3;
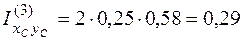 м3;
м3;
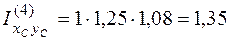 м3.
м3.
Полный центробежный момент инерции 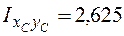 м3.
м3.
Длины трубопровода вдоль осей х и y: 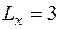 м,
м, 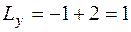 м. Подставляя найденные геометрические характеристики в формулы (4.30)–(4.32), сосчитаем значения лишних неизвестных:
м. Подставляя найденные геометрические характеристики в формулы (4.30)–(4.32), сосчитаем значения лишних неизвестных:
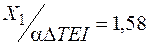 м–2;
м–2;
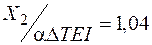 м–2;
м–2;
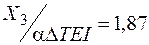 м–1.
м–1.
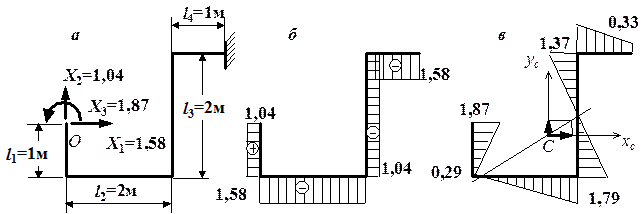 Рис. 4.49. Определение внутренних усилий в трубопроводе:
а – основная система с найденными реакциями в долях от aDTЕI;
б – эпюра продольных сил N в долях от aDTЕI;
в – эпюра изгибающих моментов М в долях от aDTЕI
Рис. 4.49. Определение внутренних усилий в трубопроводе:
а – основная система с найденными реакциями в долях от aDTЕI;
б – эпюра продольных сил N в долях от aDTЕI;
в – эпюра изгибающих моментов М в долях от aDTЕI
|
Нарисуем основную систему и приложим в точке О найденные опорные реакции. Так как все лишние неизвестные оказались положительными, то сохраняем выбранное ранее направление всех неизвестных (рис. 4.49, а). Построим эпюры продольных сил и изгибающих моментов в долях от  (рис. 4.49, б, в). На рис. 4.49, в показана равнодействующая сил Х1 и Х2, приложенных в упругом центре. Видно, что на линии действия этой равнодействующей изгибающий момент равен нулю.
(рис. 4.49, б, в). На рис. 4.49, в показана равнодействующая сил Х1 и Х2, приложенных в упругом центре. Видно, что на линии действия этой равнодействующей изгибающий момент равен нулю.
Теперь можно решать вопрос о проверке прочности трубы. По эпюрам N и М находим опасное сечение. У нас это сечение в точке О (рис. 4.49, а). [14] В этом сечении действуют одновременно максимальный изгибающий момент и растягивающая продольная сила:  ,
,  . Напряжения в опасных точках вычисляем по формулам (4.37) и (4.38). Для удобства расчетов приведем формулу (4.37) к другому виду. Максимальное напряжение от изгиба
. Напряжения в опасных точках вычисляем по формулам (4.37) и (4.38). Для удобства расчетов приведем формулу (4.37) к другому виду. Максимальное напряжение от изгиба
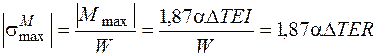 ,
,
так как момент сопротивления 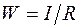 . Нормальное напряжение, вызванное продольной силой, найдем так:
. Нормальное напряжение, вызванное продольной силой, найдем так:
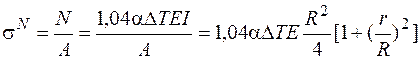 ,
,
где учтено, что для трубы
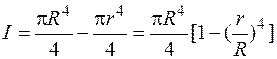 ,
, 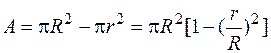 ,
,
r – внутренний радиус трубы. Суммарные напряжения на площадках, перпендикулярных оси х, находим согласно (4.37), складывая sN и 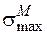 .
.
Отметим особенность решаемой задачи об определении температурных напряжений в статически неопределимой раме: чем больше размер поперечного сечения (больше радиус трубы), тем больше возникающие в конструкции температурные напряжения. Это связано с тем, что с увеличением радиуса увеличивается жесткость рамы и уменьшается свобода деформаций, что и приводит к увеличению напряжений.
Вычисляя напряжения в опасных точках, обратите внимание на единицы измерения величин, входящих в формулы для напряжений. В формуле для определения 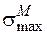 число 1,87 имеет размерность м–1, в формуле для
число 1,87 имеет размерность м–1, в формуле для 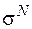 число 1,04 измеряется в м–2. Таким образом, подставляя R в метрах, получим величину напряжения в тех же единицах измерения, что и модуль упругости Е. При проверке прочности в опасных точках трубы используйте знания, полученные при изучении разд. 2 "Исследование плоского напряженного состояния. Проверка прочности для сложного напряженного состояния" [5]. Если условие прочности выполняться не будет, следует уменьшить радиус трубы и добиться удовлетворения условия прочности.
число 1,04 измеряется в м–2. Таким образом, подставляя R в метрах, получим величину напряжения в тех же единицах измерения, что и модуль упругости Е. При проверке прочности в опасных точках трубы используйте знания, полученные при изучении разд. 2 "Исследование плоского напряженного состояния. Проверка прочности для сложного напряженного состояния" [5]. Если условие прочности выполняться не будет, следует уменьшить радиус трубы и добиться удовлетворения условия прочности.
Дата добавления: 2016-01-09; просмотров: 849;
