Основные определения. Статически определимая рама – конструкция, состоящая из нескольких изгибаемых стержней, закрепленных так
Статически определимая рама – конструкция, состоящая из нескольких изгибаемых стержней, закрепленных так, что опорные реакции и внутренние усилия можно найти с помощью уравнений статики. Чаще всего стержни рамы соединены между собой жестким образом, так, что в процессе деформации угол между стержнями не меняется. Мы будем рассматривать только плоские рамы, стержни которых расположены под углом 90°. Вертикальные стержни рамы принято называть стойками, горизонтальные – ригелями. В стержнях плоских рам возникают три внутренних усилия: продольная и поперечная силы и изгибающий момент.
Внутренние усилия в рамах определяются методом сечений, и порядок их нахождения тот же, что и для балок. Напомним, что согласно методу сечений:
* продольная сила N равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось стержня;
* поперечная сила Q равна сумме проекций всех сил, действующих с одной стороны от сечения, на ось, перпендикулярную оси стержня;
* изгибающий момент M равен сумме моментов всех сил, действующих с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения.
Правила знаков для продольной и поперечной сил те же, что и раньше: растягивающая продольная сила положительна, поперечная сила положительна, если она обходит сечение по ходу часовой стрелки. Правило знаков для изгибающего момента в рамах следующее: момент считается положительным, если он изгибает стержень рамы выпуклостью вовнутрь[10]. На эпюрах N и Q положительные значения принято откладывать снаружи, на эпюре М – внутри – со стороны растянутых волокон.
От действия трех внутренних усилий в стержнях рамы возникают напряжения: нормальные и касательные. Нормальные напряжения определяются как сумма напряжений от продольной силы ( 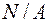 ) и от изгибающего момента по формуле (4.1). Касательные напряжения находят по формуле Журавского (4.2).
) и от изгибающего момента по формуле (4.1). Касательные напряжения находят по формуле Журавского (4.2).
Перемещения точек оси рамы определяются, как правило, методом Максвелла – Мора по формуле (4.21). Заметим, что произвольная точка оси рамы в отличие от точки оси балки может перемещаться не только по вертикали, но и по горизонтали. Будем обозначать линейные перемещения точек оси рамы буквой d, отмечая направление перемещения индексом сверху: dверти dгор. Углы поворота сечений рамы, как и балок, обозначаем буквой j.
Дата добавления: 2016-01-09; просмотров: 814;
