Функции таблиц смертности

Интервал возраста (х, х+n) пет	Числа доживающих до точного возраста х пет, I*	Вероятность умереть на интервале возраста (х, х+n) лет, _nq_x	Вероятность остаться в живых на интервале возраста (х, х+n) лет, _nР_x	Числа умирающих на интервале возраста (х, х+n) лет, _nd_x	Доля последнего года жизни для умирающих на интервале возраста (х, х+n) пет, _na'_x	Числа живущих на интервале возраста (х, х+n) лет, _nL_x	Число человеко-лет, прожитых после достижения точного возраста х лет, T_х	Средняя ожидаемая продолжительность предстоящей жизни в возрасте х лет, ^л_x
					6			9
0-1	100 000	_nd_x/l_x	1 - _nq_x	l_x*_nq_x		(l_x_-_nd_x)+_„а '_x *_nd_x	S,,L_n	T_x/l_x
1-2	100000-d₀				.43
2-3	l_x=l_x-1-_nd_x				.45
3-4					.47
4-5					.49
5-ö					.50

возрастной интервал (х, х + 1) лет, вносит в общее число человеко-лет (/_r- d_x) лет. Каждый же из тех, кто умрет на этом интервале возраста, вносит в L_x в среднем а '_х часть этого интервала. Отсюда: L_x - (l_x-d_x)'+ а'_х- d_x (х = О,1, 2- 1). В полных таблицах смертности в возрастах 5 лет и старше величина а '_х принимается равной 1/2 и, поэтому, для этих возрастов L_x - полными аналогами среднегодового населения.

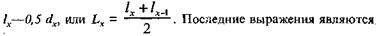
Графа 8.Число человеко-лет, которое предстоит прожить после достижения точного возраста х лет, Т_x Это число равно сумме человеко-лет, прожитых в каждом возрастном интервале начиная с возраста х лет, или Т_х = L_x.

Графа 9.Средняя ожидаемая продолжительность предстоящей жизни в возрасте х лет, е^л_х. Это число показывает, сколько в среднем предстоит прожить человеку, достигшему возраста х лет. Поскольку всем дожившим до этого возраста (их число равно l_x предстоит прожить Т_х лет, постольку е^л_х=T_x/l_x , лет.

Каждое е^л_х суммирует смертность в возрастах старше x лет, что делает эту графу наиболее важной в таблице смертности. Более того, это одна из трех функций таблицы смертности (наряду с q_x и а'_х), которая имеет смысл безотносительно к корню таблицы. Как правило, е^л_х убывает с возрастом. Единственное исключение представляет собой возраст 0 лет, когда е^л₀< e^л₁ из-за высокой младенческой смертности. Это называется парадоксом младенческой смертности. В высокоразвитых странах с очень низкими значениями младенческой смертности этот парадокс не действует.

<64 65 666768 69 70 >

Дата добавления: 2016-01-09; просмотров: 784;