Виды степенных средних

Вид степенной средней	Показатель степени (m)	Формула расчета
Простая	Взвешенная
Гармоническая	-1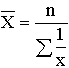
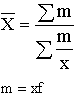
Геометрическая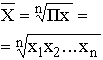
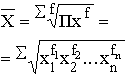
Арифметическая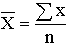
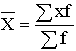
Квадратическая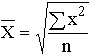
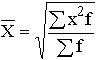
Кубическая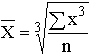

Средняя геометрическая применяется, когда имеется n коэффициентов роста, при этом индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики. Средняя характеризует, таким образом, средний коэффициент роста. Средняя геометрическая простая рассчитывается по формуле

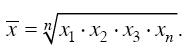
Формула средней геометрической взвешенной имеет следующий вид:

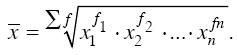
Приведенные формулы идентичны, но одна применяется при текущих коэффициентах или темпах роста, а вторая – при абсолютных значениях уровней ряда.

Средняя квадратическая применяется при расчете с величинами квадратных функций, используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения и вычисляется по формуле

Средняя квадратическая взвешенная рассчитывается по другой формуле:

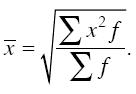
Средняя кубическая применяется при расчете с величинами кубических функций и вычисляется по формуле

средняя кубическая взвешенная:

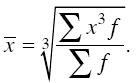
Все рассмотренные выше средние величины могут быть представлены в виде общей формулы:

где 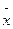– средняя величина; х– индивидуальное значение; n – число единиц изучаемой совокупности; k – показатель степени, определяющий вид средней.

При использовании одних и тех же исходных данных, чем больше k в общей формуле степенной средней, тем больше средняя величина. Из этого следует, что между величинами степенных средних существует закономерное соотношение:

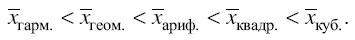
Для иллюстрации мажорантности рассмотрим пример.

Студент ВУЗа получил в течение семестра всего две оценки: "3" и "2". Требуется рассчитать степенные средние всех видов и с их помощью проверить действие правила мажорантности.

1) 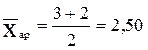(балла)

2) 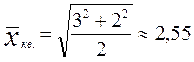(балла)

3) (балла)

4) 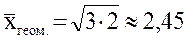(балла)

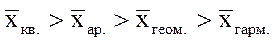
2,55 > 2,50 > 2,45 > 2,41