ФИЗИЧЕСКАЯ СУЩНОСТЬ ЭФФЕКТА ДЖОЗЕФСОНА

Сверхпроводящее токовое состояние отличается от токового состояния в несверхпроводящем металле своей устойчивостью по отношению к рассеянию носителей тока на разного рода дефектах. Благодаря этому становится возможным существование незатухающих токов в сверхпроводниках, содержащих примеси посторонних элементов или другого рода дефекты. Наличие примесей не препятствует установлению макроскопической когерентности сверхпроводящего состояния, несмотря на то, что даже при малых концентрациях примесей (например, –1%) среднее расстояние между ними составляет несколько межатомных расстояний и поэтому мало по сравнению с параметром сверхпроводящей корреляции — характерным размером куперовской пары 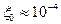см.

Термин макроскопическая когерентность сверхпроводящего состояния означает, что сверхпроводящее тело как целое характеризуется некоторой комплексной функцией

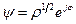, (36)

имеющей смысл волновой функции куперовской пары и отличной от нуля ниже точки сверхпроводящего перехода, здесь r – плотность частиц, характеризующих сверхпроводящее состояние, j – общая фаза частиц. Причем r в сверхпроводящем состоянии связана с модулем y – функции:

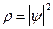. (37)

Функция y была впервые введена в теорию Гинзбургом и Ландау, как параметр упорядочения теории сверхпроводимости. Временное изменение функции y определяется уравнением квантовой механики

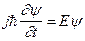. (38)

Величина E равна удвоенному значению электрохимического потенциала m, эта величина равна минимальной энергии, которую надо затратить на добавление к системе одной куперовской пары. Таким образом, y – функция, являющаяся решением (38), имеет вид:

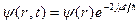. (39)

Поскольку число куперовских пар N и фаза j – канонически сопряженные переменные, для них выполняется соотношение неопределенностей в виде:

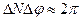. (40)

Следовательно, в случае изолированного сверхпроводника (N фиксировано) фаза j неопределенна.

Наличие единой для всего образца y – функции, характеризующей не только одну частицу, но и весь коллектив электронов, влечет за собой возникновение фиксированных (в данный момент времени) разностей фаз y – функции в любых двух точках сверхпроводника, удаленных друг от друга на большие (макроскопические) расстояния – фактически во всем объеме сверхпроводящего тела. Такая когерентность фазы приводит к целому ряду специфических квантовых эффектов.

Существенно отметить, что когерентность фазы является общим свойством сверхпроводников, не зависящим от их конкретной структуры. Градиент y – функции определяет величину протекающего в сверхпроводнике тока. Фиксированному значению градиента фазы Ñj отвечает ток, равный

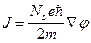, (41)

где N_s — так называемое "число сверхпроводящих электронов".

В сверхпроводящем сплаве когерентность фазы не исчезает, несмотря на наличие дефектов, расстояние между которыми может быть существенно меньше параметра 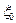. Можно сказать, что линии сверхпроводящего тока (линии градиента фазы Ñj) огибают препятствия или проходят через них, так что наличие дефектов не препятствует установлению фазовой когерентности.

Описанная ситуация, касающаяся однородных систем, хорошо известна. Такое же свойство сохраняется и для систем, не являющихся однородными. Рассмотрим плоский слой примесных атомов в чистом сверхпроводнике. Свойство фазовой когерентности будет иметь место, однако градиент фазы уже не будет постоянным: изменение фазы при пересечении плоскости, в которой расположены примеси, будет более быстрым. чем в остальной части сверхпроводника (считаем, что ток течет однородно). Действительно, величина N_s в формуле (41) уменьшается с увеличением числа дефектов. Так, для предельно грязного сплава с 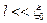(l – длина свободного пробега) она равна 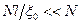, т.е. значительно меньше соответствующего значения концентрации для чистого сверхпроводника.

Оказывается, что свойство фазовой когерентности сохраняется также в том случае, когда вместо слоя примесных атомов вблизи плоскости z = 0 расположена достаточно тонкая пленка диэлектрика. В этом случае электроны также могут переходить из левой области в правую (и наоборот) посредством квантово–механического туннельного эффекта благодаря чему этот случай принципиально не отличается от разобранного выше. Вследствие этого сверхпроводящий ток может протекать через достаточно тонкий диэлектрический зазор. Это свойство обычно называют стационарным эффектом Джозефсона.

Таким образом, макроскопическая когерентность сверхпроводящего состояния характерная для однородных сверхпроводников, сохраняется также в том случае, когда сверхпроводник представляет собой сложную систему, составленную из двух частей, разделенных достаточно тонкой непроводящей (или несверхпроводящей) прослойкой. При этом протекание сверхпроводящего тока через такую прослойку сопровождается появлением скачка фазы на барьере. Поскольку ток сверхпроводящий, разность потенциалов на барьере отсутствует. Подобно тому, как в однородном сверхпроводнике величина тока пропорциональна градиенту фазы Ñj, в данном случае сверхпроводящий ток оказывается зависящим от величины разности фаз на барьере j = j₁ –j₂.

Сверхпроводящий туннельный ток Джозефсона переносится куперовскими парами. Величина тока Джозефсона пропорциональна вероятности туннелирования не для пары, а для отдельного электрона: сверхпроводящий ток Джозефсона оказывается того же порядка величины, что и нормальный туннельный ток. Это связано с тем, что туннелирование в эффекте Джозефсона представляет сложный процесс, идущий через промежуточное состояние, в котором пары диссоциированы, благодаря чему коэффициент прозрачности барьера имеет по порядку величины то же значение, что и для нормального металла.

Нестационарный эффект Джозефсона заключается в том, что при отличной от нуля постоянной разности потенциалов на барьере сверхпроводящий туннельный ток (ток куперовских пар) становится переменным во времени, причем частота его осцилляции связана с разностью потенциалов соотношением

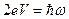. (42)

Величина 2eV представляет разность энергий куперовской пары в левом и правом металлах (2е — заряд пары). Поэтому в данном случае туннелирование пары происходит с изменением ее энергии на величину 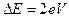, 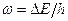– классическая частота перехода.

Пусть связанная куперовская пара электронов обладает набором состояний 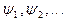с различными значениями энергии 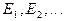. Пусть, далее, под действием некоторого возмущения V происходят переходы между этими состояниями. Если в начальный момент времени (t = 0) система находилась в каком–то определенном состоянии (например 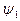), то, согласно нестационарной теории возмущений, вероятность пребывания ее к моменту времени t>0 в состоянии 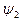будет описываться формулой

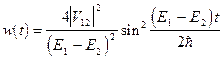. (43)

Следовательно, вероятность пребывания системы в состоянии 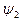есть осциллирующая функция времени с частотой 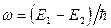. Переход в состояние с другой энергией не противоречит закону сохранения энергии, так как неопределенность энергии составляет при этом 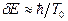, где 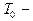период осцилляций, т. е. является величиной того же порядка, что изменение энергии при переходе.

Туннелирование куперовской пары при наличии разности потенциалов на барьере есть квантовый переход между состояниями с различной энергией ( 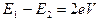). Отсюда следует, что частота перехода описывается формулой Джозефсона (42). Движение отдельных куперовских пар не является независимым. Они образуют макроскопическую квантовую систему – конденсат; при этом фазы волновых функций куперовских пар (и вообще все переменные, характеризующие состояние их движения как целого) в точности совпадают. Поэтому квантовые осцилляции туннельного тока, аналогичные рассмотренным выше осцилляциям вероятности перехода, происходят в макроскопическом масштабе. Приведенное рассуждение имеет смысл аналогии, позволяющей понять физическую природу эффекта Джозефсона.

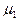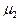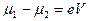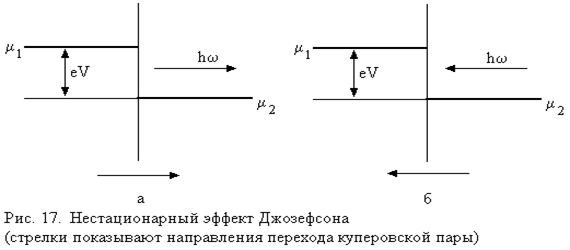
Соотношение (42) может быть также объяснено следующим образом. При отличной от нуля разности потенциалов V куперовские пары в металлах 1 и 2 сконденсированы каждая на своем уровне Ферми и , причем (рис. 17). Переходы между этими уровнями при наличии взаимодействия с полем излучения могут сопровождаться испусканием фотонов с частотой 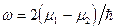. (рис. 17, а). Соотношение (42) в этом случае выражает закон сохранения энергии для соответствующего процесса. Возможен также обратный переход, связанный с поглощением фотона и переходом пары на более высокий уровень (рис. 17, б).

Мы можем описывать макроскопическую систему (сверхпроводник) переходами для одной куперовской пары, так как движение всех пар в сверхпроводнике полностью идентично в силу их подчинения распределению Бозе. По той же причине излучение, показанное на рис. 1, должно быть не только монохроматическим, но и когерентным.