Основы теории подобия лопастных насосов
Процессы, происходящие в лопастных насосах, в связи с их чрезвычайной сложностью не поддаются достаточному удовлетворительному теоретическому описанию, поэтому невозможно получить расчетные формулы теоретическим способом.
При проектировании новых насосов широко используют так называемые формулы подобия, полученные на основе теории подобия гидравлических явлений.
В основу теории подобия гидравлических явлений положены условия геометрического, кинематического и динамического подобия.
Для лопастных насосов условие геометрического подобия означает пропорциональность всех сходственных геометрических размеров проточной части, а также равенство конструктивных углов лопаток и одинаковое их число:
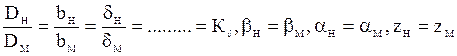 ,
,
где  – размеры, углы и число лопаток натурного насоса;
– размеры, углы и число лопаток натурного насоса;
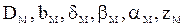 – то же для модельного насоса;
– то же для модельного насоса;
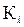 – коэффициент геометрического подобия, масштаб моделирования.
– коэффициент геометрического подобия, масштаб моделирования.
Кинематическое подобие имеет место, если отношения скоростей, приложенных в сходственных точках, равны. Отсюда следует подобие треугольников скоростей в сходственных точках натурного и модельного насосов (рисунок 3.18).
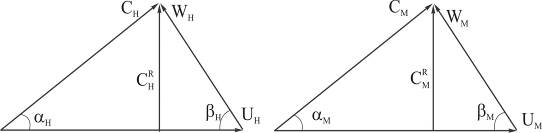
Рисунок 3.18
Из подобия треугольников следует:
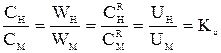 ;
;
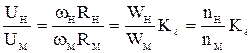 ,
,
где 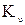 - масштаб кинематического подобия.
- масштаб кинематического подобия.
Условием динамического подобия является пропорциональность всех сил, приложенных в сходственных точках натурного и модельного насосов. Для гидромеханического процесса в лопастных насосах превалирующими силами являются инерционные силы и силы:
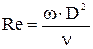 ,
, 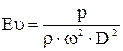 .
.
Лопастные насосы обычно работают при значительных числах  , и влияние сил вязкости на поток уменьшается.
, и влияние сил вязкости на поток уменьшается.
Критерий Эйлера будет сохраняться постоянным, если насос работает на одном режиме (р = const).
Из условия подобия устанавливается связь между основными показателями работы натурного и модельного насоса, работающих на одинаковых режимах, определяемых КПД насоса.
Рассмотрим подачу насоса.
Для натурного насоса подача составит 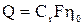 . Для модели
. Для модели 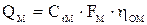 . Пренебрегаем разницей
. Пренебрегаем разницей 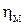 и
и 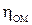 , сравним подачи насосов:
, сравним подачи насосов:
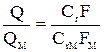 .
.
Из условия геометрического и кинематического подобия имеем:
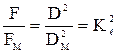 и
и 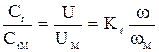 , т.е.
, т.е. 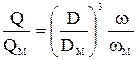 или
или 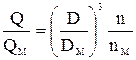 .
.
Из полученных уравнений вытекает
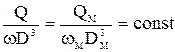 .
.
Безразмерный комплекс 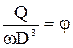 называется коэффициентом подачи.
называется коэффициентом подачи.
Напор насоса может быть представлен формулой Эйлера с учетом конечного числа лопаток k и гидравлических потерь:
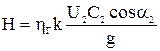 .
.
Принимая 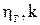 одинаковыми для натурного насоса и модели, устанавливают соотношение напоров:
одинаковыми для натурного насоса и модели, устанавливают соотношение напоров:
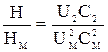 или
или 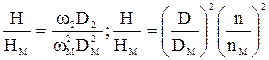 .
.
Полученная формула дает возможность получить безразмерный комплекс, называемый коэффициентом напора:
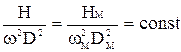 .
.
Умножая числители соотношений на g, получаем 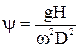 .
.
Мощности натурного насоса и модели относятся между собой следующим образом:
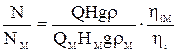 ,
,
где 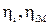 - внутреннее КПД насосов.
- внутреннее КПД насосов.
Одинаковые режимы работы предполагают постоянство внутренних КПД 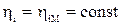 , тогда при
, тогда при 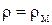 получается соотношение
получается соотношение
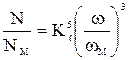 или
или 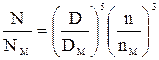 .
.
Все лопастные насосы принято делить по геометрическим формам на несколько групп. Каждая группа подобных насосов, или, как ее называют, серия подобных насосов, имеет общий масштаб моделирования.
Серию подобных насосов характеризует одинаковый для всех насосов коэффициент быстроходности. Насосы с равными 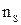 не обязательно подобны, т.к. в формуле для
не обязательно подобны, т.к. в формуле для 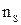 не содержатся требования геометрического подобия.
не содержатся требования геометрического подобия.
По величине 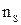 можно судить о конструкции рабочего колеса.
можно судить о конструкции рабочего колеса.
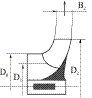
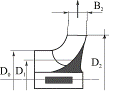
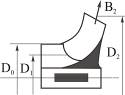
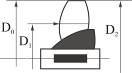
В таблице 3.1 приводятся меридиональные сечения рабочих колес, имеющих различные 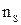 , соотношения диаметров колеса и входного патрубка.
, соотношения диаметров колеса и входного патрубка.
При малых 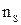 колеса тихоходные, межлопаточный канал колеса узкий и длинный. С увеличением
колеса тихоходные, межлопаточный канал колеса узкий и длинный. С увеличением 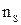 канал становится шире, диаметры входа и выхода сближаются между собой, поток жидкости меняет свое направление. Так, в центробежных насосах поток перемещается перпендикулярно оси вала (колесо радиальное), в диагональном насосе поток движется по наклонной к оси, в осевом насосе – параллельно оси вала.
канал становится шире, диаметры входа и выхода сближаются между собой, поток жидкости меняет свое направление. Так, в центробежных насосах поток перемещается перпендикулярно оси вала (колесо радиальное), в диагональном насосе поток движется по наклонной к оси, в осевом насосе – параллельно оси вала.
Значение коэффициента быстроходности можно оценить следующим образом.
1 При одном и том же числе оборотов вала насоса увеличение 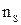 свидетельствует об увеличении подачи и уменьшении напора насоса.
свидетельствует об увеличении подачи и уменьшении напора насоса.
2 Тихоходные колеса служат для создания больших напоров, колеса с большими 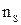 - для создания большой подачи.
- для создания большой подачи.
3 У центробежных насосов общий КПД меняется в зависимости от 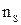 (рисунок 3.19).
(рисунок 3.19).
Таблица 3.1
| Виды колес | Центробежные насосы | Колесо диагонального насоса | Колесо осевого насоса | ||
| тихоходные | нормальные | быстроходные | |||
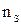
| 40-80 | 80-150 | 150-300 | 300-600 | 600-1200 |
| Форма колеса | 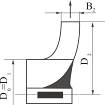
| 
|
|
|
|
| D2/D0 | 2,5 | 1,8-1,4 | 1,2-1,1 | 0,8 |

Рисунок 3.19
Наиболее выгодно выполнять насосы с 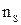 =90-300. Тихоходные колеса имеют низкий КПД за счет больших гидравлических потерь в каналах рабочих колес.
=90-300. Тихоходные колеса имеют низкий КПД за счет больших гидравлических потерь в каналах рабочих колес.
4 Насосы с различными коэффициентами быстроходности имеют особенности в форме рабочих характеристик.
Для сравнения удобно воспользоваться относительными характеристиками, которые отличаются тем, что все показатели работы насосов (независимо от их коэффициента быстроходности) взяты относительно оптимального режима, принятого за единицу (или за 100% - процентные характеристики).
Такие характеристики для насосов с разными 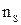 представлены на рисунке 3.20 (а, б, в).
представлены на рисунке 3.20 (а, б, в).
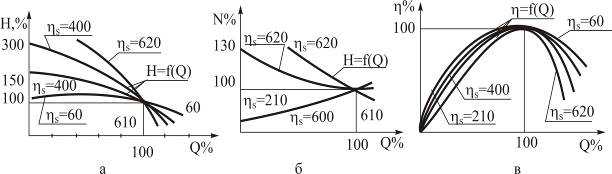
Рисунок 3.20
Из рисунков 3.20, а, б видно, что с увеличением 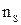 характеристики напора и мощности становятся все более крутопадающими, а из рисунка 3.20, в следует, что рабочая зона, соответствующая работе насосов при высоких КПД, сужается.
характеристики напора и мощности становятся все более крутопадающими, а из рисунка 3.20, в следует, что рабочая зона, соответствующая работе насосов при высоких КПД, сужается.
Коэффициент быстроходности характеризует всегда одно рабочее колесо, поэтому ns в многоступенчатых насосах определяется для одной ступени (весь напор насоса делится на число ступеней). В случае, если насос имеет колесо с двухсторонним подводом жидкости, это равносильно двум параллельно работающим колесам, поэтому при подсчете коэффициента быстроходности подача берется вдвое меньше (Q/2).
Дата добавления: 2016-01-07; просмотров: 837;
