Кинетическая энергия системы материальных точек.

Мера движения материальной точки, называемая кинетической энергией, определяется формулой:

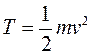
в которой через т и v обозначены соответственно масса и вели­чина скорости рассматриваемой точки. Кинетической энергией системы материальных точек назы­вается сумма кинетических энергий всех входящих в систему точек:

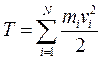(3.84)

Кинетическая энергия согласно этому определению является существенно положительной величиной, обращающейся в нуль лишь в том случае, когда скорости всех входящих в систему точек обра­щаются в нуль, т. е. в случае покоя системы. Технической единицей кинетической энергии является, как и единица работы, 1 кГм. В физической системе единицей кинетической энергии является

1 эрг= 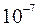джоуля. При вычислении кинетической энергии оказывается полезным прием разложения движения системы на поступательное движение ее вместе с центром инерции и относительное движение вокруг центра инерции. Докажем следующую теорему:

кинетическая энергия системы материальных точек равна сумме кинетической энергии всей массы системы, мысленно сосре­доточенной в ее центре инерции и движущейся со скоростью центра инерции, и кинетической энергии системы в ее относи­тельном движении по отношению к поступательно движущейся системе отсчета с началом в центре инерции:

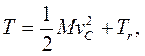(3.85)

Эта теорема была дана голландским математиком С. Кенигом, жившим в первой половине XVIII столетия. В формуле (3.85) через М обозначена масса всей системы, через 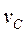- скорость центра инерции ее; кинетическая энергия си­стемы в ее относительном движении равна

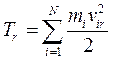
где 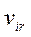- величина скорости массы 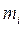, по отношению к системе, поступательно движущейся с центром инерции. Отбросим сначала предположение, что начало О поступательно движущейся системы Ox'y'z' взято в центре инерции движущейся системы материальных точек. Абсолютную скорость 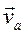точки системы представим как геоме­трическую сумму ее относительной скорости в системе Ox'y'z' и переносной скорости

,

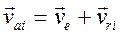При посту­пательном движении системы скорости всех ее точек одинаковы; поэтому, обозначая через v₀ скорость начала О этой системы, имеем:

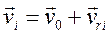
Подстановка этого выражения в (111) дает:

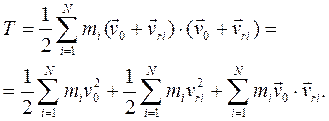
Обозначив 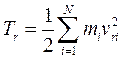(кинетическая энергия точек в относительном движении) и 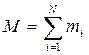, получим:

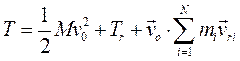(3.86)

Преобразуем выражение суммы, стоящей в третьем слагаемом этой формулы. Для этого вспомним, что

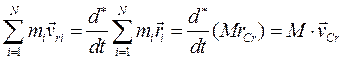
где 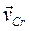представляет скорость центра инерции по отношению к движущейся системе Ox'y'z'. Указанная подстановка в (3.86) при­водит теперь к соотношению

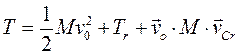(3.87)

Это представление выражения кинетической энергии в ряде слу­чаев может оказаться полезным, но чаще всего следует предпочесть принять за начало отсчета подвижной системы осей центр инерции движущейся системы; тогда 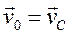, 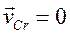(скорость центра масс относительно центра масс естественно равна нулю) и получаем теорему в вышеприведённой формулировке

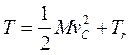(3.88)

Отметим, что в (3.87) через 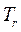обозначена кинетическая энергия системы в ее движении относительно поступательно движущейся системы Ox'y'z' с началом в точке О, а в (3.88) — такая же величина, но при условии, что началом системы отсчета является центр инерции.