Особенности растровой графики
Растровая графика представляет изображения в виде массива (матрицы) цифр. Поэтому при большом увеличении все точечные изображения выглядят как мозаика (сетка), состоящая из мельчайших ячеек. Сама сетка получила название растровой карты (bitmap), а ее единичный элемент (как уже отмечалось ранее) называется пикселем. Поскольку пиксели малы, то границы между ними незаметны и глаз воспринимает пиксельную мозаику как одно целое изображение. Тем не менее, при увеличении растрового изображения (и это один из недостатков растровой графики) точечная структура растрового изображения становится очевидной. Дело в том, что при масштабировании растровых изображений возникают характерные ступенчатые искажения (aliasing). В большинстве растровых редакторов эту лесенку удается частично убрать за счет специальных приемов (anti-aliasing), но качество картинки от этого заметно снижается. Этот эффект особенно сильно проявляется при использовании растровых шрифтов (расширение FON), которые, в отличие от векторных (с расширением TTF) при увеличении становятся нечеткими (рис. 1.5).
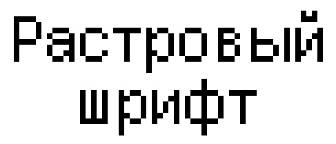
Рис. 1.5. Aliasing растрового шрифта при его масштабировании
Говоря о достоинствах и недостатках растровой графики, следует заметить следующее. По своей сути все окружающие нас объекты человек видит на растровой основе: вряд ли кто воспринимает утренний туман над рекой как набор математических формул (векторов). Поэтому одним из достоинств растровой графики является простота ее понимания, восприятия человеком, а также простота оцифровки подобной информации аппаратными средствами - сканером, цифровой фотокамерой, монитором, принтером.
Однако растровые графические файлы очень объемны и тяжелы: как только вы попытаетесь отсканировать любую фотографию с максимальными разрешением и глубиной цвета, тут же эта картинка потребует для своего сохранения целый лазерный диск. Другой недостаток: при попытке повернуть растровый рисунок на некоторый угол четкие линии превращаются в ступеньки. То есть любые трансформации (повороты, масштабирование, наклоны) в точечной графике не бывают без искажений. То же относится и к тексту.
Дата добавления: 2016-01-07; просмотров: 862;
