Селекция (отбор) отметки в стробе для продолжения траектории
В процессе слежения за траекторией в стробы автосопровождения кроме истинных будут попадать также ложные отметки, образованные нескомпенсированными в приёмном устройстве и УПО остатками помех. На рис. показан двухмерный строб сопровождения, границы которого определены на n-ный обзор по результатам сопровождения в (n-1) предыдущих обзорах.
Центр строба, помеченный треугольником, соответствует ожидаемым (экстраполированным) координатам сопровождаемой цели Xэn, Yэn в n-ом обзоре. Точками отмечены измеренные координаты истинной и ложных отметок, поступивших в n-ом обзоре из УПО в пределах границ строба. В результате анализа ситуации в стробе возможны следующие решения:
1. При наличии в стробе нескольких отметок продолжать траектории по каждой из них, т. е. допускать размножение траекторий. Продолженные по ложным отметкам траектории из-за отсутствия подтверждений через несколько обзоров будут сброшены с сопровождения, а продолженная по истинной отметке траектория останется. Такой способ обработки новых отметок чрезвычайно трудоёмок. Более того, при высокой плотности ложных отметок возможно лавинообразное размножение ложных траекторий, приводящее к перегрузке запоминающих устройств вычислительных средств.
2. Выбрать в стробе одну отметку, вероятность принадлежности которой к сопровождаемой траектории наибольшая, а остальные отбросить как ложные. Такой подход целесообразен с точки зрения уменьшения трудоёмкости вычислений, но требует решения задачи оптимальной селекции истинной отметки.
| Хэn, Yэn |
| DYn стр |
| DХn стр |
| Рис.12.2 Строб сопровождения, истинная и ложные отметки в n-ом обзоре |
Основное статистическое отличие отклонений истинной отметки и ложной от центра строба заключается в том, что закон распределения вероятностей отклонения истинной отметки носит нормальный характер, а ложной отметки - равномерный. В этих условиях естественным упрощением оптимальной операции по критерию максимального правдоподобия является селекция по минимуму суммы квадратов линейных отклонений от центра строба. Если предположить, что селекция производится в сферической системе координат в стробе, то критерий отбора отметки
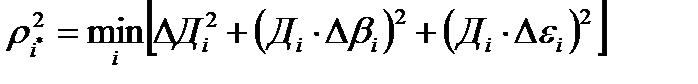 (1)
(1)
где i* - номер отметки, принятой за истинную (i=1,2...m; m - число отметок в стробе);
DДi, Dbi, Dei - отклонения i-ой отметки от центра строба, т.е. от экстраполированной точки.
При сопровождении одиночной цели в прямоугольной системе координат по данным двухкоординатной РЛС критерий отбора отметки выглядит аналогично
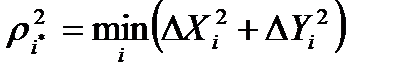 (2)
(2)
Качество процесса селекции отметок можно оценить вероятностью правильной селекции, т. е. вероятностью события, состоящего в том, что в очередном обзоре для продолжения траектории будет отобрана истинная отметка. Если попадание в строб ложных отметок обусловлено только влиянием помех и эти отметки распределены в двумерном прямоугольном стробе равномерно, то вероятность правильной селекции вычисляется по формуле
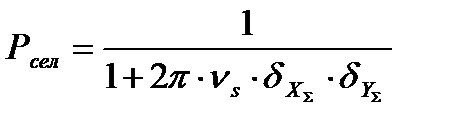 , (3)
, (3)
где 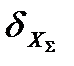 ,
, 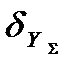 - среднеквадратические значения отклонения истинной отметки от центра строба, вызванного ошибками дискретных измерений координат и ошибками вычисления экстраполированных на данный обзор координат цели;
- среднеквадратические значения отклонения истинной отметки от центра строба, вызванного ошибками дискретных измерений координат и ошибками вычисления экстраполированных на данный обзор координат цели;
ns - плотность ложных отметок на единицу площади строба S=DXстр×DYстр, зависящая от вероятности ложного обнаружения Pло и числа разрешаемых элементов M в пределах строба автосопровождения
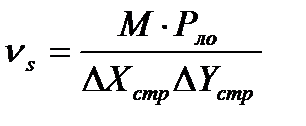 (4)
(4)
Для случая селекции в трёхмерном стробе вероятность правильной селекции рассчитывается по приближённой формуле
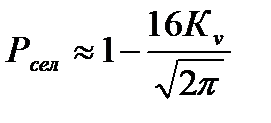 (5)
(5)
где 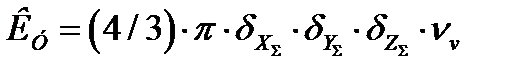 ;
;
nv - плотность ложных отметок на единицу объёма строба.
На рисунке приведена структурно-логическая схема алгоритма селекции (отбора) отметки в двумерном стробе по минимальному отклонению от его центра в прямоугольной системе координат (блоки, не относящиеся к алгоритму селекции, показаны на рисунке штриховой линией).
Под отметками, поступающими из УПО на вход блока 2, будем понимать формуляр, т.е. совокупность двоичных кодов, включающую измеренные координаты (дальность, пеленг) отметки и некоторые дополнительные признаки пачки импульсов, выявленные в процессе её первичной обработки. Последовательность операций этого алгоритма следующая:
1. По результатам обработки координат отметки в предыдущем, (n-1)-ом обзоре вычисляются координаты центра и размеры строба автосопровождения на следующий, n-ый обзор (блок 1), т. е. производится математическое стробирование. При выборе размеров строба учитываются признаки, содержащие информацию о пропусках отметок на предыдущих обзорах, о манёвре цели и др. Форма и размеры строба выбираются так, чтобы вероятность попадания истинной отметки в очередном n-ом обзоре была не меньше заданной.
2. Из общего числа отметок, поступивших из УПО в УВО в n-ом обзоре (блок 2), отбираются отметки, попавшие в строб, т. е. удовлетворяющие условию
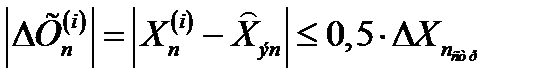
(6)
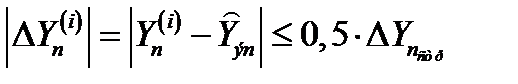
и подсчитывается их число. В этих неравенствах 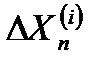 ,
, 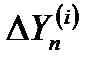 - отклонение измеренных координат i-ой отметки в n-ом обзоре
- отклонение измеренных координат i-ой отметки в n-ом обзоре 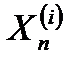 ,
, 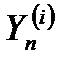 от предварительно вычисленных экстраполированных координат цели
от предварительно вычисленных экстраполированных координат цели 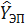 ,
, 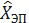 , принимаемых в качестве центра строба.
, принимаемых в качестве центра строба.
| Рис.12.3 Структурно-логическая схема селекции |
| Расчет размеров строба |
| Отбор отметок в стробе |
Вычисление 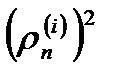
|
Отбор отметки 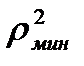
|
| Проверка критерия сброса |
| Выдача ЭО в качестве измеренной |
| Фильтрация и экстраполяция параметров |
| m=0 |
| m=1 |
| Признаки |
| Отметки |
| m>1 |
| Сброс |
| Нет |
Если в n-ом обзоре в строб сопровождаемой цели попала только одна отметка (m=1), что она считается истинной и сразу подаётся на вход блока фильтрации и экстраполяции параметров траектории, где используется для оценки координат цели в n-ом обзоре. Эта оценка используется при последующих операциях для вычисления текущих координат цели, а также для вычисления экстраполированных координат цели в (n+1)-ом обзоре, которые в блоке 1 используются в качестве центра строба.
Если в стробе обнаружено несколько отметок (m>1), то все они поступают в блок 3, где вычисляются квадраты расстояний каждой отметки от центра строба
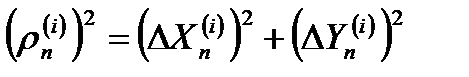 (7)
(7)
3. Сравниваются квадраты расстояний (блок 4) и выбирается одна отметка для которой
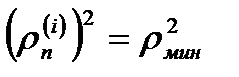 (8)
(8)
4. Если в стробе не обнаружено ни одной отметки (m=0), то проверяется критерий сброса траектории с сопровождения (блок 7). При выполнении критерия сброса траектория снимается с сопровождения. Если же критерий сброса не выполняется, то выдаётся команда на продолжение траектории путём экстраполяции её координат (блок 6).
Кроме отклонений от центра строба для селекции отметок могут быть использованы признаки "веса" отметок, которые формируются в процессе первичной обработки как некоторый аналог отношения сигнал/помеха. В простейшем случае обработки двоично-квантовых сигналов для формирования признака "веса" отметки можно использовать число импульсов в пачке.
Признаки "веса" отметок могут использоваться в процессе селекции совместно с признаком отклонения от центра строба или самостоятельно.
Один из возможных вариантов совместного использования признаков "веса" и отклонения отметок от центра строба состоит в следующем. Все отметки, попавшие в строб, разделяются на отметки с "весом" P1 и отметки с "весом" P0 в зависимости от того, превышает или нет ширина пачки некоторое пороговое значение, зависящее от удаления цели. При наличии нескольких отметок с "весом" P1 в качестве истинной принимается ближайшая к центру строба отметка этой группы. При отсутствии отметок с "весом" P1 выбирается ближайшая к центру строба отметка с "весом" P0. Если характеризовать "веса" отметок непосредственно числом импульсов в пачке, что можно селектировать отметку по максимальному числу импульсов в пачке. Признаки отклонения отметок от центра строба используются в этом случае только при равенстве "весов" нескольких отметок.
Селекция отметок методом "вытеснения"
Наряду с методом отбора отметок по минимальному отклонению от центра строба находит применение метод "вытеснения" отметок в пределах строба с переменными границами по двум координатам. Сущность этого метода заключается в том, что при попадании очередной отметки в прямоугольный строб он заменяется стробом, подобным старому, с центром подобия в экстраполированной точке.
Новый строб строится таким образом, чтобы вновь поступившая из УПО отметка находилась на одной из его границ.
Вначале с целью упрощения предположим, что строб автосопровождения имеет квадратную форму и допустим, что координаты первой из отметок, поступивших в n-ом обзоре  ,
, 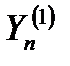 таковы, что
таковы, что 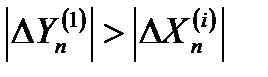 .
.
Тогда после поступления этой отметки каждая сторона строба уменьшается до величины 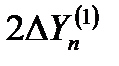 . При поступлении последующих отметок (например,
. При поступлении последующих отметок (например, 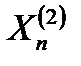 ,
, 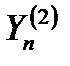 ) с отклонениями от центра строба
) с отклонениями от центра строба 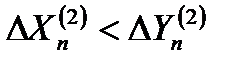 или
или 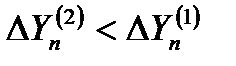 размеры строба будут постепенно уменьшаться, "вытесняя" отметки за пределы уменьшающегося строба. Последняя из попавших в строб отметок и используется для продолжения траектории.
размеры строба будут постепенно уменьшаться, "вытесняя" отметки за пределы уменьшающегося строба. Последняя из попавших в строб отметок и используется для продолжения траектории.
| Рис.12.4 Селекция отметок в стробе методом "вытеснения" |
| DYn стр |
| DХn стр |
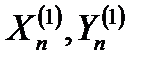
|
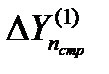 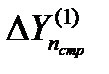
|
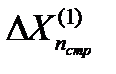
|
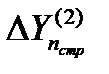
|
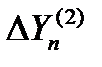
|
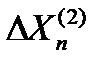
|
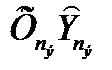
|
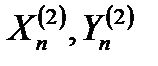
|
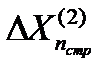
|
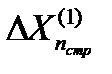
|
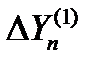
|
Подобие формы последовательно уменьшающегося строба обеспечивается следующим образом. Если очередная отметка с координатами (Д (i), П (i)) располагается относительно экстраполированной точки (Дэ, Пэ) так, что выполняется неравенство
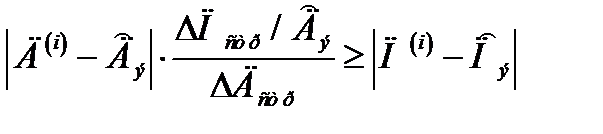 , (9)
, (9)
то это означает, что отклонение отметки по дальности больше её линейного отклонения по пеленгу. В этом случае через отметку (Д(i), П(i)) должна проходить новая граница строба по дальности. Тогда подобный строб имеет ширину 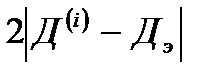 по дальности и
по дальности и 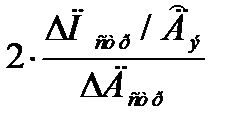 по пеленгу.
по пеленгу.
Если же новая отметка располагается так, что её линейное отклонение от центра строба по пеленгу больше, чем отклонение по дальности, т. е. если выполняется условие
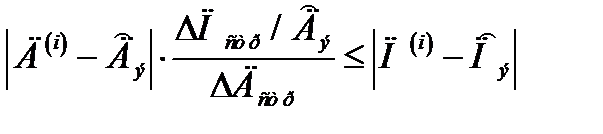 , (10)
, (10)
то через неё проходит граница нового строба по пеленгу. При этом ширина строба по пеленгу определяется величиной 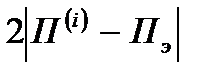 , а по дальности
, а по дальности
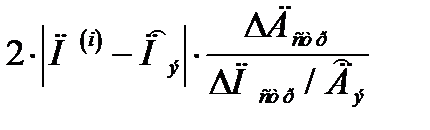 (11)
(11)
Таким образом, и при автосопровождении цели в полярной системе координат из всех попавших в первоначальный строб отметок выбирается та, которая находится на границе минимального строба, подобного исходному.
ВТОРОЙ УЧЕБНЫЙ ВОПРОС: Отбор отметок в перекрывающихся стробах. Физическое стробирование.
Дата добавления: 2016-01-07; просмотров: 1621;
