Эксцентриковые механизмы

Рассмотрим эксцентриковые зажимы. Эксцентрик представляет собой соединение в одной детали двух элементов – круглого диска радиуса r (Рисунок 2.39 – Эксцентрик) и плоского односкосого клина. При повороте эксцентрика вокруг оси вращения диска 0 клин входит в зазор между диском и заготовкой и развивает силу зажима Q.

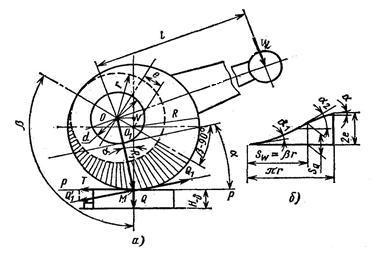
Рисунок 2.39 – Эксцентрик

Рабочая поверхность эксцентриков может быть окружностью (круговые) или спиралью (криволинейные). Различие их заключается в том, что в развертке круговых эксцентриков плоский клин получается криволинейным с переменным углом α в зависимости от угла поворота β (Рисунок 2.39, б – Эксцентрик), а у криволинейных эксцентриков α не зависит от β. Это означает, что криволинейные эксцентрики создают стабильную силу зажима в партии заготовок, а круговые – нет. При зажиме круговыми эксцентриками в зависимости от колебания размера Н_Тн в партии заготовок изменяется рабочий угол поворота β, а следовательно, угол α и сила зажима Q. В то же время технология изготовления круговых эксцентриков значительно проще, чем криволинейных. Поэтому широко распространены круговые эксцентрики с углом β=30÷135° для уменьшения колебаний Q₁ в партии.

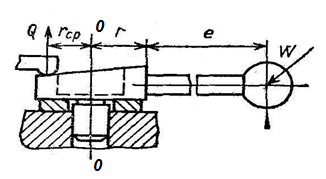
Рисунок 2.40 - Схема зажимного механизма с торцовым кулачком

Эксцентриковые зажимы являются самыми быстродействующими из всех ручных зажимных механизмов. По быстродействию они сравнимы с пневмозажимами.

Недостатками эксцентриковых зажимов являются: малая величина рабочего хода, ограниченная величиной рабочего хода, ограниченная величиной эксцентриситета; повышенная утомляемость рабочего, так как при откреплении заготовки рабочему необходимо прикладывать силу, обусловленную свойством самоторможения эксцентрика; ненадежность зажима при работе инструмента с ударами или вибрациями из-за опасности самооткрепления.

Несмотря на эти недостатки, эксцентриковые зажимы широко используют в приспособлениях, особенно для мелкосерийного и серийного производств.

При проектировании эксцентрикового зажима необходимо по требуемой для закрепления заготовки силе зажима Q определить его конструктивно-размерные параметры. Исходными данными для расчета являются: Тн – допуск на размер Н заготовки от базы до точки приложения силы зажима; β – рабочий угол поворота эксцентрика от нулевого (начального) положения; Q – требуемая для закрепления заготовки сила. Результатом расчета должны быть: е – эксцентриситет эксцентрика, d – диаметр цапфы, R – радиус рабочей поверхности эксцентрика, В – ширина рабочей поверхности, l – длина рукоятки (при ручном зажиме).

Если угол β поворота эксцентрика не ограничен, то эксцентриситет е определяют из условия 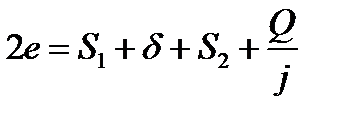, где S₁ – минимальный зазор, обеспечивающий свободную установку заготовки c максимальным размером Н; S₂ – запас хода эксцентрика, предохраняющий его от перехода через мертвую точку; j – жесткость узла зажима. Отношение Q/j учитывает увеличение расстояния между заготовкой и эксцентриком за счет упругой деформации деталей узла зажима, воспринимающих силу Q.

При угле β < 180º величину е можно определить из уравнения перемещений эксцентрика. Это уравнение можно записать из схемы на рисунке 2.40 - Схема зажимного механизма с торцовым кулачком

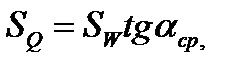(2.96)

приняв 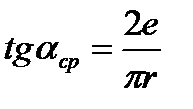и записав 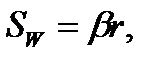получим

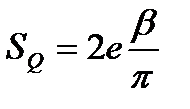. (2.97)

С другой стороны, необходимая величина рабочего хода определяется условием

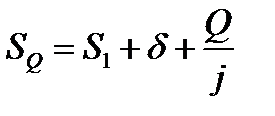
тогда,

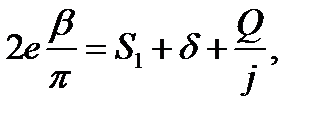
откуда

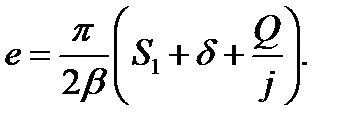(2.98)

Диаметр цапфы эксцентрика d можно определить из условия отсутствия контактных деформаций смятия, задаваясь ее шириной b:

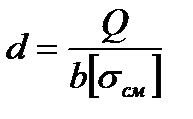(2.99)

где: [σ_см] – допускаемое напряжение на смятие материала цапфы.

Радиус рабочей поверхности эксцентрика R определяют из условия самоторможения эксцентрика. Для этого необходимо, чтобы угол подъема криволинейного клина α был меньше угла самоторможения α_с. Это условие можно записать из схемы на рисунке 2.38, а - Схемы одноплунжерных зажимных механизмов. На схеме действие эксцентрика на заготовку условно заменено действием плоского односкосого клина с углом α в зазоре между заготовкой и цапфой эксцентрика. Точка касания наклонной плоскости и цапфы лежит на радиусе R₁, соединяющем ось вращения эксцентрика 0 с точкой М приложения зажимной силы. Тогда

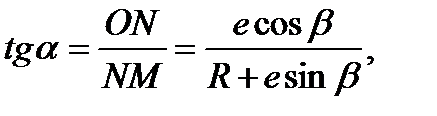
откуда

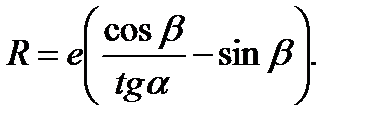(2.100)

Приняв в формуле (2.100) α = α_с, можно рассчитать величину R, обеспечивающую самоторможение эксцентрика.

Ширину рабочей части эксцентрика В (на рисунке 2.39 Эксцентрик не показана) определяют из уравнения напряжений смятия в месте контакта его с заготовкой или промежуточной деталью

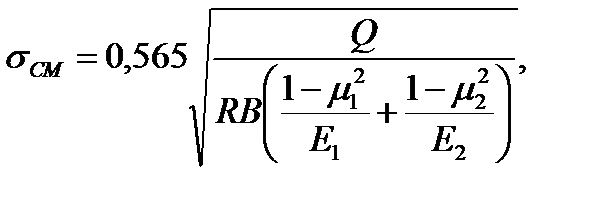(2.101)

где: 0,565 – коэффициент; E₁, Е₂, μ₁ μ₂ – модули упругости и коэффициенты Пуассона, соответственно, для материалов эксцентрика и заготовки или промежуточной детали.

Чаще всего между эксцентриком и заготовкой помещают промежуточную деталь (или эксцентрик соединяют с другим простым механизмом, например с рычажным), изготовленную из одинакового с эксцентриком материала. Изготовлять эксцентрики рекомендуется из стали 20Х с цементацией рабочей поверхности на глубину 0,8-1,2 мм и закалкой до твердости HRC 55-60 (ГОСТ 9061-68). Приняв Е₁ = Е₂ и μ₁ =μ₂=0,25 (для стали), получим

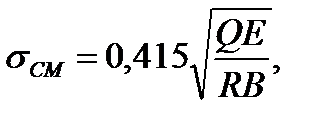
откуда

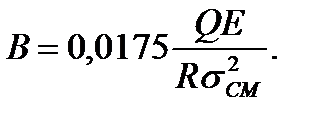(2.102)

Уравнение сил в круговом эксцентрике с достаточной для практических расчетов точностью можно записать, заменив действие эксцентрика действием плоского односкосого клина с углом α в зазоре между цапфой и поверхностью заготовки. Схема такой замены и сил, действующих на эксцентрик и фиктивный клин, приведена на рисунке 2.37 – схема механизма с плоским клином и силы, действующие на клин. На схеме Q_l – сила, действующая. на плоскость зажима рр, под углом α. Вдоль плоскости действует сила T=Q′₁ cos α. Эту силу можно рассматривать как внешнюю, действующую на клин с углом α. Тогда, используя формулу (2.102)

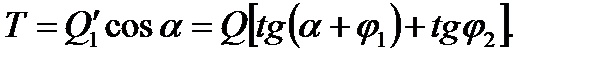(2.103)

Из условия равновесия эксцентрика получим 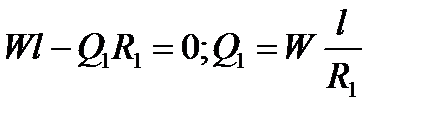, так как 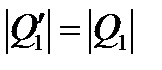. Подставив значение Q₁ в формулу (2.103) и опустив cos α как величину, близкую к единице при малых углах α, получим

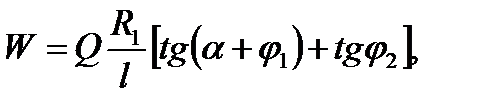(2.104)

Усилие развиваемое эксцентриком:

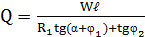(2.105)

где: R₁, α – переменные величины. Для пользования этой формулой необходимо уметь определять угол α и радиус R₁ в зависимости от угла поворота β. Из прямоугольного треугольника MNO (Рисунок 2.39 - Эксцентрик)

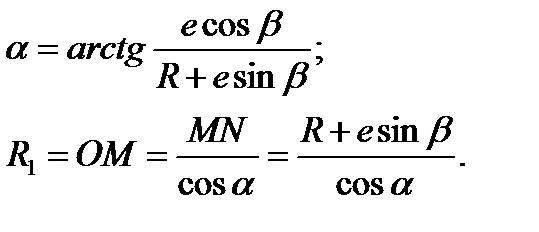(2.106)

При проектировании ручных эксцентриковых зажимов задаются силой W на рукоятке и из уравнения (2.105) определяют длину рукоятки

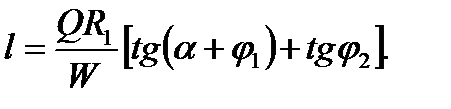(2.107)

Торцевой кулачок

Торцевой кулачок является разновидностью клинового механизма, у которого плоский односкосный клин укреплен на цилиндре радиуса r. Для создания силы зажима Q кулачок должен вращаться вокруг оси ОО этого цилиндра силой W, приложенной на рукоятке длиной l (Рисунок 2.40 – Схема зажимного механизма с торцовым кулачком). Силу W можно определить по формуле

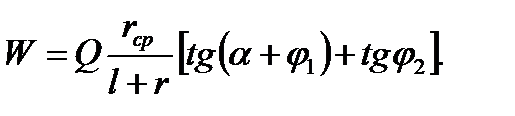(2.108)

Рычажные механизмы

Рычажные зажимы используют в виде двуплечего рычага в сочетании с различными силовыми источниками. При помощи рычага можно изменять величину и направление силы зажима, а также осуществить одновременное закрепление заготовки в двух местах.

Конструктивных разновидностей рычажных зажимов много, однако все они сводятся к трем силовым схемам, приведенным на рисунке 2.41, а - силовые схемы рычажных механизмов, где приведены также формулы расчета Q идеальных механизмов (без учета сил трения с учетом равенства плеч ℓ₁ и ℓ₂.

В первом случае 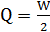, во втором Q=W, в третьем Q=3W.

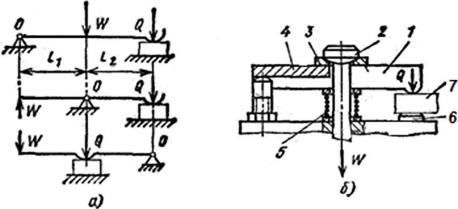
Рисунок 2.41 - Силовые схемы рычажных зажимов

Рассмотрим пример расчета силы зажима рычагом с учетом сил трения. Схема сил, действующих на рычаг, приведена на рисунке 2.42 – Схема сил, действующих в рычажном зажиме. При закреплении рычагом возникают силы трения F₁ и F₂ на поверхностях контакта рычага со штоком привода и заготовкой. В цапфе рычага возникает реакция S, создающая на плече ρ = rf момент трения (ρ – радиус круга трения).

Угол φ_ср отклонения силы S с достаточной точностью можно принять равным среднему значению между. φ₁ и φ₂:

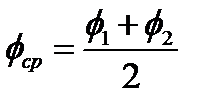(2.109)

Силу S можно принять равной сумме сил Т₁ и Т₂:

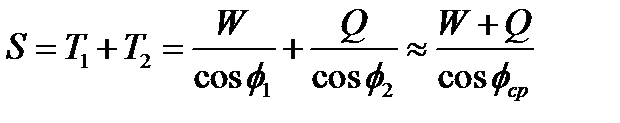(2.110)

Из условия равновесия рычага имеем

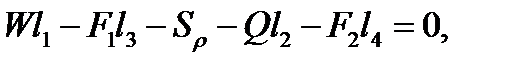
где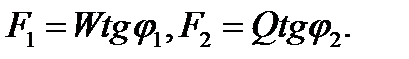

Тогда, учитывая формулы для определения F₁ , F₂, S,

.

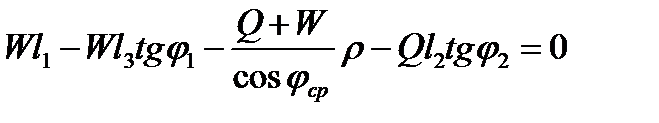Откуда

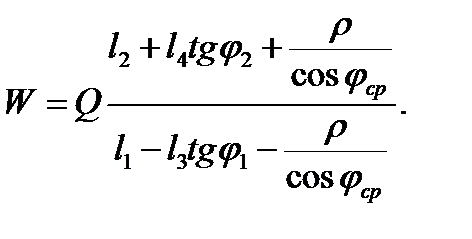(2.111)

Потери на трение в рычажном зажиме составляют 1,5-6%.

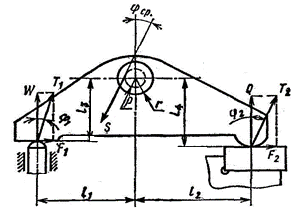
Рисунок 2.42 - Схема сил, действующих в рычажном зажиме

Анализ схем (Рисунок 2.41, а - Силовые схемы рычажных зажимов) показывает, что наибольший выигрыш в силе (наибольшее передаточное отношение) дает третья схема, однако в конструктивном отношении она громоздка, а в эксплуатации неудобна, так как требует большого рабочего, хода силового источника и усложняет загрузку заготовки под рычаг. Вторая схема применяется в тех случаях, когда требуется изменить направление исходной силы. Первая схема дает наиболее компактную конструкцию, однако передаточное отношение сил в ней всегда меньше единицы.

На рисунке 2.41, б - Силовые схемы рычажных зажимов, приведен пример конструктивного оформления рычажного зажима по первой схеме. Рычаг 1 при зажиме заготовки 7, установленной на опоры 6, поворачивается относительно упора 4. Сила от источника на рычаг передается через тягу 2 и сферическую шайбу 3. Сферическая шайба 3 предохраняет тягу 2 от внецентренного приложения нагрузки. Пружина 5 обеспечивает обратный ход рычага при откреплении заготовки.