ИЗУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

Из уравнений Максвелла следует, что электромагнитное поле в пространстве может существовать в виде волн. В работе изучается частный случай электромагнитной волны - монохроматическая волна, в которой векторы напряженности электрического и магнитных полей 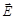и и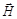зменяются в пространстве и во времени по гармоническому закону

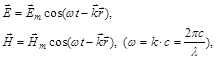
где 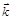- волновой вектор; с - скорость света в вакууме. При этом вектор 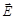всегда перпендикулярен вектору 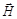и каждый из них перпендикулярен направлению распространения волны, которое определяется волновым вектором .

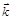Для волн УКВ-диапазона (ультракоротких радиоволн волн 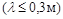, изучаемых в работе, характерна плоская (линейная) поляризация: колебания вектора 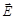происходят только в одной плоскости, определяемой векторам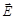и и .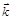

Интенсивность I электромагнитной волны в вакууме пропорцио-нальна квадрату амплитуды напряжённости электрического поля: 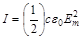, так что измеряя квадрат амплитуды напряжённости электрического поля, можно с точностью до коэффициента определить интенсивность такой волны.

В качестве приёмника электромагнитной волны в работе исполь-зуется диодный (кристаллический) высокочастотный детектор, имею-щий приблизительно квадратичную зависимость тока от напряжения на начальном участке вольт-амперной характеристики (i ~ U²). Поэтому ток, проходящий через диод, пропорционален интенсивности электромагнитной волны ( 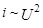, a U_д~E_m, т.е. i~ 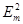~I). Помимо этого, такой приёмник обладает избирательностью по направлению колебаний электрического поля, что позволяет изучать свойства поляризации электромагнитной волны. Например, плоскополяризованная электромагнитная волна подчиняется закону Малюса: интенсивность волны, измеренная детектором в плоскости, составляющей угол a с плоскостью колебаний вектора Е, определяется как

I = I₀ cos²a,

где I₀ - интенсивность бегущей волны.

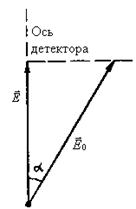Рисунок 1

Закон Малюса легко объяснить, если учесть, что детектор реагирует только на проекцию вектора 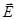на ось самого детектора. Пусть Е₀ - амплитуда напряжённости электрического поля падающей волны, тогда детектор будет воспринимать только составляющую с амплитудой E_m = E₀cosa (рисунок 1). Измеряемая детектором интенсивность I~ 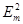, отсюда и следует закон (1).

Если на пути плоской электромагнит-ной волны поставить отражающую поверх-ность, можно получить стоячую волну с рас-пределением узлов (или пучностей) в прост-ранстве через a/2 для каждого из колеблю-щихся векторов 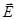и :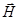

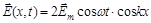
(для стоячей волны между векторам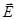и и 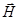как во времени, так и в пространстве наблюдается сдвиг фаз на a/2). Измеряя распределение узлов (или пучностей) напряжённости электрического поля стоячей электромагнитной волны вдоль направления распространения, можно определить длину волны.

4. ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ

1. Рупорный излучатель.

2. Кристаллический детектор.

3. Вольтметр.

4. Оптическая скамья.

5. Отражатель.

5. ОПИСАНИЕ УСТАНОВКИ

Установка (рисунок 2) состоит из генератора электромагнитных колебаний 1 с рупорным излучателем, металлического отражателя 6, детектора 2, милливольтметра и источника питания.

Напряжение U на нагрузочном сопротивлении детектора, пропор-циональное току i детектора, измеряется милливольтметром. Детектор 2 укреплён на конце держателя 3, сделанного из пенопласта (диэлектрическая проницаемость пенопласта близка к диэлектрической проницаемости воздуха, поэтому зонд из пенопласта практически не искажает картину поля).

Держатель 3 может вращаться вокруг своей горизонтальной оси. Шкала 4 служит для отсчёта углов поворота детектора.

Кронштейн с детекторами и отсчётным устройством можно посту-пательно перемещать вдоль направляющей 5. Перемещение измеряют по линейке на направляющей.

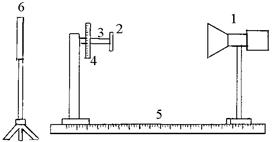Рисунок 2

6. ВЫПОЛНЕНИЕ РАБОТЫ

1. Определение длины электромагнитной волны

Установите металлический отражатель 6 (рисунок 2) напротив излучателя 1. Включите питание генератора и милливольтметра. Вращая детектор вокруг горизонтальной оси, найдите положение, при котором показания милливольтметра максимальны (положение детектора не должно совпадать с узлом электромагнитной волны). Добейтесь перпендикулярности расположения отражателя к направлению распространения волны: показания милливольтметра в узле должны быть близкими к нулю, а в пучности - наибольшими.

Снимите зависимость напряжения U детектора от его координаты x. Проведите не менее десяти измерений через 2...3 мм, особенно тща-тельно фиксируя положения пучностей и узлов. Постройте график зависимости U(x) и по нему определите a.

2. Проверка закона Малюса

Уберите отражатель. Установите детектор против излучателя (рисунок 2) на расстоянии l 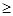70 см от последнего. Вращая детектор вокруг горизонтальной оси, снимите зависимость напряжения U детектора от угла поворота a (по лимбу 4). Снимите 20...25 показаний через 5⁰, фиксируя угловые положения максимумов и минимумов интенсивности волны. Постройте график U(a) и сравните с теоретической зависимостью I(a), нормируя теоретическую кривую по максимуму экспериментальной кривой.

3. Исследование зависимости интенсивности волны от расстояния

Приёмный детектор установите по максимуму показания милли-вольтметра. Перемещая излучатель 1, снимите зависимость напряжения U от расстояния x между излучателем и детектором. Измерения проведите в интервале значений x от 40 до 80 см через каждые 5 см.

Постройте график зависимости lgU отlgx. Вычислите тангенс угла наклона графика (для сферической волны U~x^-2, и тангенс угла наклона графика должен быть равным двум). Сделайте вывод о характере излучаемой волны.