Основные определения. Все электрические цепи являются нелинейными

Все электрические цепи являются нелинейными. Они могут считаться линейными в ограниченных диапазонах значений токов и напряжений. Например, при чрезмерно больших токах происходит значительный нагрев материала проводников, сопровождающийся резкими изменениями их сопротивлений.
В линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения. Вольтамперные характеристики линейных элементов (зависимость напряжения на элементе от тока) являются прямыми линиями (рис. 5.1).

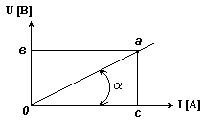
Рис. 5.1

Электрическое сопротивление линейного элемента пропорционально тангенсу угла наклона его вольтамперной характеристики к оси тока.

,

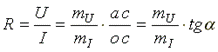где mU и mI - масштабы напряжения и тока.

В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения.
Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат.
Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока.
Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики (рис. 5.2), а полупроводниковые диоды - несимметричные характеристики (рис. 5.3).

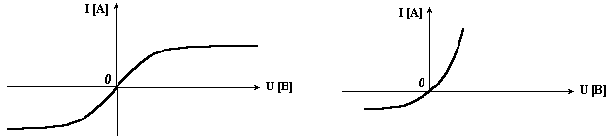
Рис. 5.2 Рис. 5.3

Статическим или интегральным сопротивлением нелинейного элемента называется отношение напряжения на элементе к величине тока. Это сопротивление пропорционально тангенсу угла наклона α между осью тока и прямой, проведенной из начала координат в точку а характеристики.

.

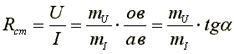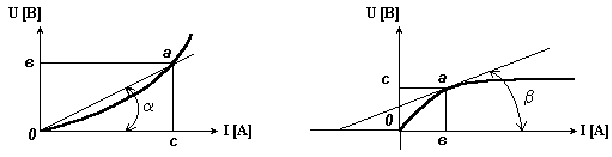
Рис. 5.4 Рис. 5.5

Дифференциальное, или динамическое, сопротивление нелинейного элемента - это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока.

Это сопротивление пропорционально тангенсу угла наклона β между осью тока и касательной к точке a характеристики.

.

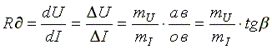При переходе от одной точки вольтамперной характеристики к соседней статическое и динамическое сопротивления нелинейного элемента меняются.
Статическое и динамическое сопротивления линейного элемента одинаковы и не зависят от тока или напряжения.

5.2. Графический метод расчета нелинейных цепей
постоянного тока

Известные аналитические методы непригодны для расчета нелинейных электрических цепей, так как сопротивления нелинейных элементов зависят от направления и значения тока или напряжения. Применяются графоаналитические методы, основанные на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) этих элементов. Рассмотрим электрическую цепь, состоящую из двух последовательно соединенных нелинейных сопротивлений н.с.1 и н.с.2 (рис. 5.6). ВАХ 1 и ВАХ 2 приведены на рис. 5.7.

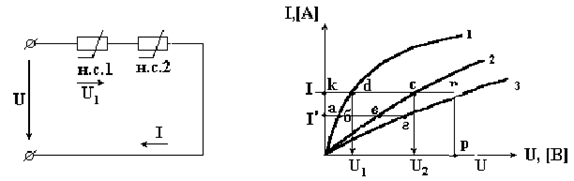
Рис. 5.6 Рис. 5.7

К цепи подведено напряжение U, и оно равно сумме падений напряжений на н.с.1 и н.с.2:

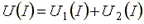(5.1)

По всей цепи протекает один и тот же ток I, так как н.с.1 и н.с.2 соединены между собой последовательно. Для определения тока в электрической цепи нужно построить результирующую ВАХ цепи. Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2 (аг = аб + ав), соответствующие одним и те же значениям тока. Далее, задаваясь произвольным значением тока (например, больше I' и меньше I' ) можно построить ВАХ всей цепи (рис. 5.7, кривая 3). Затем, пользуясь этой ВАХ, можно найти искомый ток всей цепи и искомые напряжения на н.с.1 и н.с.2. Для этого отложим на оси абсцисс отрезок 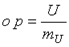(mu - масштаб напряжения источника питания) и проведем из точки p прямую, перпендикулярную оси абсцисс до пересечения с кривой 3. Получим отрезок np = ko. Ток 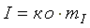(mI - масштаб тока всей цепи). Для найденного тока по ВАХ 1 и ВАХ 2 находим напряжения U1 и U2. ; .

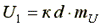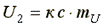При параллельном соединении двух нелинейных элементов (рис. 5.8) ток в неразветвленной части электрической цепи равен сумме токов в параллельных определенных ветвях. Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 5.9), соответствующие одним и те же значениям напряжения, так как к этим нелинейным элементам приложено одно и то же напряжение, равное напряжению внешней сети, т.е. источника питания. Например, для произвольного значения напряжения 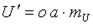находим ординату аг точки для результирующей кривой 3.
(аг = ав + аб)

Рис. 5.8 Рис. 5.9

Далее задаваясь произвольным значением напряжения больше и меньше U', можно построить ВАХ всей цепи (кривая 3). Затем, пользуясь ВАХ, можно при любом значении приложенного напряжения U (отрезок ор) найти величину общего тока I (pn = oк). Это напряжение также определяет значения токов I1 и I2 в отдельных ветвях с учетом масштаба тока mI.

В случае смешанного (рис. 5.10) соединения расчет цепи производят в следующем порядке: сначала заменяют два параллельно соединенных нелинейных элемента одним эквивалентным; схема со смешанным соединением приводится к рассмотренной ранее схеме последовательного соединения двух нелинейных элементов.

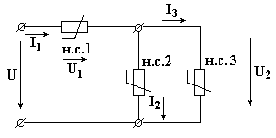
Рис. 5.10

Магнитные цепи