ВОДОСЛИВ С ШИРОКИМ ПОРОГОМ БЕЗ БОКОВОГО СЖАТИЯ
Схема прямоугольного незатопленного и без бокового сжатия водослива с горизонтальным широким порогом представлена на рис. 9.11.
На входе потока на водослив с широким порогом происходит значительное снижение свободной поверхности с образованием на этом участке кривой спада. Понижение уровня свободной поверхности связано с тем, что за счет увеличения скорости происходит повышение кинетической энергии. Это приводит к снижению потенциальной энергии, которая характеризуется уменьшением глубины потока на пороге водослива.
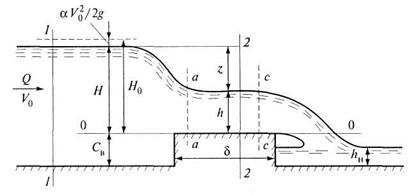
Рис. 9.11. Неподтопленный водослив с широким порогом
Примем ширину канала b по всей длине порога водослива одинаковой. Гидравлическими сопротивлениями по всей длине  водослива пренебрегаем.
водослива пренебрегаем.
Считаем, что глубина на пороге водослива h в средней его части (между сечениями а-а и с-с) постоянная. Следовательно, свободная поверхность на участке а-с горизонтальная и можно считать, что движение потока на этом участке плавно изменяющееся.
Для определения расхода через водослив используем уравнение Бернулли. За плоскость сравнения 0-0 принимаем плоскость порога водослива. Контрольные сечения: 1-1 - находится там, где не наблюдается начала определенного спада свободной поверхности в верхнем бьефе, и 2-2 - в средней части порога водослива.
Запишем уравнение Бернулли для данного случая:
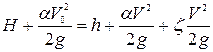 , (9.11)
, (9.11)
где Vo - средняя скорость подхода потока к водосливу; V - средняя скорость на пороге водослива в сечении 2-2; 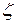 - коэффициент местных сопротивлений на входе водослива, который зависит от формы входного ребра при обтекании его потоком жидкости.
- коэффициент местных сопротивлений на входе водослива, который зависит от формы входного ребра при обтекании его потоком жидкости.
После преобразований уравнения (9.12) получим
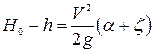 , (9.13)
, (9.13)
откуда скорость на пороге водослива
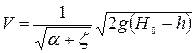 . (9.14)
. (9.14)
В этой формуле 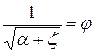 - коэффициент скорости. Коэффициент кинетической энергии
- коэффициент скорости. Коэффициент кинетической энергии 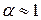 .
.
Скорость
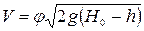 . (9.15)
. (9.15)
Расход водослива с широким порогом
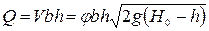 . (9.16)
. (9.16)
Расход, отнесенный к ширине потока, 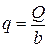 - удельный расход
- удельный расход
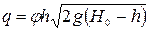 . (9.17)
. (9.17)
Принимая отношение 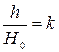 и подставляя его в формулу(9.16), расход
и подставляя его в формулу(9.16), расход
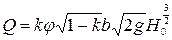 . (9.18)
. (9.18)
Выразим коэффициент расхода 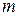 через
через 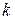 и
и 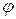 :
:
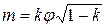 . (9.19)
. (9.19)
В результате получим следующую формулу расхода:
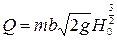 . (9.20)
. (9.20)
Выражение (9.20) аналогично основной формуле расхода водослива (9.4) без учета бокового сжатия и подтопления.
При вычислении расхода через водослив с широким порогом необходимо знать глубину на пороге водослива 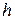 . Для определения величины
. Для определения величины 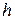 существуют разные методы, основанные на определенных теоретических предпосылках и на экспериментальных гидравлических исследованиях.
существуют разные методы, основанные на определенных теоретических предпосылках и на экспериментальных гидравлических исследованиях.
Метод Беланже
В этом методе предполагается, что при заданном напоре Н на водосливе на его пороге устанавливается глубина h, при которой расход, проходящий через водослив, будет максимальным.
Расход является функцией переменной глубины h. Следовательно, для удельного расхода (9.11) первая производная этой функции будет равна нулю:
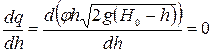 (9.21)
(9.21)
Полагая, что коэффициент скорости 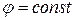 , получим
, получим
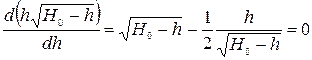 . (9.22)
. (9.22)
После преобразований (9.22) будем иметь
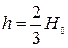 и
и 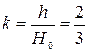 . (9.23)
. (9.23)
При глубине на пороге водослива 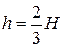 расход жидкости Q будет соответствовать
расход жидкости Q будет соответствовать 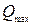 .
.
Коэффициент расхода согласно выражению (9.19)
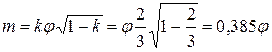 . (9.24)
. (9.24)
Зная значение коэффициента 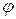 , который зависит от формы входного ребра водослива с широким порогом, можно определить коэффициент расхода
, который зависит от формы входного ребра водослива с широким порогом, можно определить коэффициент расхода 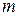 .
.
Метод Б. Бахметева
Метод заключается в том, что предполагается установление на пороге водослива глубины, равной критическому значению 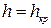 , а это соответствует тому, что удельная энергия сечения Э на пороге водослива равна минимальному его значению. При
, а это соответствует тому, что удельная энергия сечения Э на пороге водослива равна минимальному его значению. При 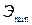 относительная глубина
относительная глубина 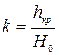 .
.
Для прямоугольного русла критическая глубина 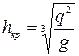 .
.
Подставив значение 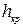 в выражение относительной глубины, получим
в выражение относительной глубины, получим
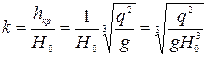 . (9.25)
. (9.25)
Преобразуем формулу удельного расхода (9.17):
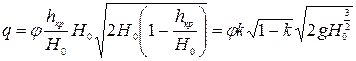 (9.26)
(9.26)
Выразив (9.25) относительно q и подставив в (9.26), получим зависимость для относительной глубины:
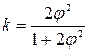 (9.27)
(9.27)
После подстановки 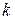 по (9.27) в формулу (9.19) коэффициент расхода m по Бахметеву
по (9.27) в формулу (9.19) коэффициент расхода m по Бахметеву
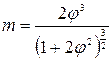 или
или 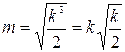 (9.28)
(9.28)
Зависимость относительной глубины 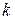 от
от 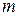 :
:
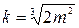 . (9.29)
. (9.29)
Метод Д. Кумина
Метод основан на результатах экспериментальных исследований водосливов с широким порогом, проведенных Д. Куминым.
В результате гидравлических исследований разными авторами водосливов с широким порогом было установлено, что теоретические предпосылки Беланже и Бахметева не совсем соответствовали результатам экспериментов по определению глубины на пороге водослива h. Экспериментально было установлено, что 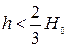 и
и 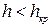 .
.
Кроме того, оказалось, что на значение коэффициента 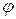 и, следовательно, коэффициента расхода
и, следовательно, коэффициента расхода 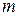 влияет высота порога водослива
влияет высота порога водослива 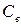 в верхнем бьефе.
в верхнем бьефе.
Расход через водослив с широким порогом определяется по формуле (9.20):
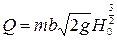 .
.
Если площадь живого сечения перед водосливом 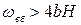 , величиной скоростного напора
, величиной скоростного напора 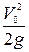 можно пренебречь и расход вычисляется по формуле
можно пренебречь и расход вычисляется по формуле
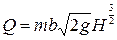 . (9.30)
. (9.30)
На основании результатов экспериментов Д. Кумин получил значения коэффициента расхода 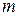 в зависимости от формы входной грани ребра водослива и относительной глубины
в зависимости от формы входной грани ребра водослива и относительной глубины 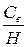 .
.
В табл. 9.1 приведены некоторые значения 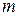 для разных видов входных граней ребра водослива.
для разных видов входных граней ребра водослива.
Таблица 9.1 Значения коэффициента т для разных входных граней ребра
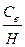
| 0,0 | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 2,0 |
| m1 | 0,385 | 0,366 | 0,356 | 0,35 | 0,345 | 0,342 | 0,333 |
| m2 | 0,385 | 0,377 | 0,374 | 0,371 | 0,367 | 0,365 | 0,362 |
| m3 | 0,385 | 0,374 | 0,365 | 0,361 | 0,358 | 0,355 | 0,35 |
Обозначения: m1 — коэффициент расхода водослива с вертикальной гранью; m2— то же с закругленной гранью; m3 — то же с притуплённой гранью под углом 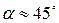 с ребром (рис. 9.12).
с ребром (рис. 9.12).
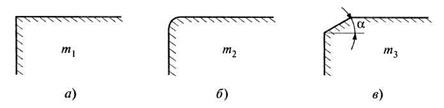
Рис. 9.12. Входные грани ребер водослива:
а - с вертикальной гранью; б - с закругленной гранью;
в - с притуплённой гранью
Значения 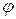 , полученные Д. Куминым, в зависимости от коэффициента расхода т приведены в табл. 9.2
, полученные Д. Куминым, в зависимости от коэффициента расхода т приведены в табл. 9.2
Таблица 9.2 Значения ф в зависимости от коэффициента расхода т
| т | 0,3 | 0,31 | 0,32 | 0,33 | 0,34 | 0,35 | 0,36 | 0,37 | 0,38 |
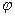
| 0,943 | 0,95 | 0,956 | 0,963 | 0,94 | 0,976 | 0,983 | 0,99 | 0,996 |
| k | 0,416 | 0,434 | 0,453 | 0,469 | 0,483 | 0,513 | 0,541 | 0,572 | 0,613 |
Значения 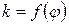 , представленные в табл. 9.2, вычислены по формуле (9.19).
, представленные в табл. 9.2, вычислены по формуле (9.19).
Зная коэффициент расхода водослива т, можно взять из табл. 9.2 значения 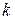 и вычислить глубину на пороге водослива
и вычислить глубину на пороге водослива 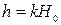 .
.
Дата добавления: 2015-12-29; просмотров: 1323;
