ВЗАИМОДЕЙСТВИЕ ТРУБЧАТЫХ КОЛОДЦЕВ

В практике водоснабжения при использовании подземных вод для водопотребления и при водопонижении применяется несколько трубчатых колодцев, располагающихся на некотором расстоянии друг от друга. Дебит отдельного колодца будет несколько меньше по сравнению с отдельно установленным колодцем.

М. Маскетом получены следующие формулы для определения притока воды к колодцу при условии, что глубина воды 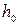во всех колодцах группы совершенных колодцев и их дебиты одинаковы.

Для двух колодцев, располагающихся на расстоянии 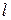друг от друга,

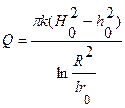. (11.57)

Глубина воды в точке С, находящейся посередине между колодцами,

. (11.58)

Для трех колодцев, размещающихся в точках вершин равностороннего треугольника со сторонами а,

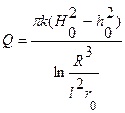. (11.59)

Глубина воды в центре треугольника

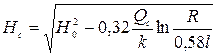. (11.60)

В случае использования четырех колодцев, находящихся в точках вершин прямоугольника со сторонам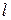и и ,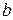

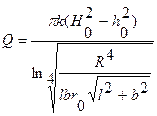. (11.61)

Глубина воды в центре прямоугольника

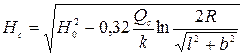, (11.62)

где 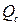- дебит группы колодцев.

Р. Форгеймером решена задача по притоку воды к трубчатым колодцам, расположенным произвольно относительно друг друга. При групповом размещении колодцев приток к одному колодцу влияет на приток к другим. Кривая депрессии каждого колодца влияет на кривые депрессии других. В результате притоков к каждому колодцу образуется общая кривая депрессии. Форгеймер предположил, что при отборе воды из группы совершенных колодцев глубина воды в некоторой точке а водоносного пласта (рис. 11.14)

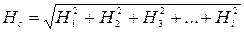, (11.63)

где H₁, H₂, H₃, ..., H_i - фиктивные глубины при отборе воды из каждого колодца, находящихся на расстоянии x₁, x₂, х₃, х₄ и x_i от точки а.

Данные фиктивные глубины соответствуют условию, что дебиты совершенных колодцев при безнапорной фильтрации не зависят друг от друга.

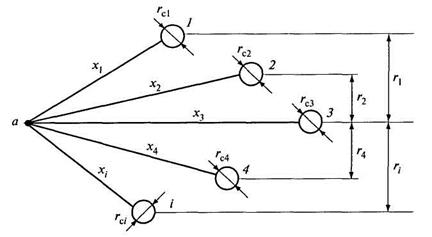
Рис. 11.14. Схема произвольного расположения совершенных колодцев

Можно считать, что точка а находится на достаточно большом расстоянии от каждого из колодцев, а расстояние между каждым из них сравнительно мало по сравнению с x₁, x₂, ..., х_i.

Предполагается, что данная точка размещается на расстоянии радиуса влияния, тогда 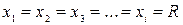и глубина воды в точке будет равна мощности водоносного пласта: .

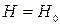Считается, что дебиты Q всех n колодцев одинаковы. Суммарный дебит n колодцев

. (11.64)

В результате всех предпосылок Форгеймером было получено уравнение для определения глубины в разных точках общей кривой депрессии при условии эксплуатации группы совершенных колодцев с одинаковым дебитом Q:

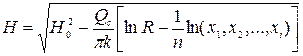. (11.65)

Выражение (11.65) позволяет определить глубину в разных точках общей кривой депрессии при условии эксплуатации группы совершенных колодцев с одинаковым дебитом Q.

Значение радиуса влияния R принимается, как для одиночного совершенного колодца при безнапорной фильтрации.

Полученная формула может быть использована для определения глубины воды в любом колодце, например для третьего колодца

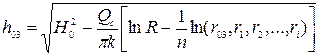, (11.66)

где 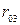- радиус третьего колодца; 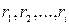- расстояние от третьего колодца до каждого из группы колодцев.

Уравнение (11.65) можно применить при условии, что группа колодцев приравнивается к большему (эквивалентному) колодцу. Приток воды к эквивалентному колодцу равен притоку группы n колодцев (см. рис. 11.14).

Радиус этого колодца

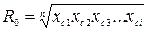; (11.67)

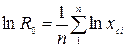, (11.68)

где 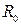- среднее геометрическое расстояние от каждого из n колодцев до центра их группы; 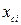- расстояние от центра до i-го колодца.

Глубина воды в большом колодце радиусом 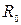равна 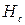. Приток воды к большому колодцу согласно формулам (11.65) и (11.68)

или . (11.69)

При расположении колодцев относительно равномерно по определенному контуру радиус «большого» колодца можно вычислить по формуле

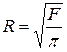, (11.70)

где F - площадь, находящаяся внутри контура размещенных в нем колодцев.

В случае когда колодцы размещаются в виде прямоугольника в плане с отношением сторон 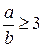, радиус «большого» колодца может быть определен по зависимости

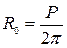, (11.71)

где Р - периметр прямоугольного контура группы колодцев.

Для ряда большого количества линейно расположенных несовершенных колодцев с расстояниями между ними 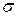(рис. 11.15) дебит отдельного колодца при напорной фильтрации в неограниченном пласте грунта и двустороннем притоке определяется по формуле

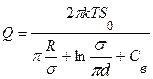. (11.72)

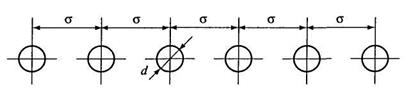
Рис. 11.15. Ряд трубчатых колодцев, расположенных линейно

Приток предлагается также находить по следующей формуле при условии :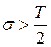

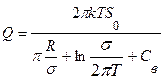. (11.73)

Дебит несовершенного колодца, находящегося в неограниченном безнапорном пласте грунта, может быть вычислен по формуле

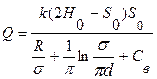, (11.74)

где 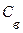- коэффициент дополнительного фильтрационного сопротивления несовершенного колодца (см. формулу (11.50)).

Для ряда колодцев, располагающихся по окружности радиусом 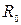, при расстоянии между ними 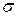и круговом питании приток к каждому трубчатому совершенному колодцу вычисляется по следующим формулам:

при напорной фильтрации

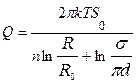; (11.75)

при безнапорной фильтрации

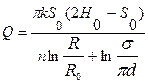, (11.76)

где R - радиус депрессии.

В случаях несовершенных колодцев в формулах (11.75) и (11.76) вводится дополнительное сопротивление 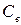(11.50):

например,

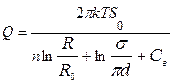. (11.77)

♦ Пример 11.4

Определить приток к водозаборной установке, состоящей из шести совершенных трубчатых колодцев, доведенных до напорного пласта из среднезернистого песка, мощностью Т = 30 м. Радиус влияния R = 350 м, понижение уровня воды в центре установки колодцев 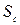= 40 м.

Схема расположения колодцев приведена на рис. 11.16.

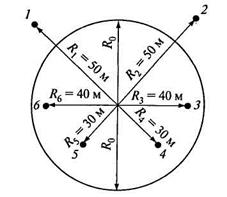
Рис. 11.16. Схема расположения группы колодцев

Радиус большого (эквивалентного) колодца согласно формуле (11.63)

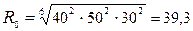м.

Коэффициент фильтрации k принимаем по табл. 11.1 для среднезернистых песков: м/с.

Суммарный приток к водозаборной установке согласно формуле (11.69)

м³/с

или

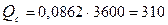м³/ч.

Приток к отдельному колодцу 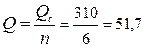м³/ч.

♦ Пример 11.5

Вычислить приток к установке для случая шести несовершенных колодцев (см. рис. 11.16) и определить их диаметр. Глубина погружения колодцев 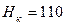м. Заглубление в напорный пласт t= 10 м. Понижение уровня воды в колодце принять 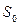= 50 м.

Диаметр колодцев определяется подачей вертикальных погружных насосов и притоком воды к колодцу.

По каталогу насосов при притоке к колодцу Q = 51,7 м³/ч первоначально выбирается насос ЭЦВ 10-63-100, а диаметр колодца принимаем d = 300 мм (подача Q = 63 м³/ч).

Приток воды к несовершенному колодцу, располагающемуся по окружности, вычисляется по формуле (11.77):

.

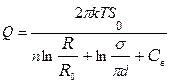Расстояние между колодцами 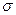для большого колодца радиусом 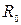= 39,3 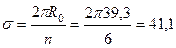м

м.

Дополнительное сопротивление на несовершенность колодцев 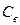согласно формуле (11.50)

.

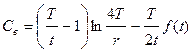Функциональная зависимость 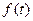находится по графику рис. 11.12 при ; .

.

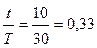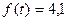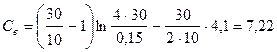Дебит колодца

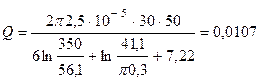м³/ч.

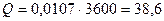м³/с.

Исходя из меньшего дебита колодца целесообразно подобрать насосы с подачей меньшей, принятой ранее.

♦ Пример 11.6

Шесть колодцев располагаются линейно. Расстояние между колодцами 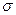= 20 м. Определить приток к водозаборной установке в случае совершенных и несовершенных колодцев. Параметры напорного пласта и колодцев принять в соответствии с предыдущим примером.

Дебит совершенного колодца при двустороннем притоке воды вычисляется по формуле (11.72) ( ):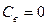

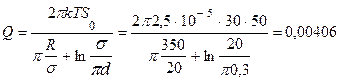м³/с;

м³/ч.

Дебит несовершенного колодца

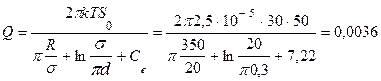м³/с;

м³/ч.

Дополнительное сопротивление на несовершенство 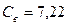(см. предыдущий пример).

Приток воды к установке 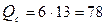м³/ч. Следует отметить, что при дебите 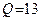м³/ч необходимо уточнить марку насоса для отбора (откачки) воды из колодца. Согласно каталогу насосов можно выбрать насос ЭЦВ 8-16-110 и диаметр колодца d = 200 мм. Кроме того, целесообразно знать необходимый расход водопотребления для определения, удовлетворяет ли он тому вычисленному притоку к водозаборной установке.