НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ГРУНТОВЫХ ВОД

Формула Дюпюи

Рассмотрим неравномерное безнапорное плавно изменяющееся движение грунтового потока воды в фильтрационном пласте грунта (рис. 11.3). Кривизна линий тока, изображенных на рисунке, весьма мала.

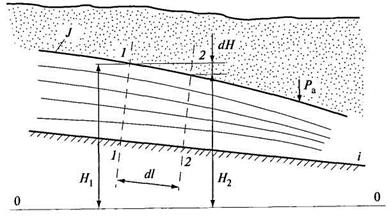
Рис. 11.3. Схема плавно изменяющегося движения фильтрационного потока

Так как кривизна линий тока невелика, то живые сечения можно считать плоскими. Расстояние между сечениями 1-1 и 2-2 для линий тока будет одинаковым и равным dl. Потери напора на участке dl относительно плоскости сравнения 0-0 равны dH. Для любой линии тока при переходе от сечения 1-1 к сечению 2-2 значение dH будет одинаково. Следовательно, при плавно изменяющемся неравномерном движении фильтрационного потока величина гидравлического (пьезометрического) уклона относительно всех точек рассматриваемых сечений, через которые проходят линии тока, является постоянной. Гидравлический уклон будет соответствовать уклону свободной поверхности воды в выбранной области фильтрации 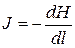. Если гидравлический (пьезометрический) уклон постоянен, то и скорости u в различных точках выбранного живого сечения фильтрационного потока будут одинаковы. Таким образом, средняя скорость в данном живом сечении фильтрационного потока будет равна скорости и в любой его точке:

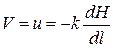(11.15)

Фильтрационный расход Q через живое сечение 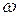, перпендикулярное линиям тока,

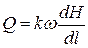(11.16)

Формула (11.16) для определения средней скорости в плоском вертикальном сечении при плавно изменяющемся движении фильтрационного потока в грунтах называется формулой Дюпюи.

Формула Дюпюи является частным случаем закона Дарси.

Из всего изложенного выше следует, что при неравномерном плавно изменяющемся движении фильтрационного потока гидравлический уклон и средняя скорость фильтрации в пределах выбранного поперечного сечения остаются постоянными по направлению фильтрационного движения в определенной области.

Формула Дюпюи позволяет определять среднюю скорость фильтрации и расход в плоском вертикальном сечении фильтрационного потока жидкости при его плавно изменяющемся ламинарном движении.