Операции булевой алгебры. Логические схемы.

1. Конъюнкция –логическое умножение, логическое И. Логическое умножение: операция, связывающая 2 и более высказывания с помощью союза «И»

ЗАКОН: Конъюнкция истинна тогда и только тогда, когда истинны ВСЕ входящие в нее высказывания.

Обозначается: И, Ù, ×

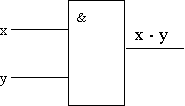Графически: Таблица истинности:

2. Дизъюнкция –логическое сложение, логическое ИЛИ. Логическое сложение: операция, связывающая два и более высказывания с помощью союза «ИЛИ»

ЗАКОН: Дизъюнкция истинна тогда и только тогда, когда истинно ХОТЯ БЫ ОДНО из входящих в нее высказываний.

Обозначается: ИЛИ, V, +

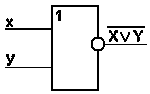
Графически: Таблица истинности:

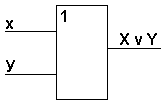
	Х	Y	X v Y

3. Инверсия. Логическое отрицание, логическое НЕ. Логическое отрицание – это присоединение частицы «НЕ» к сказуемому высказывания. (Петров- врач. Петров – не врач)

ЗАКОН: Если высказывание Х – истинно, то НЕ Х – ложно.

Обозначается: НЕ, 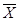, Х

Графически: Таблица истинности:

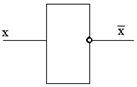
	Х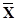

На основе использования основных логических схем строятся еще две логические схемы: Схема И-НЕ (элемент Шеффера) и схема ИЛИ-НЕ (элемент Пирса)

Схема И-НЕ состоит из элемента «И» и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом: 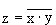, где 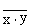читается как "инверсия x и y".

x	y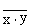

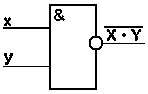
Схема ИЛИ-НЕсостоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.

x	y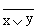

Связь между выходом z и входами x и y схемы записывают следующим образом: 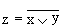, где 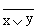, читается как "инверсия x или y".

(ПРИВЕСТИ ПРИМЕРЫ НА СОТАВЛЕНИЕ ТАБЛИЦ ИСТИННОСТИ, СХЕМ)