Математический маятник.
Механические колебания и волны
Колебаниями называются повторяющиеся движения или изменения состояния.
Всем колебаниям независимо от их природы присущи некоторые общие закономерности. В зависимости от характера взаимодействия колеблющийся системы с окружающими телами, различают колебания: свободные и вынужденные. Колебания распространяются в среде в виде волн
Свободные механические колебания
Свободными колебаниями называют такие колебания, которые совершаются без внешнего воздействия, за счёт первоначально полученной телом энергии. Характерными моделями таких колебаний является пружинный маятник (материальная точка на пружине)) и математический маятник (материальная точка на нерастянутой нити).
В этих примерах, колебания возникают за счёт первоначальной потенциальной энергии (отклонение материальной точки от положения равновесия и движения без начальной скорости), либо за счёт кинетической (телу сообщается скорость, в начальном положении равновесия), либо за счёт той и другой энергии.
Рассмотрим пружинный маятник

В положении равновесия, упругая система F1 уравновешивает силу тяжести mg.
Если растянуть пружину на расстояние х, то на материальную точку будет действовать большая сила упругости.
F=-kx (1), где k- коэффициент пропорциональности между силой и смещением, в данный момент – жестокость пружины показывает, что сила направлена в сторону положения равновесия
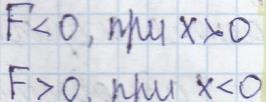
Математический маятник.
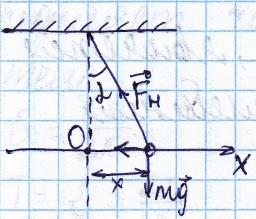
Он отклонён на небольшой угол α (Альфа), чтобы можно было считать траекторию движения точки прямой линии совпадении с траектории движения
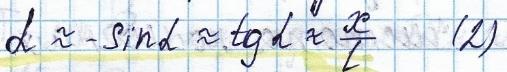
На точку действует сила натяжения нити FH .
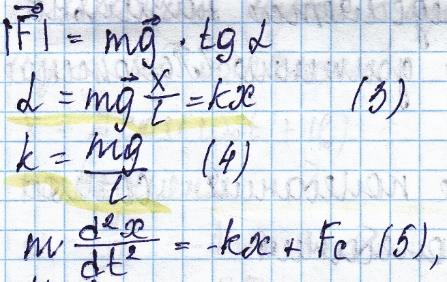
Fc – сила сопротивления точек
Дата добавления: 2015-12-29; просмотров: 983;
