Математический аппарат термодинамики
Основным математическим аппаратом термодинамики является теория дифференциальных пфаффовых форм от двух и более независимых переменных, а также методы преобразования частных производных от одной группы независимых переменных к другой. В общем случае дифференциальная форма записывается в виде
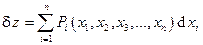
Здесь 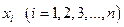 - набор независимых переменных (в термодинамике - набор независимых параметров состояния системы); dxi - дифференциалы независимых переменных, т.е. бесконечно малые изменения независимых параметров состояния;
- набор независимых переменных (в термодинамике - набор независимых параметров состояния системы); dxi - дифференциалы независимых переменных, т.е. бесконечно малые изменения независимых параметров состояния; 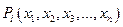 - заданные функции независимых переменных. Эти функции представляют собой либо свойства термодинамической системы, либо функции параметров. Выражение позволяет получить функцию
- заданные функции независимых переменных. Эти функции представляют собой либо свойства термодинамической системы, либо функции параметров. Выражение позволяет получить функцию 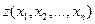 интегрированием этой дифференциальной формы вдоль некоторой гиперкривой в пространстве переменных
интегрированием этой дифференциальной формы вдоль некоторой гиперкривой в пространстве переменных 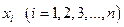 . Известно, однако, что в общем случае результат интегрирования , т.е. конкретный вид функции
. Известно, однако, что в общем случае результат интегрирования , т.е. конкретный вид функции 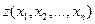 , будет зависеть как от выбранного начального состояния (0), так и от пути (γ) перехода системы из этого начального состояния до текущего, т.е. в общем случае решение следует писать в виде
, будет зависеть как от выбранного начального состояния (0), так и от пути (γ) перехода системы из этого начального состояния до текущего, т.е. в общем случае решение следует писать в виде 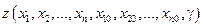 . Известно также, что существуют два типа дифференциальных форм, одна из которых, называемая неполным дифференциалом,характеризуется зависимостью решения
. Известно также, что существуют два типа дифференциальных форм, одна из которых, называемая неполным дифференциалом,характеризуется зависимостью решения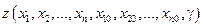 от пути интегрирования (γ) и другая, называемая полным дифференциалом, интеграл которого
от пути интегрирования (γ) и другая, называемая полным дифференциалом, интеграл которого 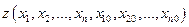 не зависит от выбора пути. Примеров, иллюстрирующих свойства полных и неполных дифференциалов, можно привести множество из различных областей физики, экономики и т.д. В частности, рассмотрим пример с автомобилем, перевозящим груз из какого-либо пункта А, находящегося на географической высоте hA, в пункт Б на высоте hБ. И пусть имеется множество маршрутов, соединяющих эти пункты. Тогда, как известно, работа по поднятию груза с высоты hA на высоту hБ в поле тяжести определится произведением веса груза на разность высот hБ– hA и не будет зависеть от маршрута, т.е. от пути. На каждом малом участке любого из маршрутов малые величины работы по поднятию груза определятся дифференциалом
не зависит от выбора пути. Примеров, иллюстрирующих свойства полных и неполных дифференциалов, можно привести множество из различных областей физики, экономики и т.д. В частности, рассмотрим пример с автомобилем, перевозящим груз из какого-либо пункта А, находящегося на географической высоте hA, в пункт Б на высоте hБ. И пусть имеется множество маршрутов, соединяющих эти пункты. Тогда, как известно, работа по поднятию груза с высоты hA на высоту hБ в поле тяжести определится произведением веса груза на разность высот hБ– hA и не будет зависеть от маршрута, т.е. от пути. На каждом малом участке любого из маршрутов малые величины работы по поднятию груза определятся дифференциалом 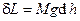 , который в данном случае будет полным. Что же касается таких величин, как затраты времени, топлива или стоимости перевозки, то они, очевидно, будут зависеть от выбранного маршрута, т.е. от его длины, состояния дорог, режима движения и даже от времени суток. Дифференциалы этих величин, т.е. их малые количества на малых участках разных маршрутов, будут неполными.
, который в данном случае будет полным. Что же касается таких величин, как затраты времени, топлива или стоимости перевозки, то они, очевидно, будут зависеть от выбранного маршрута, т.е. от его длины, состояния дорог, режима движения и даже от времени суток. Дифференциалы этих величин, т.е. их малые количества на малых участках разных маршрутов, будут неполными.
Условимся в дальнейшем для полных дифференциалов использовать традиционное обозначение 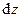 , а для неполных –
, а для неполных – 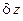 .
.
Мы будем в дальнейшем рассматривать так называемые простые термодинамические системы, состояние которых однозначно определяется заданием значений двух независимых переменных. В этом случае дифференциальная форма принимает более простой вид
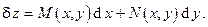
В математике существуют два признака полноты или неполноты дифференциальной формы:
· Интегральный – интеграл по любому замкнутому пути (контуру) от полного дифференциала равен нулю, т.е.
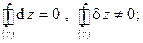
· Дифференциальный – равенство перекрёстных производных в случае полного дифференциала, т.е. если 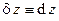 , то
, то
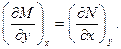
Интегральный признак позволяет утверждать, что результатом интегрирования неполного дифференциала от состояния (1) до состояния (2) будет некоторое число z12, величина которого зависит от выбора пути (γ), т.е.
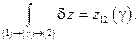
В случае же, если дифференциал является полным, то результат его интегрирования в тех же пределах не будет зависеть от пути (γ), а будет определяться только разностью значений функции z(x,y) в конечном (2) и начальном (1) состояниях:
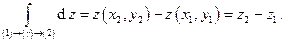
Большое прикладное значение в термодинамике имеет случай 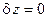 , т.е. когда
, т.е. когда
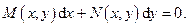
Это выражение есть не что иное, как обыкновенное дифференциальное уравнение первого порядка
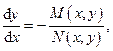
решение которого y=y(x,C) геометрически представляет собой семейство кривых на плоскости переменных (x,y), каждая из которых характеризуется своим значением параметра C. Оказывается, что интегральные кривые в случае двух независимых переменных никогда не пересекаются, кроме, возможно, дискретного набора точек или конечного набора линий. А это говорит о том, что дифференциальная форма 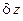 , не будучи полным дифференциалом, всегда может быть преобразована в полный умножением на подходящим образом подобранную или вычисленную функцию
, не будучи полным дифференциалом, всегда может быть преобразована в полный умножением на подходящим образом подобранную или вычисленную функцию 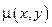 , называемую интегрирующим множителем, таким образом, что
, называемую интегрирующим множителем, таким образом, что
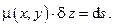
В случае трёх и более независимых переменных существование интегрирующего множителя уже не является обязательным, а возможность обращения дифференциальной формы в полный дифференциал будет диктоваться только физическими соображениями.
Для непрерывной однозначной функции z(x,y) всегда можно записать полный дифференциал в виде суммы частных дифференциалов
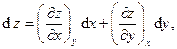
где частные производные 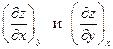 обычно связаны с физическими свойствами вещества и имеют смысл изменения какого-либо из параметров, например z, при изменении другого параметра, например x, на единицу при условии, что третий параметр, например y, поддерживается постоянным. Во многих случаях экспериментальное нахождение физических свойств веществ, т.е. соответствующих частных производных, либо является весьма трудоёмким, либо вообще невозможно. Мощь термодинамического метода состоит в том, что, опираясь на самые общие принципы, начала, законы природы и используя формализм простейших операций с дифференциальными формами, термодинамика позволяет описывать и предсказывать поведение самых различных термодинамических систем при тех или иных воздействиях и при соблюдении тех или иных условий. В частности, пусть производные
обычно связаны с физическими свойствами вещества и имеют смысл изменения какого-либо из параметров, например z, при изменении другого параметра, например x, на единицу при условии, что третий параметр, например y, поддерживается постоянным. Во многих случаях экспериментальное нахождение физических свойств веществ, т.е. соответствующих частных производных, либо является весьма трудоёмким, либо вообще невозможно. Мощь термодинамического метода состоит в том, что, опираясь на самые общие принципы, начала, законы природы и используя формализм простейших операций с дифференциальными формами, термодинамика позволяет описывать и предсказывать поведение самых различных термодинамических систем при тех или иных воздействиях и при соблюдении тех или иных условий. В частности, пусть производные 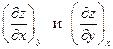 сравнительно легко измеряются на опыте, а свойство
сравнительно легко измеряются на опыте, а свойство 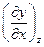 для своего измерения требует существенных затрат времени или средств или просто невозможно. Но из , полагая z=const, dz=0, имеем
для своего измерения требует существенных затрат времени или средств или просто невозможно. Но из , полагая z=const, dz=0, имеем
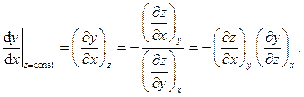
В термодинамике часто оказывается полезным так называемое преобразование Лежандра, основанное на известной формуле дифференциального исчисления
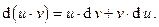
Это преобразование позволяет вводить в рассмотрение новые функции состояния, которые могут оказаться более удобными в практических расчетах и/или иметь более ясный и содержательный физический смысл. Непосредственное использование преобразования Лежандра будет показано на конкретных задачах термодинамики в ходе дальнейшего изложения.
| Р1.Т2 | Параметры состояния.0.3 часа |
Для количественного описания поведения термодинамической системы вводят так называемые параметры состояния, под которыми понимаются величины, численные значения которых однозначно определяют состояние системы в заданный момент времени. Параметры состояния, их смысл и число могут быть найдены только на основании опыта. Термодинамический, т.е. феноменологический, подход требует только, чтобы параметры состояния могли быть измеримы опытным путём с помощью макроскопических приборов. Перечислим некоторые из возможных параметров состояния термодинамической системы, измерение которых доступно современными приборами: 1) координаты центра инерции системы; 2) скорость центра инерции; 3) угловая скорость вращения системы; 4) масса системы; 5) объём; 6) температура; 7) давление; 8) диэлектрическая проницаемость; 9) магнитная проницаемость; 10) вектор электрической поляризации; 11) магнитный момент; 12) концентрации химических элементов в смеси и т.д.
Как видим, число макроскопических параметров достаточно велико и, строго говоря, не определено, однако далеко не все из них имеют существенное значение для термодинамики. Некоторые из них, такие как положение центра инерции, его скорость и угловая скорость вращения, могут быть вообще исключены из рассмотрения, так как согласно известным положениям классической механики всегда имеется возможность перейти в систему отсчёта с началом в центре инерции системы и жёстко связанную с ней. Численные значения некоторых параметров во множестве прикладных задач термодинамики либо могут считаться равными нулю, либо постоянными с достаточной степенью точности, либо вообще выпадают из рассмотрения. Таковы, например, электрические и магнитные свойства большинства веществ в отсутствие или при наличии слабых электрического и магнитного полей, а также концентрации компонентов в нереагирующей смеси.
Оказалось, что в простейшем случае любая термодинамическая система должна обладать четырьмя макроскопическими параметрами, а именно: массой M, объёмом V, давлением p и температурой T. Рассмотрим каждый из них более подробно.
Масса. В современной физике масса имеет два определения. С одной стороны, под массой понимается мера инертности тела, т.е. способность тела приобретать то или иное ускорение под действием силы, которая появляется в уравнении второго закона Ньютона как коэффициент пропорциональности между силой и ускорением. Такая масса носит название инерционной. С другой стороны, масса выступает в роли источника гравитационного притяжения в законе всемирного тяготения Ньютона и называется в данном случае гравитационной. Решая задачи небесной механики, Ньютон идентифицировал эти два понятия, опираясь на опыты Г.Галилея по изучению законов падения тел в поле тяжести Земли. Проведенные в настоящее время весьма точные измерения показали, что инерционная и гравитационная массы отличаются не более чем на 10-12%. Постулат о точном равенстве инерционной и гравитационной масс лежит в основе общей теории относительности А.Эйнштейна - теории гравитации.
В системе единиц СИ масса M измеряется в килограммах (кг), эталон которого в форме цилиндра из платиноиридиевого сплава хранится в Международном бюро мер и весов в Севре под Парижем. Примерно один килограмм составляет массу 1 литра (1 дм3) дистиллированной воды при температуре 15оС.
Объём. Измерение объёма представляется наиболее простой операцией, даже если форма оболочки термодинамической системы весьма сложна. В этом случае объём системы можно измерить по объёму вытесненной жидкости, однако в любом случае измерение объёма связано с необходимостью измерения длин. В современной физике за единицу длины принимается расстояние, пройденное светом в вакууме за 1/299792458 секунды, при этом за 1 секунду принимается время, в течение которого электромагнитные волны, излучаемые атомом цезия Сs133 при квантовом переходе между линиями сверхтонкой структуры основного состояния, совершают 9192631770 колебаний. В системе единиц SI это расстояние принимается за 1 метр. Эталон метра из платиноиридиевого сплава также хранится в Международном бюро мер и весов в Севре под Парижем.
Давление. Давление в термодинамике определяется так же, как и в механике, т.е. как отношение силы, действующей нормально на единицу площади выбранной поверхности со стороны термодинамической системы. В термодинамике под поверхностью понимается поверхность оболочки, ограничивающей термодинамическую систему. За единицу давления в системе единиц СИ принимается паскаль (Па), определяемый как сила в 1 ньютон (1 Н), действующая нормально на поверхность площадью 1 м2. Таким образом, по определению
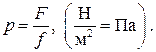
Паскаль (Па) как единица давления является не очень удобной величиной в повседневной человеческой деятельности ввиду своей малости, поэтому на практике обычно используют более крупную единицу давления – бар, определяемую соотношением
1 бар = 100000 Па = 105 Па.
В силу исторических традиций единицы давления различны в разных областях человеческой деятельности. Перечислим их, не останавливаясь на происхождении каждой из них. В метеорологии, медицине и других в качестве единицы давления используется 1 миллиметр ртутного столба (мм рт.ст.), т.е. вес ртути высотой 1 мм, налитой в цилиндр площадью поперечного сечения f , приходящийся на единицу площади этого сечения, т.е.
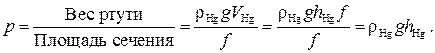
Очевидно, что эта формула справедлива и для любой другой жидкости, лишь бы её можно было считать несжимаемой.
Определение позволяет найти связь между единицами давления мм рт.ст. и Па:
1 мм рт.ст = 133.3 Па .
Для измерения малых перепадов давления используется более мелкая единица – миллиметр водяного столба (мм вод.ст.), величина которого легко находится из :
1 мм вод.ст. = 9.81 Па .
В физических исследованиях, в технике, аэродинамике, гидрометеорологии весьма часто в качестве единицы давления используется так называемая физическая атмосфера, определяемая равенствами
1 физ.атм. = 760 мм рт.ст. = 10329 мм вод.ст. = 101325 Па = 1.013 бар.
В технике также широко используется единица давления, называемая технической атмосферой и определяемая как сила в один килограмм, приходящаяся на 1 см2 поверхности. В частности, большинство технических манометров градуированы в технических атмосферах. Из определения технической атмосферы легко находим
1 тех.атм. = 98100 Па = 0.98 бар = 736 мм рт.ст.
Отметим также
1 бар = 750 мм рт.ст.
С точки зрения молекулярно-кинетической теории, давление, оказываемое газом на оболочку, представляет собой усредненный импульс, передаваемый стенке сталкивающимися с ней молекулами, в единицу времени. Так определённое давление называется абсолютнымpабс или pа .
Приборы, предназначенные для измерения давления, называются манометрами. При этом прибор, предназначенный для измерения атмосферного давления, носит название барометра.Первый известный в истории барометр был сконструирован итальянским учёным Э.Торричелли в 1644 году и с тех пор не претерпел никаких принципиальных изменений. Этот барометр представлял собой запаянную с одного конца стеклянную трубку длиной около одного метра, заполненную ртутью и опущенную открытым концом вертикально в сосуд с ртутью. Оставшийся в трубке столб ртути высотой около 750 мм уравновешивается атмосферным давлением, величину которого после опытов Торричелли стали измерять непосредственно в миллиметрах этого ртутного столба. Позднее был изобретён барометр, называемый анероидом, конструкция которого оказалась менее опасной и более удобной в мореплавании. Барометр-анероид представляет собой вакуумированный герметически запаянный диск из сравнительно тонкой латуни или бронзы. Изменение атмосферного давления приводит к деформации оснований диска, а величина этой деформации, пропорциональная атмосферному давлению, передаётся на указательную стрелку. Очевидно, что ртутный барометр Торричелли и барометр-анероид ввиду наличия вакуума показывают абсолютное давление атмосферного воздуха, называемое обычно барометрическимpбар, или pб, или B.
В технике большое распространение получили манометры, главной особенностью которых является то, что независимо от конкретной конструкции все они измеряют не абсолютное давление в сосуде с газом, а так называемое избыточное давление pизб или pи , т.е. разность между абсолютным давлением в сосуде и давлением атмосферы:
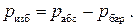
Температура
История становления понятия температуры в физике, технике и в повседневной жизни связана со многими событиями, на описании которых мы не имеем здесь возможности останавливаться. Интересующихся можно отослать к популярной литературе. Мы здесь остановимся лишь на вопросах, имеющих существенное значение для понимания категории температуры и на методах и способах её измерения.
Можно дать по меньшей мере четыре определения температуры:
· температура есть мера нагретости тела; при этом под нагретостью понимают субъективное ощущение теплоты или холода;
· температура есть показания специального прибора, именуемого термометром;
· температура есть величина, пропорциональная средней кинетической энергии молекул;
· различные комбинации трёх первых определений.
Все эти определения, тем не менее, не обладают необходимой в любой науке, тем более "строгой", точностью, однозначностью в отличие, например, от определений массы или объёма.
Несмотря на это, введение понятия, аналогичного температуре, было продиктовано всей практикой человеческой и, в частности, научной деятельности. Отвлекаясь от чисто субъективных ощущений тепла и холода, было замечено, что состояния двух тел, приведенных в контакт друг с другом без видимого силового взаимодействия, изменяются и далее с течением времени остаются неизменными. Такой контакт был назван тепловым, а тепловое взаимодействие понималось как "перетекание" от одного тела к другому некоторой невесомой жидкости без цвета и запаха, названной теплородом. Гипотеза теплорода просуществовала вплоть до второй половины XIX века и была отвергнута только под давлением экспериментальных фактов, которые никак не могли быть ею объяснены. При этом под температурой понимался некий "потенциал", т.е. некоторая "высота", с которой, по аналогии с потоком воды в поле тяжести Земли, теплород "стекает" в области с меньшим потенциалом, с меньшей температурой. Несмотря на кажущуюся наивность этих представлений с современной точки зрения, гипотеза теплорода на первых порах оказалась довольно плодотворной и позволила, например, Сади Карно в 1824 году прийти к выводам, лежащим в основе так называемого второго начала термодинамики и понятия энтропии. Случай с температурой является уникальным в научной практике, так как это была первая из физических величин, которую научились измерять, не зная, что это такое. Тем не менее следует заранее сказать, что ни один из термометров, т.е. ни один из приборов, предназначенных для измерения температуры, не измеряет непосредственно температуру. Любой термометр измеряет только тот или иной эффект, связанный с изменением температуры. Например, ртутный, спиртовый или газовый термометры позволяют измерять изменение объёма с изменением температуры при постоянном давлении, термометр сопротивления фиксирует изменение электрического сопротивления с изменением температуры, пирометр связывает с температурой яркость тел, нагретых до больших температур и т.д. Строгое определение температуры и температурной шкалы в рамках термодинамики даёт только второе начало термодинамики в связи с рассмотрением цикла Карно. Такое же строгое обоснование имеет понятие температуры в статистической физике, где температура (называемая абсолютной) оказывается величиной, пропорциональной параметру, характеризующему распределение вероятности кинетической энергии огромного числа хаотически движущихся молекул, составляющих газ.
Происхождение понятий "градус" и "температура" восходит к древнегреческой медицине. Живший во II веке н.э. древнегреческий врач Гален учил, что лекарства следует классифицировать по градусам (ступеням): градус тепла, градус холода, градус влажности, градус сухости. Смеси лекарств (по латыни temperatura) давали различные "градусы". Первые приборы, предназначенные для измерения температуры (термометры), были сконструированы Галилеем (около 1597 г.) и основывались на изменении объёма газов при нагревании. Основная трудность при конструировании термометров состояла в выборе шкалы, т.е. в возможности сравнения показаний термометров различных конструкций и различных принципов действия. Первая температурная шкала была предложена в 1724 году голландским стеклодувом Д.Фаренгейтом, который приписал значение 0оF температуре самой суровой зимы в Голландии в 1709 году, 32oF - температуре смеси льда с водой, 98oF - нормальной температуре человеческого тела и 212oF - температуре кипения воды. Температурная шкала Фаренгейта до сих пор ещё в ходу в Англии, США и некоторых других странах. Во Франции (около 1740 г.) вошла в употребление шкала Реомюра, в которой в качестве опорных (реперных) точек выбирались точки замерзания воды (0оR) и кипения воды (80оR). Шведский физик Андерс Цельсий предложил свою шкалу в 1742 году. В ней также в качестве реперных выбирались точки замерзания и кипения воды, однако Цельсий предложил считать температуру кипения воды равной 0, а температуру замерзания воды равной 100 градусам. Шкала Цельсия разбивалась на 100 равных частей между этими двумя реперными точками. Позднее его современник Карл Линней «перевернул» эту шкалу. Оказалось, однако, что такая шкала также обладает недостатками, связанными с зависимостью коэффициента расширения воды (и других термометрических жидкостей) от температуры. В 1968 году была принята международная практическая температурная шкала (МПТШ-68), основанная на шкале Цельсия, разбиение на градусы в которой произведено не равномерно, а в зависимости от коэффициента расширения воды. Такая температурная шкала носит название стоградусной и имеет обозначение tоС.
И, наконец, в 1848 году английский физик Вильям Томсон (лорд Кельвин) ввёл так называемую абсолютную температурную шкалу, называемую также шкалой Кельвина, в которой за начало отсчёта температуры принимается абсолютный нуль, т.е. температура, при которой теоретически прекращаются все возможные виды движения частиц в теле. В остальном введённая В.Кельвином абсолютная температурная шкала совпадала со шкалой Цельсия. В современной физике в качестве реперной точки выбирается тройная точка воды, т.е. состояние воды, в котором лёд, жидкость и пар сосуществуют в равновесии одновременно. В шкале Кельвина тройной точке воды приписывается температура 273.16 К. Тогда точка замерзания воды (таяния льда) имеет температуру 273.15 К.
Приведём для справок связь между различными температурными шкалами, употребляемыми в настоящее время в разных странах или в различных областях человеческой деятельности:
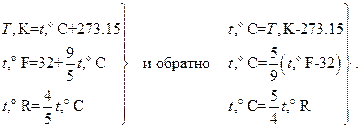
| Р1.Т3 | Экстенсивные и интенсивные величины. Удельные параметры | 0.2 часа |
Величины, характеризующие любую систему, могут быть разделены на две категории. Первая из них объединяет характеристики, численные значения которых пропорциональны массе системы. Такие величины называют экстенсивными. Вторая объединяет так называемые интенсивныевеличины, численные значения которых не пропорциональны массе системы, а имеют отношение ко всей системе в целом.
Экстенсивные величины обладают свойством аддитивности, т.е. значение экстенсивной величиныдля всей системы в целом равно арифметической сумме этих величин для отдельных частей системы. Интенсивные величины свойством аддитивности не обладают.
Примерами экстенсивных величин в термодинамике являются: 1) масса 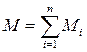 ; 2) объём
; 2) объём 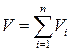 ; 3) внутренняя энергия (о ней речь пойдёт ниже)
; 3) внутренняя энергия (о ней речь пойдёт ниже) 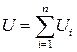 и другие.
и другие.
Аддитивными, т.е. экстенсивными, величинами являются также работа и количество теплоты.
Замечание. Перечисленные выше величины, строго говоря, являются аддитивными только в случае систем, отдельные части которых не взаимодействуют друг с другом ни в каком отношении. Такими системами являются, например, идеальные газы, о которых мы будем говорить позднее. Если же речь идёт, в частности, о жидкостях, то во внутреннюю энергию должна быть включена энергия поверхностного натяжения, величина которой пропорциональна не массе жидкости, а площади её внешней поверхности, а поверхность, как известно, не прямо пропорциональна объёму (массе) тела. В этом случае внутренняя энергия уже не будет аддитивной величиной. То же относится к работе, теплоте и др.
И ещё одно замечание. Строго говоря, и сама масса системы не является аддитивной величиной, если учитывать эффекты специальной и общей теории относительности. Как известно, при больших скоростях, сравнимых со скоростью света, масса зависит от скорости. Масса заметно меняется также в ядерных реакциях, где энергия взаимодействия чрезвычайно велика.
Часто вводят в рассмотрение удельные величины, т.е. экстенсивные параметры, отнесённые к единице массы системы. Таковы, например, удельный объём 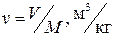 , удельная внутренняя энергия
, удельная внутренняя энергия 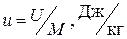 и т.д. Следует отметить, что удельные величины уже являются интенсивными и свойством аддитивности не обладают.
и т.д. Следует отметить, что удельные величины уже являются интенсивными и свойством аддитивности не обладают.
| Р2 | Термическое уравнение состояния. Идеальный газ. Смеси идеальных газов. 2 часа | |
| Р2.Т1 | Термическое уравнение состояния. | 0.5 часа |
В дальнейшем, если не будет оговорено особо, мы будем рассматривать термодинамические системы с постоянной массой, так называемые закрытые системы. В этом случае система будет характеризоваться только тремя термодинамическими параметрами: давлением p, температурой T и объёмом V. Такие системы называются простыми. Опыт показывает, что эти три параметра не являются независимыми, они связаны некоторой функциональной зависимостью
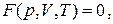
называемой термическим уравнением состояния. Явный вид термического уравнения состояния в рамках термодинамики получен быть не может. Эта зависимость различна для разных веществ и может быть найдена либо опытным путём, либо с помощью модельных теорий, например, с помощью методов статистической физики, в основе которой лежит представление о молекулярном строении вещества.
С геометрической точки зрения выражение для термического уравнения состояния представляет собой некоторую поверхность в системе прямоугольных координат (p,V,T), которая называется термодинамической поверхностью. Вид термодинамической поверхности зависит от вещества и его агрегатного состояния, однако любая из этих поверхностей не может иметь самопересечений, что следует из однозначности зависимости состояния системы от значений двух её независимых параметров. Для удобства графического изображения вместо трёхмерной системы координат (p,V,T) используют так называемые термодинамические диаграммы, т.е. плоские системы прямоугольных координат (p,V), (p,T) или (V,T), на которых недостающие параметры представляются в виде семейств непересекающихся линий T=const, V=constили p=constсоответственно.
В случае, если один из параметров в термическом уравнении состояния может быть выделен явно, его можно записать в одном из трёх видов:
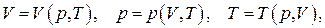
что во многих случаях является значительно более удобным.
| Р2.Т2 | Идеальный газ. Реальные газы | 0.8 часа |
Наиболее распространёнными веществами, используемыми в современных тепловых двигателях в качестве рабочих тел, являются атмосферный воздух и вода. Это связано, во-первых, с их большой распространённостью в природе и, во-вторых, с их относительно малой агрессивностью по отношению к конструкционным материалам. Этим объясняется большое количество экспериментальных данных по теплофизическим свойствам воздуха и воды.
Результаты опытных данных по свойствам воздуха и других газов при условиях, близких к атмосферным, были обобщены в виде так называемых газовых законов, носящих имена учёных, внесших наибольший вклад в эти исследования.
1. Закон Бойля - Мариотта
В 1661 году английский физик Р. Бойль и в 1676 году французский физик Э.Мариотт экспериментально установили обратно пропорциональную зависимость давления воздуха и других газов от объёма при постоянной температуре, что математически записывается в виде
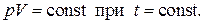
2. Закон Гей-Люссака.
Французский физик и химик Ж.Л. Гей-Люссак в 1802 году на основании опытных данных установил линейную зависимость объёма газов от температуры при постоянном давлении, т.е.
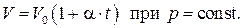
Постоянная 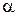 оказалась одинаковой для всех исследованных газов и по современным данным составляет
оказалась одинаковой для всех исследованных газов и по современным данным составляет
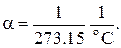
Закон Шарля
В 1787 году французский физик Ж.А.Ц. Шарль установил закон изменения давления газов с изменением температуры при постоянном объёме. Этот закон, так же, как и закон Гей-Люссака, описывается линейной зависимостью давления от температуры
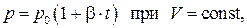
причём постоянная 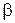 практически совпадала с постоянной
практически совпадала с постоянной 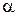 в законе Гей-Люссака. Позднее более точные измерения показали, что эти постоянные одинаковы.
в законе Гей-Люссака. Позднее более точные измерения показали, что эти постоянные одинаковы.
Закон Авогадро
Этот закон, сформулированный итальянским физиком и химиком А.Авогадро в 1811 году, гласит: при одинаковых температурах и давлениях одинаковые объёмы любых газов содержат одно и то же число молекул. Исходя из сформулированного им же закона о пропорциональности объёмов и масс вступающих в химическую реакцию газов, Авогадро удалось также вычислить число молекул, содержащихся в одном киломоле любого газа, так называемую постоянную(или число) Авогадро:
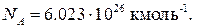
В терминах макроскопических параметров закон Авогадро формулируется следующим образом: один киломоль любого газа при нормальных физических условиях занимает один и тот же объём, равный 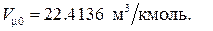
За нормальные физические условия (НФУ) принимаются стандартные значения давления и температуры, близкие к обычным атмосферным условиям в средних широтах северного полушария:
НФУ: 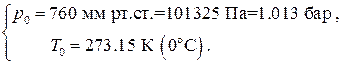
Перечисленные выше газовые законы позволяют записать термическое уравнение состояниядля газов. Для этого запишем полный дифференциал объёма V системы как функции двух независимых переменных – давления p и температуры t:
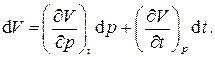
Частные производные, входящие в это выражение, легко находятся из математических записей законов Бойля - Мариотта и Гей-Люссака :
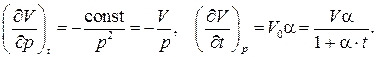
Подставляя эти частные производные в дифференциал объёма 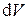 и разделив его на V, получим дифференциальное уравнение для V с разделёнными переменными
и разделив его на V, получим дифференциальное уравнение для V с разделёнными переменными
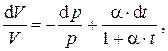
решение которого есть
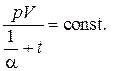
Величина 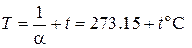 представляет собой температуру, нулевое значение которой по шкале Цельсия соответствует –273.15оС. Такая температурная шкала была предложена В.Кельвином и носит название абсолютной. Таким образом, решение может быть написано в виде объединённого закона газового состояния
представляет собой температуру, нулевое значение которой по шкале Цельсия соответствует –273.15оС. Такая температурная шкала была предложена В.Кельвином и носит название абсолютной. Таким образом, решение может быть написано в виде объединённого закона газового состояния
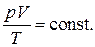
Это равенство неточное, так как оно получено на основании экспериментов и применимо в условиях, сравнительно близких к атмосферным.
Гипотетический газ, в точности подчиняющийся термическому уравнению состояния, называется идеальным. Это есть термодинамическое определение идеального газа. С молекулярно-кинетической точки зрения идеальным газом называется совокупность большого числа (порядка числа Авогадро) хаотически движущихся не взаимодействующих между собой материальных точек. Методами статистической физики, т.е. совместного использования уравнений движения и теории вероятностей, показывается, что эти два определения идеального газа, термодинамическое и молекулярно-кинетическое, эквивалентны, если под давлением p понимать средний импульс, переносимый хаотически движущимися молекулами на стенку в единицу времени, а под абсолютной температурой T – величину, пропорциональную средней кинетической энергии молекул.
Произвольная постоянная в уравнении состояния идеального газа может быть найдена с использованием закона Авогадро. В самом деле, если уравнение справедливо для любого состояния идеального газа, значит, оно справедливо и для состояния при нормальных физических условиях (НФУ). Таким образом, можно написать
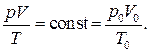
Объём данной массы газа M может быть выражен через его мольный объём
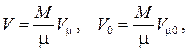
где 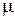 есть молекулярная (молярная) масса газа, а
есть молекулярная (молярная) масса газа, а 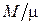 – число киломолей газа. Подставляя объём V0 в , получаем
– число киломолей газа. Подставляя объём V0 в , получаем
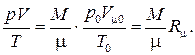
Комплекс
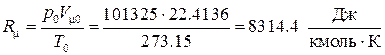
называется универсальной газовой постоянной. Таким образом, термическое уравнение состояния для идеального газа принимает вид
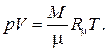
Это уравнение носит название уравнения Менделеева - Клапейронаи весьма широко используется во многих разделах физики, в технике, аэродинамике, метеорологии и т.д.
Отношение
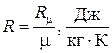
называется газовой постоянной для данного газа. С использованием этой величины термическое уравнение состояния записывается в виде
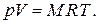
Уравнение состояния удобно записывать для одного килограмма газа, используя понятие удельного объёма
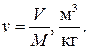
В этом случае уравнение состояния имеет вид
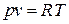
или
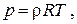
где 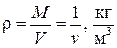 – плотность газа.
– плотность газа.
Термическое уравнение состояния позволяет найти связь между различными термическими коэффициентами, характеризующими упругие и термические свойства газов. Для идеального газа эти коэффициенты легко выражаются через параметры:
· температурный коэффициент расширения
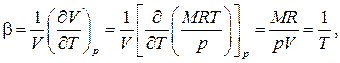
· изотермический коэффициент упругости
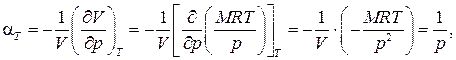
· коэффициент давления
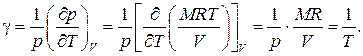
Для нахождения связи между этими тремя коэффициентами воспользуемся общей формулой , положив в ней 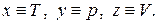 Тогда получаем
Тогда получаем
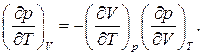
Используя определения термических коэффициентов –, находим искомую связь:
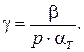
Реальные газы
Приведём справочные данные по уравнениям состояния газов и жидкостей по степени их усложнения (взято из Thermodynamique & energetique par Lucien Borel, Presses Polytechniques ROMANDES, LOSANNE, Ecoles polytechnique fédérale, 1984).
1. Совершенный газ(Gaz parfait)
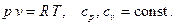
2. Идеальный газ (Gaz semi-parfait, gaz idéal)
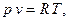
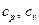 – возрастающие функции температуры.
– возрастающие функции температуры.
3. Газ Ван-дер-Ваальса (Fluide de Van der Waals)
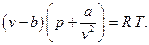
4. Газ Клаузиуса (Fluide de Clausius, 1880)
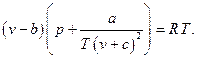
Здесь 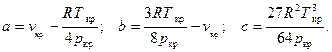
Это приближение справедливо с достаточной степенью точности при
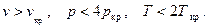
И напротив приближение становится грубым для парообразного состояния в области высоких температур и давлений и в области жидкости.
5. Газ Редлиха – Квонга (Fluide de Redlich – Kwong, 1949)
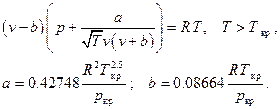
6. Газ Битти – Бриджмена (Fluide de Beattie – Bridgeman, 1928)
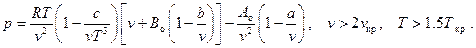
Это уравнение совершенно неприменимо вблизи критической точки.
7. Газ Бенедикта – Вебба – Рубина (Fluide de Benedict – Webbe – Rubin, 1951)
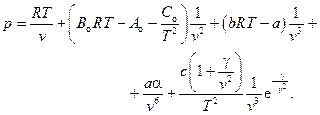
Справедливо для углеводородов при 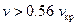 . Константы определяются экспериментально.
. Константы определяются экспериментально.
8. Газ Лан-Бореля (Fluide de Lan-Borel, 1979)
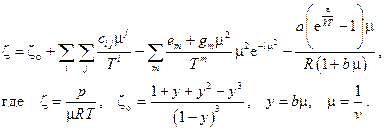
Показатели степени 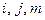 зависят от вида газа и определяются экспериментально. В частных случаях водяного пара и метана уравнение состояния записывается в виде
зависят от вида газа и определяются экспериментально. В частных случаях водяного пара и метана уравнение состояния записывается в виде
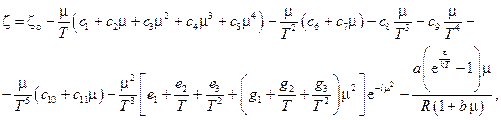
где 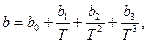 k – постоянная Больцмана.
k – постоянная Больцмана.
Это есть полуэмпирическое уравнение с 24-мя эмпирическими константами, базирующееся, с одной стороны, на молекулярной теории твёрдых сфер и, с другой стороны, на экспериментальных измерениях термодинамических свойств, таких как удельная теплоёмкость, коэффициент Джоуля–Томсона и скорость звука. Это уравнение даёт прекрасную точность в жидкой и газообразной областях для температур 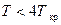 и даёт удовлетворительные результаты в интервале температур
и даёт удовлетворительные результаты в интервале температур 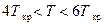 при любых давлениях. Оно описывает фазовые переходы и достаточно удобно для численных расчётов.
при любых давлениях. Оно описывает фазовые переходы и достаточно удобно для численных расчётов.
| <== предыдущая лекция | | | следующая лекция ==> |
| Подключение проводов к разъемам | | | Сетчатая, диффузная, или асинаптическая нервная система. |
Дата добавления: 2015-12-22; просмотров: 2348;
