Електричні властивості ПК.

В основу класифікації електричних властивостей ПК покладені морфологічні особливості пористого матеріалу, відмінності у величині пористості та утворенні збіднених областей в кремнієвій монокристалічній матриці. Класифікація електричних властивостей ПК передбачає поділ пористого матеріалу на чотири групи (рис.6.8), кожна з яких має індивідуальний набір властивостей.

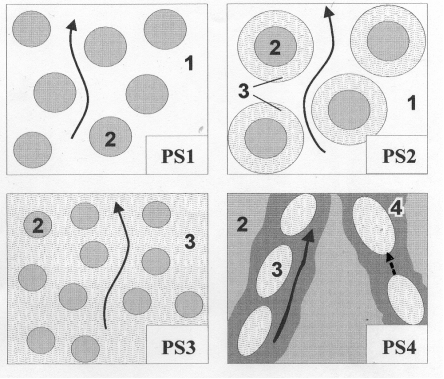
Рис.6.8.. Схематичне зображення процесів переносу носіїв у ПК різних груп. 1 - вихідна монокристалічна матриця, 2 - пори, 3 - збіднені області, 4 - фаза продуктів електрохімічних реакцій.

До першої групи (PS1) відноситься пористий матеріал, у якого збіднені області або відсутні або слабо виражені. Такий приклад описаний при формуванні ПК на сильно легованих сурмою кремнієвих пластинах при пористості 8-27 %. Перенесення носіїв заряду в такому ПК відбувається відповідно до теорії ефективного середовища в моделі «кремній + пори».

Другу групу (PS2) утворюють пористі структури, у яких великі пори далеко відстоять одна від одної і тому збіднені області навколо пор не перекриваються. Прикладом є макропористий кремній з пористістю 5-10 %, отриманий на слабо легованих фосфором пластинах. Холівські вимірювання свідчили, що концентрація електронів в області навколо пір зменшується, а збільшення питомої опору ПК в цьому випадку не відповідає теорії ефективного середовища для вагової пористості, але перебуває в узгодженості з цією теорією при обліку додаткового обєму, що є зайнятий збідненими областями. Перенос електронів в PS2 пов'язаний з рухом носіїв по низькоомним незбідненим ділянкам кремнієвої матриці у відповідності з теорією ефективного середовища в моделі « кремній + пори + збіднені області».

У третю групу (PS3) входять пористі структури з сильно розвиненою мережею дрібних пор, що мають відносно невисокий показник пористості (менше 40 %). Збіднені області сусідніх пор (за рахунок малої відстані між стінками пор) перекриваються і весь монокристалічний остов представляє собою коралоподібну структуру, що складається в загальному випадку з областей з різним ступенем збіднення, а в граничному випадку - з кремнію з власною провідністю. Прикладом PS3 є мезопористий кремній з малою пористістю, сформований на p+-Si. Дрейф носіїв заряду здійснюється по високоомній кремнієвій матриці в рамках моделі флуктуюючого потенційного рельєфу.

Четверта група (PS4) включає в себе структури з високою пористістю (більше 45-50%), для яких структура матеріалу, а, отже, і механізм провідності, зазнають значних змін. У такому ПК нанокристаліти кремнію розмірами від одиниць до десятків нанометрів є областями кремнію, що не розчинилися, і є оточеними продуктами електрохімічних реакцій. При розмірах кристалітів менше 4 нм в них починають виникати квантово-розмірні ефекти, що призводять до квантування енергетичного спектру носіїв, до збільшення ширини забороненої зони до 1,8-2,9 еВ і до зменшення діелектричної проникності. Для нанокристалітів кремнію характерні процеси збіднення, концентрація носіїв у них 10¹⁰ - 10¹³ cм ^-3, однак величина провідності вже визначається не стільки концентрацією носіїв, скільки характером переносу. Провідність в такій структурі сильно залежить від питомого опору середовища продуктів електрохімічних реакцій і може здійснюватися по матриці, що оточує кристаліти (близької за властивостями до α - Si: H ) або за допомогою міжкристалічних перескоків, коли питомий опір середовища, що оточує нанокристаліти досить великий. Останній випадок може мати місце при формуванні продуктів електрохімічних реакцій у вигляді високоомних оксидів SiO_x.

Запропонована класифікація електричних властивостей ПК дозволила пояснити експериментально спостережуване різноманіття властивостей переходів ПК / метал і ПК / Si. Зменшити перехідні опори контактів Al / Si можна за допомогою тонких буферних шарів незбідненого ПК. Фізична основа ефекту зменшення питомого перехідного опору пов'язана із збільшенням ефективної площі контакту, в результаті чого перехідні опори контактів Al / Si можуть бути зменшені на порядок.

Лекція 7. Оптичні властивості нанокомпозитів на основі поруватого кремнію. Багатошарові поруваті структури. Створення світловодних елементів. Інтерференційний фільтр Фабрі–Перо. Фотонні кристали.

Як ви знаєте,нанокомпозитні середовища є тією базою, на якій створюються нові матеріали із заданими структурними, електронними та оптичними властивостями, які визначаються розміром, формою і впорядкованістю складових їх наночастинок, а також факторами заповнення наночастинками. Серед різноманітних наноструктурованих середовищ слід особливо відзначити пористі напівпровідники і діелектрики, утворені шляхом видалення з об'єму частини матеріалу, представником яких є поруватий кремній. Виникаючі при цьому пори і нанокристали, що залишаються, мають розміри від одиниць до сотень нанометрів. Фізичні властивості одержаних структур відрізняються від властивостей вихідного матеріалу, часто радикально. Яскравим прикладом суттєвих змін при переході від об'ємного до наностуктурованого стану кремнію є розглянута нами раніше видима ФЛ ПК. Можна виділити три основні причини модифікації властивостей:

1 ) квантоворозмірні ефекти для нанооб'єктів, розміри яких є співмірними з довжиною хвилі де Бройля електрона;

2 ) поверхневі ефекти, пов'язані з появою нових електронних і фононних станів поверхні, площа якої помітно (іноді на кілька порядків) збільшується після утворення пор;

3 ) локальні поля в нанокомпозитному середовищі, що визначаються розмірами, формою і впорядкованістю нанооб'єктів.

Простота методики отримання і можливість керувати властивостями пористих напівпровідників, змінюючи режим формування, роблять їх досить зручними об'єктами для створення нових фотонних середовищ. До числа важливих властивостей пористих напівпровідників відносяться менші, ніж в об'ємних матеріалах, показник заломлення і діелектрична проникність, що може виявитися корисним як для створення різних оптичних покриттів, так і для вирішення завдання формування середовищ з низькою діелектричною проникністю, досить актуальною у світлі зменшення розмірів компонентів в комп'ютерній індустрії. Дуже важливі для практичних застосувань і вельми розвинена поверхня пористих середовищ, і можливість їх заповнення різними газами і діелектричними рідинами, що дозволяє використовувати такі середовища в якості сенсорів.

Особливої уваги заслуговують такі нанокомпозитні середовища, в яких нанооб'єкт розташовані більш-менш впорядковано і/або характеризуються анізотропної формою. Останній фактор є основною причиною виникнення оптичної анізотропії і, зокрема, подвійного променезаломлення форми в таких середовищах.

У тому випадку, коли характерні розміри пор і нанокристалів багато менше довжини хвилі випромінювання, наноструктуровані напівпровідники можна розглядати як однорідне оптичне середовище, що має деякий ефективний показник заломлення, відмінний від показників заломлення речовин, що утворюють наноструктуру (так звана модель ефективного середовища) [6]. Вибираючи параметри обробки, можливо в широких межах керувати структурними (пористість, розмір і форма пор і нанокристалів) властивостями пористих напівпровідників і, як наслідок, їх оптичними параметрами (показником заломлення, величинами подвійного променезаломлення і дихроїзма), а також товщиною формованих пористих шарів, щоб створити необхідні оптичні середовища та пристрої, включаючи фотонні кристали.

7.1. Моделі ефективного середовища. Дуже важливу роль в оптиці нанокомпозитних середовищ відіграє так звана модель ефективного середовища. Суть цієї моделі полягає в тому, що ансамбль нанокластеров можна розглядати як якусь нову середу з ефективною діелектричної проникністю. Очевидною перевагою даного підходу є те, що в його рамках для аналізу поширення випромінювання в нанокомпозитному середовищі немає необхідності розв'язувати рівняння Максвелла в кожній точці простору. Як правило, в моделі ефективного середовища для оптичних задач користуються електростатичним наближенням, умовою якого є малість як розміру наночастинок, так і відстані між ними в порівнянні з довжиною оптичної хвилі в середовищі. В іншому випадку неминуче постає завдання врахування розсіяння на частинках, з яких складається нанокомпозитне середовище, і інтерференції розсіяних хвиль. У рамках моделі ефективного середовища знаючи оптичні параметри кожного з компонентів композитної середовища, а також їх концентрацію і геометричну форму, ми в принципі можемо визначити ефективні параметри всієї середовища як цілого. Для цього треба зв'язати електричну індукцію ‹D›, усереднену за об'ємом (V), розміри якого набагато перевищують розміри неоднорідностей діелектричної проникності,

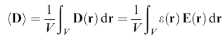(1)

і величину напруженості зовнішнього електричного поля Е_о. Тут D(r), Е(r) і (ε) - локальні ( в точці з радіус - вектором r) значення електричної індукції, напруженості електричного поля і діелектричної проникності. Цей зв'язок і визначає ефективну діелектричну проникність ε_eff композитної середовища:

(2)

Локальне поле Е(r) залежить від форми частинки. У самому загальному випадку інтегрування у формулі (1) зустрічає значні труднощі. Точне визначення ε_eff можливо в декількох виключних випадках, наприклад у випадку ламінарної структури, що складається з паралельних шарів діелектриків з проникностями ε₁ та ε₂,що чергуються. Для інших завдань доводиться розглядати різні наближення, беручи до уваги локальні поля, які визначають з рішення задач електростатики. Одними з найбільш широко застосовуваних моделей ефективного середовища є моделі Максвелла - Гарнета [13] і Бруггемана [ 14 ], що обумовлено насамперед їх фізичною наочністю.

7.1. Моделі ізотропної ефективного середовища Локальне поле в кулі. Моделі ізотропного ефекного середовища Максвелла - Гарнета і Бруггемана базуються на вирішенні задачі електростатики про локальне поле в кулі. Розглянемо кулю з діелектричної проникностю ε₁, яка оточена діелектричним середовищем з проникністю ε₂. Локальне поле Е₁ всередині кулі складається із зовнішнього поля Е_о і поля поляризованої сфери (поля Лоренца ) 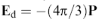, напрямок якого залежить від співвідношення величин ε₁ та ε₂

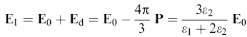(3)

де

- вектор поляризації середовища в кулі, а χ_о - величина поляризуємості сфери.

Модель Максвелла - Гарнета. Тепер розглянемо об'єм V, утворений середовищем з проникністю ε₂ з рідкими сферичними включеннями з діелектричної проникністю ε₁. Поляризація даного об'єму складається з поляризацій кожного зі сферичних включень:

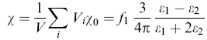(4)

де V - об'єм r –ої частинки, а 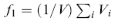- об'ємний фактор заповнення. Даний об'єм буде характеризуватися ефективною діелектричної проникністю ε_eff. Якщо цей об'єм має форму кулі і оточений середовищем з діелектричної проникністю ε₂, то полярізуємість такого об'єму відповідно до (3) дорівнюватиме

(5)

З (4 ) і ( 5 ) випливає формула Максвелла - Гарнета

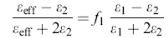(6)

Як видно, компоненти композитного середовища нерівноправні. Прийнято вважати, що модель Максвелла - Гарнета справедлива, коли один матеріал є матрицією, а другий утворює в ній ізольовані включення, причому об'ємна частка останніх невелика (так звані матричні середовища).

Модель Бруггемана. У тому випадку, коли в композитному середовищі не можна виділити матрицю і включення (так зване статистичне середовище), часто користуються моделлю, запропонованою Бруггеманом. Розглянемо середовище, утворене кулями з двох матеріалів. У даній моделі вважається, що кожна частка поміщена не в середовище матриці, а в деяке ефективне середовище з ефективною діелектричної проникністю ε_eff, що відрізняється від діелектричної проникності ε₁, ε₂ кожного з компонентів. Крім того, робиться припущення, що на кожну кулю діє поле, яке є усередненим по всьому об'єму. Таким чином, середнє поле ‹Е› визначається полями Е₁ і Е₂, існуючими в кулях з ε₁ та ε₂ відповідно: , де f₁ та f₂ - відповідні фактори заповнення (f₁+f₂=f). Враховуючи зв'язок ‹Е›, Е₁ і Е₂, який дається формулою (3), отримуємо

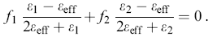(7)

У даному випадку два компоненти, що формують нанокомпозитне середовище, рівноправні. Умовою застосовності даної моделі є обмеження на фактори заповнення, обумовлене вимогою контакту між нанокластерами (перколяційні межі ):

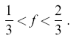(8)

Крім зазначених двох моделей широке застосування знаходить модель Бергмана, згідно якої

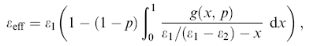(9)

де р - пористість, а g {х, р) - функція спектральної густини, яка не залежить від властивостей матеріалів, що утворюють нанокомпозит, а визначається виключно геометрією. У даному запису підінтегральний вираз з точністю до коефіцієнта являє собою фактор локального поля з фактором деполяризації х. В результаті аналізу оптичних властивостей пористого кремнію на основі моделей ефективного середовища було показано, що для мезопористого кремнію невеликої пористості хороші результати дає застосування моделі Бруггемана. Для мікропористого кремнію, розміри нанокристалів в якому складають одиниці нанометрів, застосування цієї моделі вимагає врахування квантово- розмірного ефекту.

Врахування анізотропії форми в моделях ефективного середовища. Звернемо увагу на те, що в анізотропному середовищі діелектрична проникність залежить від напрямку електричного поля. Ми маємо справу з анізотропією, зумовленої структурою системи і формою компонентів, що утворюють композитну середу. Таку анізотропію прийнято називати анізотропією форми.

Локальне поле в еліпсоїді. Моделі ефективного середовища Максвелла - Гарнета і Бруггемана допускають своє узагальнення на випадок анізотропії форми складових часток середовища. Нехай, наприклад, середовище містить рідкі включення у формі еліпсоїдів (модель Максвелла - Гарнета) або складається з таких еліпсоїдів (модель Бруггемана). Нам знову потрібно звернутися до вирішення завдання електростатики, на цей раз до задачі про локальне поле в еліпсоїді. Як і у випадку кулі, поляризація діелектрика зменшує поле всередині еліпсоїда. Поле Е₁ всередині діелектрика складається із зовнішнього поля Е_о і деполяризующего поля Е_д. Компоненти поля всередині еліпсоїда виявляються наступними

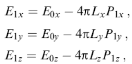(10)

де L - фактор деполяризації. Таким чином, для однорідного зовнішнього прикладеного поля результуюче поле всередині еліпсоїда буде також однорідним, хоча воно і не обов'язково буде збігатися за напрямком з зовнішнім полем. Величину L можна визначити, розв'язавши рівняння Лапласа в еліптичних координатах. Різним головним осях відповідають різні величини L; три фактори деполяризації для трьох головних осей еліпсоїда (х, у і z) пов'язані між собою співвідношенням

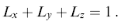(11)

Узагальнення моделей Максвелла - Гарнета і Бруггемана на випадок анізотропії. Для моделі Максвелла - Гарнета розглянемо включення у формі еліпсоїдів. Тоді модифікована формула буде мати вигляд

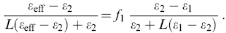(12)

У моделі Бруггемана слід вважати, що в середовищі з ефективною діелектричної проникністю знаходяться еліпсоїди з матеріалів з ε₁ та ε₂. Узагальнена формула Бруггемана набуде вигляду

(13)

Різними напрямками поля будуть відповідати різні фактори деполяризації і, як наслідок, різні величини ефективної діелектричної проникності, що дозволяє врахувати анізотропію за допомогою моделі ефективного середовища. Відзначимо, що для наночастинок сферичної форми (L = 1/3) формули ( 12 ) і ( 13 ) перейдуть в (6 ) і ( 7 ) відповідно.

7.2. Подвійне променезаломлення пористого кремнію. Кремній має гратку високої симетрії типу алмаза (симетрія m3m) і, як наслідок, мале подвійне променезаломлення. У кристалічного кремнію максимальна величина подвійного променезаломлення спостерігається для світлової хвилі, що розповсюджується вздовж кристалографічного напрямку [110], і становить Δn= n_‹110› - n_‹100› =5х10^-6. Оскільки електрохімічне травлення сильнолегованого кристалічного кремнію з дірковим типом провідності (р⁺⁺-Sі) характеризується переважним зростанням пор вздовж кристалографічних осей (100) (рис. 7.1), то симетрія пористого шару знижується в порівнянні з кристалічним кремнієм, що проявляється у виникненні так званого "подвійного променезаломлення форми". Для шарів ПК, отриманих на підкладці з орієнтацією поверхні (100), оптична вісь спрямована вздовж кристалографічного напрямку [100], а подвійне променезаломлення стає помітним тільки при падінні випромінювання на поверхню зразка під кутом до нормалі. У разі використання пластин з низькою симетрією поверхні, наприклад ( 110 ) і ( 211 ), шари мезопористого кремнію мають властивості одноосного кристала, у якого оптична вісь лежить у площині поверхні.

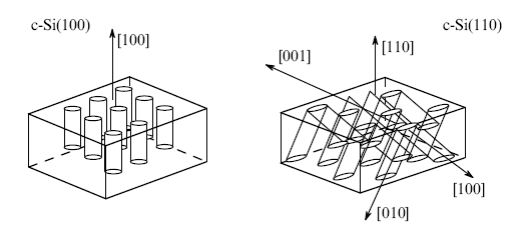
Рис. 7.1. Схематичне зображення розташування пор в ПК, отриманому на пластинах з орієнтацією поверхні (100) і (110).

Відомо, що подвійне променезаломлення в багатьох середовищах може бути викликано виникненням напруг. Однак рентгенівський аналіз нанокристалів ПК свідчить про збереження в ПК структури типу алмазу. Оцінки, засновані на пружньооптичних константах, показують, що подвійного променезаломлення викликане спотворенням кристалічної решітки в даному випадку мізерне, тобто кожен кремнієвий нанокристал є оптично ізотропним. Таким чином, спостерігається ефект обумовлений виключно анізотропією форми пор і нанокристалів. Сформовані таким чином шари ПК мають властивості негативного одновісного кристала (рис. 7.2), при цьому оптична вісь ПК, виготовленого на підкладці р⁺⁺-Sі з орієнтацією поверхні (110), лежить у площині поверхні і збігається з кристаллографічним напрямком [001].

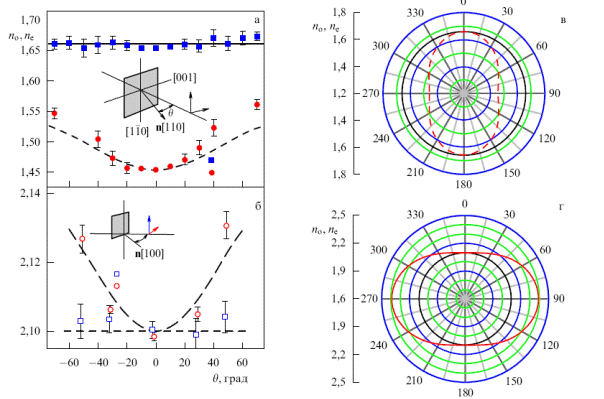
Рис. 7.2. Залежності показників заломлення в ІЧ діапазоні від кута падіння випромінювання на плівку (а, б) і від кута між оптичною віссю і напрямком хвильового вектора в шарі (в, г) для ПК, отриманого на підкладках з орієнтаціями (110) (а, в) і (100) (б, г). □, ■ і суцільні криві відповідають звичайній хвилі, o, ● і штрихові криві - незвичайній хвилі.

Дійсно, при обертанні зразка навколо осі [ 110 ] для випромінювання, поляризованого параллельно цій осі, показник заломлення практично не змінюється, як це і повинно бути для звичайної хвилі. Навпаки, для випромінювання, поляризованого в одній площині з віссю [ 001 ], показник заломлення залежить від кута падіння на зразок. Залежність показника заломлення для незвичайної хвилі від кута в між оптичною віссю і напрямком хвильового вектора дається формулою

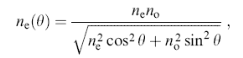(14)

де кут θ пов'язаний з кутом падіння випромінювання на зразок θ_о як

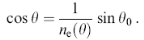(15)

Як видно з рис. 7.2а, дійсно спостерігається узгодженість експериментальних даних і результатів розрахунків за формулами (14) і (15). Відмінність показника заломлення від розрахункового пояснюється розбіжністю (непаралельністю) пучка ІЧ випромінювання на відстані, співрозмірній з розміром зразка і з неоднорідністю самого зразка. Величина подвійного променезаломлення істотно залежить від пористості, значення якої визначається у тому числі й густиною струму травлення.

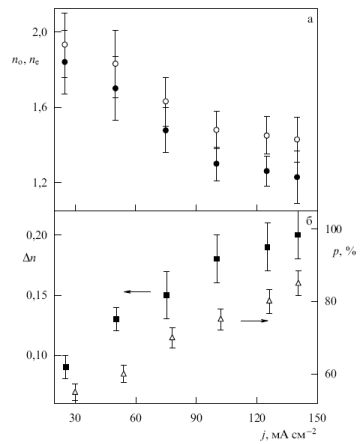
Рис. 7.3. Залежності ( а ) показників заломлення для звичайної і незвичайної хвиль (o та ● відповідно), (б) величини подвійного променезаломлення ( ■ ), а також пористості (Δ ) від густини струму травлення.

Як видно з рис. 7.3, збільшення пористості супроводжується зменшенням ефективних показників заломлення для звичайної і незвичайної хвиль і зростанням величини подвійного променезаломлення Δn= n_о - n_e, яка для високопористих шарів досягала 0,24 в ІЧ області при середній величині показника заломлення (n_o + n_e) /2 = 1,3. Відзначимо, що це значення Δn перевищує аналогічну величину для ісландського шпату (Δn = 0,15).

Тип подвійного променезаломлення і розташування оптичної осі залежать від морфології пористого шару, яка визначається рівнем легування вихідного кристалічного кремнію, орієнтацією його поверхні і густиною струму травлення. Використання кристалічного кремнію з тією ж орієнтацією поверхні (110), але з меншим рівнем легування (р⁺-Sі, 20-100 мОм см) призводить до того, що в даному випадку оптична вісь, хоча і лежить в площині поверхні, збігається з кристалографічним напрямком [110]. Така структура також проявляє властивості негативного кристала. Цікаво відзначити, що на відміну від випадку р⁺⁺-Sі, із зростанням густини струму травлення і пористості величина подвійного променезаломлення зменшується. Дані ефекти викликані менш упорядкованим розташуванням пор в ПК, отриманому на основі р⁺-Sі.

У шарах ПК, виготовлених на підкладці з орієнтацією поверхні ( 100 ), пори розташовуються по нормалі до поверхні (див. рис. 7.1 ). Це обумовлює позитивний тип подвійного променезаломлення в таких шарах. Залежність показників заломлення для звичайної і незвичайної хвиль для ПК, сформованого на підкладці орієнтації ( 100 ) з питомим опором 15 мОм см від кута падіння випромінювання на зразок наведена на рис. 7.2в. Дійсно, дана плівка ПК проявляє властивості позитивного кристала, як це і передбачається теорією.

Варто також відзначити, що величиною подвійного променезаломлення можна управляти, заповнюючи пори діелектричними рідинами. Зокрема, ця ідея використовувалася для детектування конденсації рідин в порах.

Дисперсія оптичних параметрів і моделювання оптичної анізотропії в пористому кремнії. Використовуючи узагальнену модель Бруггемана, можна розрахувати показники заломлення ПК. При цьому ПК розглядається як ансамбль еліпсоїдів обертання, осі яких спрямовані паралельно; напрямок осей обертання еліпсоїдів збігається з оптичною віссю. Вибір даної моделі виправданий реальною формою кремнієвих нанокристалів, що спостерігалася за допомогою електронної та атомно -силової мікроскопії. У розрахунку для визначення діелектричної проникності кристалічного кремнію використовувалася відома залежність його показника заломлення від довжини хвилі. У таких розрахунках величини факторів деполяризації і пористості грають роль підгінних параметрів.

Дихроїзм в пористому кремнії. Вимірювання коефіцієнта поглинання ПК в діапазоні 0,54-0,82 мкм в плівках, виготовлених на пластинах р⁺⁺-Sі з орієнтацією ( 110 ), показали, що для випромінювання, поляризованого вздовж кристалографічного напрямку [ 110 ], ця величина вище ніж для випромінювання, поляризованого вздовж [ 001 ]. Із зменшенням довжини хвилі величина дихроїзма Δκ= Im n_о- Im n_e зростає ( рис. 7.4). Цей факт також добре описується запропонованою вище моделлю (експериментальні дані і результати розрахунку для довжин хвиль понад 0,6 мкм). Однак для довжин хвиль менше 0,52 мкм величина Δκ падає зі зменшенням довжини хвилі. Така немонотонна залежність від довжини хвилі пов'язана з виходом з меж застосування статичного наближення ефективного середовища і частковою деполяризацією випромінювання, що проходить через плівку ПК, викликаною розсіюванням на

Рис.7.4. Дисперсія величини дихроїзму в (110) ПК, пористість 74%. Суцільна лінія - результат розрахунку по узагальненої моделі Бруггемана.

наночастинках. Дійсно, в кремнії довжина світлової хвилі, відповідна 0,5 мкм у вакуумі, становить близько 0,15 мкм, що є співмірним з розміром нанокристалів і пор в мезопористому кремнії ( 0,02-0,05 мкм).