Расчет на прочность червячных передач

Червячные передачи, аналогично зубчатым, рассчитывают на контактную прочность и на изгиб зубьев червячного колеса как менее прочных по сравнению с витками червяка.

Как отмечалось выше в червячных передачах кроме выкрашивания рабочих поверхностей зубьев велика опасность заедания и износа, которые зависят от величины контактных напряжений 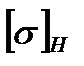. Поэтому, в отличие от зубчатых, для всех червячных передач расчет по контактным напряжениям является основным, а расчет по напряжениям изгиба — проверочным.

Расчет по контактным напряжениям. В основу вывода расчетных формул для червячных передач положены те же исходные зависимости и предположения, что и в зубчатых передачах (см. с. 106).

Наибольшее контактное напряжение в зоне зацепления по формуле Герца

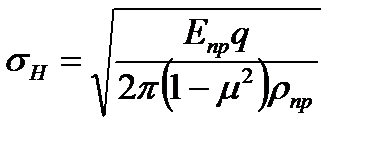
где E_np — приведенный модуль упругости; E_np = 2E₁E_i/(E₁ + E₂)

Для стального червяка E_np = 210 МПа; для бронзового или чугунного колеса E_np = 98 МПа;

μ — коэффициент Пуассона. Для стали, бронзы и чугуна μ 0,3;

q — нормальная нагрузка на единицу длины контактных линий. Эта нагрузка распределяется неравномерно вследствие деформаций валов червяка и колеса, а также подшипников и корпуса передачи;

q =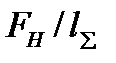

F_Н — нагрузка, нормальная к поверхности зуба червячного колеса и витка червяка и приложенная в полюсе зацепления. Согласно рис. 5.12, а

F_Н = F_a1/(cos a cos Y) — F_t2/(cos a cos Y) = 2T₂/(d₂ cos a cos Y);

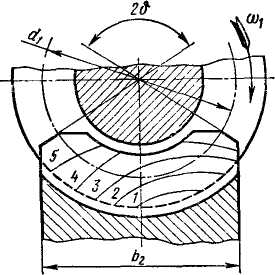
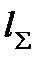— суммарная длина контактных линий в зацеплении червячной передачи. Согласно рис. 5.13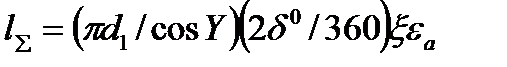

Коэффициент 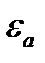= 0,75 учитывает уменьшение длины контактной линии в связи с тем, что соприкосновение витка с зубом осуществляется не по полной дуге обхвата с углом 2 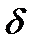, а так, как показано на рис. 5.13.

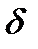
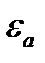При угле обхвата 2 100° и коэффициенте торцового перекрытия в средней плоскости сечения колеса = 1,8—2,2, длина контактных линий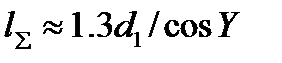

По аналогии с косозубой зубчатой передачей

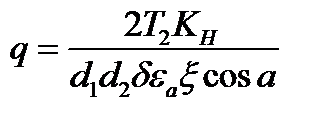
После подстановки и преобразований получим

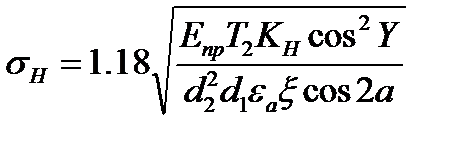(5.31)

Здесь дополнительно введен К_Н — коэффициент нагрузки, учитывающий неравномерность распределения нагрузки вследствие деформации деталей передачи, а также дополнительные динамические нагрузки,

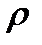_пр — приведенный радиус кривизны профилей витков червяка и зубьев колеса в полюсе зацепления.

В осевом сечении профиль витка червяка прямолинейный (см. рис. 5.8), поэтому приведенный радиус кривизны для червячной пары равен радиусу кривизны профиля зуба червячного колеса в полюсе зацепления .

Учитывая, что межосевое расстояние 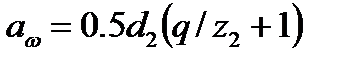, решаем формулу (5.31) относительно межосевого расстояния

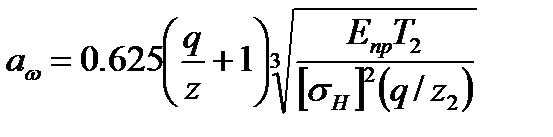. (5.32)

Червячные передачи работают плавно, бесшумно, поэтому в них дополнительные динамические нагрузки невелики. Хорошая приработка зубьев колес к виткам червяков значительно уменьшает концентрацию нагрузки.

При удовлетворительной точности изготовления принимают: К_Н = 1 — при постоянной нагрузке и v₂ 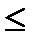3 м/с, : К_Н = 1,1—1,4 — при переменной нагрузке и v₂ > 3 м/с.

Расчет по напряжениям изгиба. Расчет зубьев червячного колеса на изгиб аналогичен расчету зубьев цилиндрических косозубых колес. Вследствие дугообразной формы зубьев (см. рис. 5.10) считают, что их прочность на изгиб примерно на 40% выше, чем зубьев цилиндрических косозубых колес.

Особенности формы зубьев червячного колеса учтены в табл. 5.6.

Таблица 5.6. Коэффициенты формы зуба червячных колес Y_F2

20 24 26 28 30 32 35 37 40 45 50 60 80 100 150 300 YF2 1,98 1,88 1,85 1,80 1,76 1,71 1,64 1,61 1,55 1,48 1,45 1,40 1,34 1,30 1,27 1,24

При среднем значении делительного угла подъема линии витка 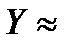10° коэффициент

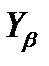= 1 — Y/140° = 1—10^o/140" = 0,93 и т_n = т cos Y = 0,98 т.

С учетом этих поправок получается формула проверочного расчета червячных передач по напряжениям изгиба:

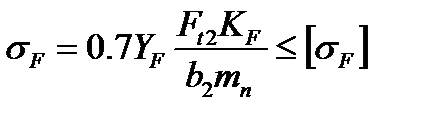(5.33)

где 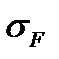— расчетное напряжение изгиба в опасном сечении зубьев червячного колеса; 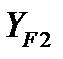— коэффициент формы зуба колеса, который выбирают по табл. 5.6 в зависимости от эквивалентного числа зубьев

Так как зуб червячного колеса имеет угол наклона у, то по аналогии с косозубым колесом

Z_v2 = z₂/cos³Y. (5.34)