Тема 1.2.1. Измерение количества информации

Алфавитный подход используется для измерения количества информации в тексте, представленном в виде последовательности символов некоторого алфавита. Такой подход не связан с содержанием текста. Количество информации в этом случае называется информационным объемом текста, который пропорционален размеру текста — количеству символов, составляющих текст. Иногда данный подход к измерению информации называют объемным подходом.

Каждый символ текста несет определенное количество информации. Его называют информационным весом символа. Поэтому информационный объем текста равен сумме информационных весов всех символов, составляющих текст.

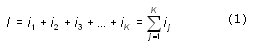
Здесь предполагается, что текст — это последовательная цепочка пронумерованных символов. В формуле (1) i₁обозначает информационный вес первого символа текста, i₂—информационный вес второго символа текста и т.д.; K —размер текста, т.е. полное число символов в тексте.

Все множество различных символов, используемых для записи текстов, называется алфавитом. Размер алфавита — целое число, которое называется мощностью алфавита. Следует иметь в виду, что в алфавит входят не только буквы определенного языка, но все другие символы, которые могут использоваться в тексте: цифры, знаки препинания, различные скобки, пробел и пр.

Определение информационных весов символов может происходить в двух приближениях:

1) в предположении равной вероятности (одинаковой частоты встречаемости) любого символа в тексте;

2) с учетом разной вероятности (разной частоты встречаемости) различных символов в тексте.

Приближение равной вероятности символов в тексте

Если допустить, что все символы алфавита в любом тексте появляются с одинаковой частотой, то информационный вес всех символов будет одинаковым. Пусть N — мощность алфавита. Тогда доля любого символа в тексте составляет 1/N-ю часть текста. По определению вероятности эта величина равна вероятности появления символа в каждой позиции текста:

p = 1/N

Согласно формуле К.Шеннона, количество информации, которое несет символ, вычисляется следующим образом:

i = log2(1/p) = log2N (бит)(2)

Следовательно, информационный вес символа (i) и мощность алфавита (N) связаны между собой по формуле 2ⁱ = N.

Зная информационный вес одного символа (i) и размер текста, выраженный количеством символов (K), можно вычислить информационный объем текста по формуле:

I = K i (3)

Эта формула есть частный вариант формулы (1), в случае, когда все символы имеют одинаковый информационный вес.

Из формулы (2) следует, что при N = 2 (двоичный алфавит) информационный вес одного символа равен 1 биту.

С позиции алфавитного подхода к измерению информации 1 бит— это информационный вес символа из двоичного алфавита.

Более крупной единицей измерения информации является байт.

1 байт— это информационный вес символа из алфавита мощностью 256.

Поскольку 256 = 2⁸, то из формулы Хартли следует связь между битом и байтом:

2ⁱ = 256 = 2⁸

Отсюда: i = 8 бит = 1 байт

Для представления текстов, хранимых и обрабатываемых в компьютере, чаще всего используется алфавит мощностью 256 символов. Следовательно,
1 символ такого текста “весит” 1 байт.

Помимо бита и байта, для измерения информации применяются и более крупные единицы:

1 Кб (килобайт) = 2¹⁰ байт = 1024 байта,

1 Мб (мегабайт) = 2¹⁰ Кб = 1024 Кб,

1 Гб (гигабайт) = 2¹⁰ Мб = 1024 Мб.