Получение когерентных волн в оптике.
Метод деления амплитуды волны
3.1. 1.ОБЩИЕ ПОЛОЖЕНИЯ.В однородных средах волны распространяются прямолинейно. При наличии неоднородностей возникают отклонения от прямолинейности.
Дифракцией называют совокупность волновых явлений наблюдаемых при распространении света в среде с резкими неоднородностями, и связанных с отклонениями от законов геометрической оптики (границы непрозрачных или прозрачных тел, малые отверстия).
Дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Опыт Юнга с интерференцией от двух щелей обеспечил прочную основу волновой теории света. Однако общее признание волновая теория получила лишь благодаря детальному изучению дифракции более чем через десятилетие. Фундаментальный смысл дифракции состоит в том, что она ограничивает возможности концентрации света в пространстве, кладет предел разрешающей способности оптических и спектральных приборов, влияет на формирование оптического изображения и т. п.
 |
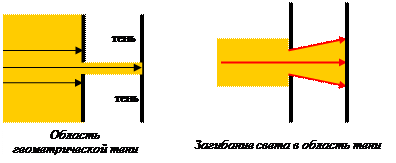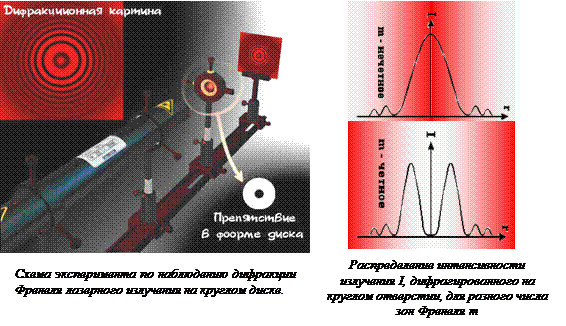
Пусть, например, непрозрачный экран с круглым отверстием освещается параллельным пучком света. Варианты описания процессов взаимодействия света с веществом не однозначны. Мы можем увидеть:
а) равномерно освещенное круглое пятно с резкой границей света и тени, в точности повторяющее размеры и форму отверстия (геометрическая оптика);
б) граница света и тени становится размытой, а внутри пятна возникают чередующиеся светлые и темные кольца (дифракция Френеля);
в) размер освещенного пятна становится сущес-твенно больше размеров отверстия (дифракция Фраунгофера).
Итак, нам нужен рецепт, который позволял бы описывать законы распространения волн, отличные от законов геометрической оптики.
3.1.2. ПРИНЦИП ГЮЙГЕНСА—ФРЕНЕЛЯ. МЕТОД ЗОН ФРЕНЕЛЯ.Для расчета и объяснения дифракционных явлений применяется принцип Гюйгенса–Френеля. С помощью принципа Гюйгенса можно объяснить проникновение световых волн в область геометрической тени. Но он не дает сведений об амплитуде и интенсивности волн. Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн. Принцип Гюйгенса-Френеля является рецептом для расчета дифракционных задач, обладающих определенной симметрией. Рассмотрим точечный источник S в изотропной однородной среде. Определим интенсивность света в центре дифракционной картины (точка Р). Источник S и точка наблюдения Р расположены на оси отверстия.
 |
Окружим S волновой поверхностью G, каждый элемент которой является источником вторичных волн. Далее заменим реальный источник света S вспомогательной поверхностью G, которая содержит всю информацию об источнике. Расстояние от источника S до вершины волновой поверхности равно а, а от вершины до точки Р – b. Разобьем из точки Р волновую поверхность G на участки (зоны) так, что расстояния от краев каждой зоны до точки Р отличаются на l / 2:
b + l / 2; b + 2l / 2; b + 3l / 2; b + 4l / 2; …, b + ml / 2,
где m – число зон Френеля. Центральная зона представляет шаровой сегмент, а остальные – шаровые пояса.
Свойства зон Френеля:
· Фазы колебаний, приходящие в точку Р от двух соседних зон, отличаются на p: С учетом этого результирующее колебание, создаваемое всеми зонами запишется так:
·
 |
При не слишком больших m площади зон Френеля s примерно одинаковы:
·
 |
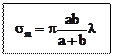
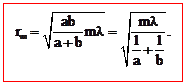Легко показать, радиус m-й зоны для сферических волн определяется выражением:
· Для плоской волны а®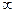 
и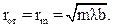 
Радиусы зон rm зависят от расстояния a между источником и препятствием, от расстояния b между точкой наблюдения и препятствием, от длины волны λ.
· 
Амплитуды Еm зон монотонно убывают с ростом их номера m:
Разобьем все нечетные зоны пополам и найдем результирующую амплитуду:
 |
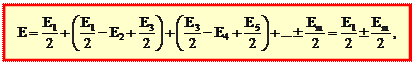где учтено, что все скобки равны нулю. Знак плюс соответствует нечетным m, минус – четным.
Рассмотрим частные случаи прохождения волн через различные препятствия.
 |
Открытый волновой фронт(нет препятствия)
Для открытого волнового фронта
Еm = Е 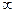® 0 и Е = Е1 /2,
т. е. свет в отсутствии препятствия распространяется внутри канала размером в половину первой зоны Френеля. Размер первой зоны Френеля для плоской волны имеет величину порядка r1 =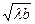 
» 0,7 ×10-3 м. Обратите внимание на удивительный факт: амплитуда колебаний в точке наблюдения в отсутствии препятствия на пути волны вдвое меньше, чем амплитуда Е1 колебания, созданного отверстием в одну зону Френеля, а интенсивность вчетверо меньше. 
Дата добавления: 2015-12-26; просмотров: 729;