Критерий, основанный на известных вероятностных состояниях «природы».

Если известны вероятности состояний «природы» (например, спроса по данным анализа за прошлые годы):

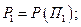
где 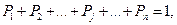то в качестве показателя эффективности (рациональности, обоснованности) стратегии берется средний (математическое ожидание) - выигрыш применения этой стратегии:

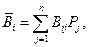
а оптимальной считают стратегию, для которой этот показатель эффективности имеет максимальное значение, т.е.

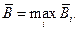
Если каждому решению соответствует множество возможных результатов 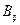с вероятностями 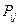, то среднее значение выигрыша определяется по формуле

а оптимальная стратегия выбирается по условию

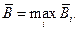
В этом случае можно воспользоваться и стратегией минимального среднего риска для каждого i-го состояния «природы»

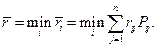
Максиминный критерий Вальдапредполагает выбор решения, при котором гарантируется максимальный выигрыш в наихудших условиях внешней среды (состояния «природы»):

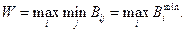
Согласно критерию пессимизма-оптимизма Гурвицапри выборе решения вместо двух крайностей в оценке ситуации (оптимум-пессимизм) придерживаются некоторого компромисса, учитывающего возможность как наихудшего, так и наилучшего поведения «природы»:

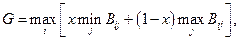
где x - показатель пессимизма-оптимизма (чаще всего 0,5).

Если 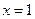критерий слишком пессимистичный, если 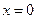– слишком отптимистичный.

По критерию минимаксного риска Сэвиджавыбирают ту стратегию, при которой величина риска имеет минимальное значение в самой неблагоприятной ситуации:

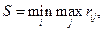
чтобы избежать слишком большого риска при выборе решения.

Комплексный анализ всех этих критериев позволяет в некоторой мере оценить возможные последствия принимаемых решений