Динамические характеристики измерительных систем
При анализе динамических погрешностей каждое звено измерительной системы и систему в целом следует рассматривать как динамическую систему. Способы описания таких систем излагаются в курсе теории автоматического управления (ТАУ). Ограничимся одним, но наиболее часто используемым случаем, когда измерительную систему можно рассматривать как линейную динамическую систему. Тогда измерительное звено может быть описано следующими динамическими характеристиками.
1). Дифференциальное уравнение звена – линейное с постоянными коэффициентами 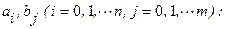
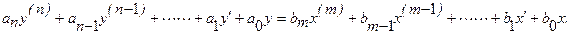
В статическом режиме работы все производные равны нулю и поэтому
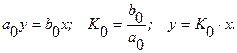
Дифференциальное уравнение, однако, не очень удобный инструмент анализа сложных структур. Поэтому обычно от сигналов как функций времени переходят к из отображению по Фурье или Лапласу.
2). Передаточная функция звена. Для ее получения преобразуем обе части дифференциального уравнения по Лапласу при нулевых начальных условиях:
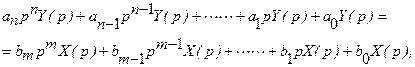
где:
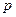 - переменная Лапласа,
- переменная Лапласа,
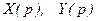 - отображения по Лапласу для входного и выходного сигналов данного измерительного звена.
- отображения по Лапласу для входного и выходного сигналов данного измерительного звена.
Полученное соотношение позволяет найти отношение изображений выходного и входного сигналов:
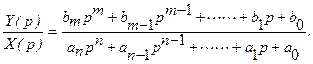
По аналогии со статической чувствительностью это отношение называется операторной чувствительностью или передаточной функцией звена
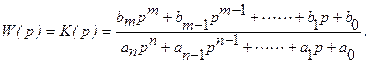
Эта характеристика более компактна для записи и поэтому каждое  - ое системы можно теперь представить так, как это изображено на рисунке
- ое системы можно теперь представить так, как это изображено на рисунке
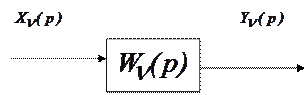 |
Теперь мы можем считать, что по каналам связи передаются лапласовы отображения сигналов, а звенья системы по отношению к ним ведут себя как статические блоки с чувствительностями  равными передаточным функциям. От передаточной функции всегда можно перейти к дифференциальному уравнению, используя процедуру, обратную ранее изложенной.
равными передаточным функциям. От передаточной функции всегда можно перейти к дифференциальному уравнению, используя процедуру, обратную ранее изложенной.
3). Амплитудно-фазовая частотная характеристика звена (АФЧХ) получается аналогично передаточной функции после преобразования по Фурье обеих частей дифференциального уравнения звена, то есть заменой 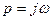 в выражении для передаточной функции:
в выражении для передаточной функции:
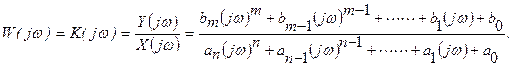
АФЧХ представляет собой комплексное выражение:
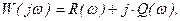
где 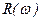 действительная часть АФЧХ или действительная частотная характеристика (ДЧХ),
действительная часть АФЧХ или действительная частотная характеристика (ДЧХ),
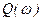 мнимая часть АФЧХ или мнимая частотная характеристика.
мнимая часть АФЧХ или мнимая частотная характеристика.
Модуль АФЧХ
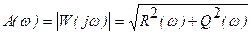
называется амплитудно-фазовой частотной характеристикой (АЧХ) и представляет собой зависимость отношения амплитуды выходного сигнала к амплитуде входного синусоидального сигнала от его частоты.
Аргумент АФЧХ
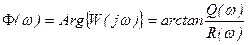
называется фазово-частотной характеристикой и представляет собой зависимость сдвига фазы выходного сигнала по отношению к фазе входного синусоидального сигнала от его частоты.
Поэтому, если на вход измерительного звена или измерительной системы подается синусоидальный сигнал с амплитудой 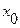 и частотой
и частотой 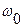
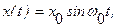
то сигнал на его выходе будет также гармоническим, но зависящим от значений его АФЧХ (или АЧХ и ФЧХ) на частоте 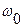 входного сигнала:
входного сигнала:
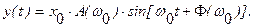
4). Переходная функция звена определяется как реакция звена 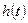 на единичное воздействие на его входе. Если
на единичное воздействие на его входе. Если 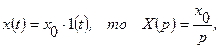 поэтому изображение выходного сигнала
поэтому изображение выходного сигнала
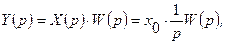
а оригинал имеет вид:
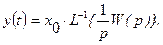
Переходная функция
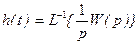
характеризует быстроту и особенности процесса затухания переходных процессов в звене.
5). Импульсная (весовая) функция определяется как реакция звена 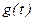 на δ-импульс, приложенный ко входу звена в момент t=0. Если
на δ-импульс, приложенный ко входу звена в момент t=0. Если 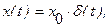 то
то 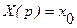 и изображение выходного сигнала
и изображение выходного сигнала
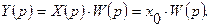
Поэтому выходной сигнал
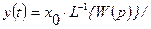
Импульсная (весовая) функция
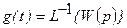
позволяет определить выходной сигнал при любой форме входного сигнала с помощью интеграла свертки входного сигнала и импульсной функции:
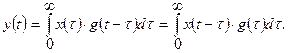
Кроме перечисленных динамических характеристик в обиходе широко используется несколько упрощенных характеристик.
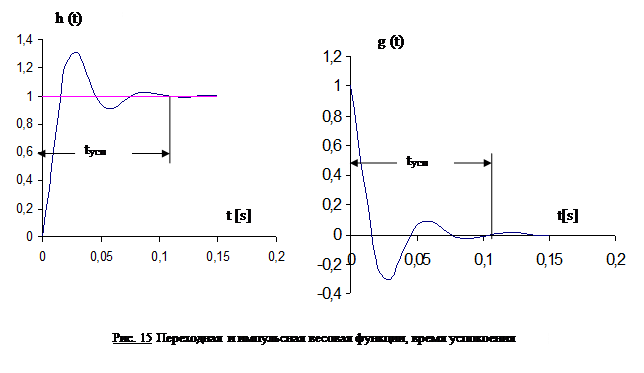
6). Время успокоения 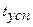 - это промежуток времени (рис. 15), необходимый для затухания импульсной или переходной функции
- это промежуток времени (рис. 15), необходимый для затухания импульсной или переходной функции
 |
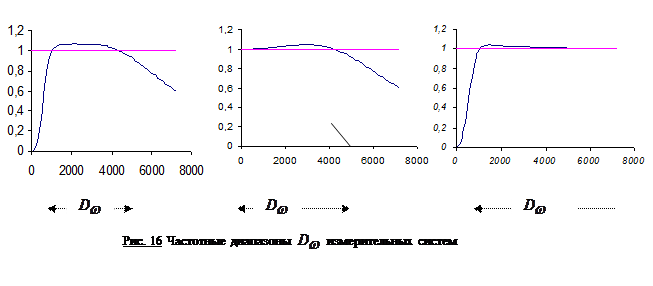



 7). Частотный диапазон измерительного звена или системы – это интервал частот, ограниченный граничными частотами
7). Частотный диапазон измерительного звена или системы – это интервал частот, ограниченный граничными частотами 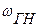 и
и 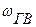 , в пределах которого АЧХ остается практически постоянной, то есть чувствительность одинакова к гармоникам любой частоты.
, в пределах которого АЧХ остается практически постоянной, то есть чувствительность одинакова к гармоникам любой частоты.
| |||||||
 | |||||||
 | 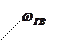 | ||||||
Предполагается, что ФЧХ в пределах частотного диапазона также остается постоянной или изменяется линейно с частотой. В последнем случае все гармонические составляющие сигнала и, следовательно, сам сигнал просто сдвигается по времени на определенную величину 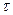 .
.
Дата добавления: 2015-11-28; просмотров: 1181;