Погрешность измерительной системы

Измерительная система – это некоторая система, состоящая из отдельных звеньев, связанных друг с другом каналами связи.

Предположим, что номинальные ФП всех звеньев линейны. Тогда суммарная чувствительность всей системы является некоторой функцией чувствительности отдельных звеньев:

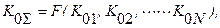
где N число звеньев.

Условимся обозначать через 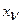входной сигнал для 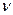-того эвена и через 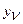- его выходной сигнал. Тогда, при последовательном соединении звеньев, выходной сигнал 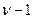-го звена 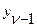будет равен входному сигналу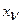 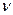-того звена. Входной сигнал первого звена 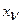будем обозначать просто через 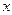и выходной сигнал последнего звена 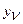- просто через .

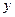Суммарную погрешность каждого звена можно трактовать, как погрешность его чувствительности. Действительно, для некоторого 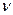-того эвена имеем:

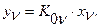
С учетом погрешности 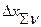следует записать

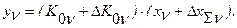
где 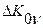- погрешность чувствительности v-того звена, действующая аналогично погрешности 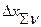. Сравнивая это равенство с предыдущим, получим (пренебрегая произведением ):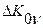

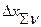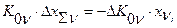
и поэтому

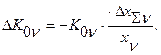
Погрешность чувствительности системы складывается ив погрешностей чувствительностей отдельных звеньев в соответствии с равенством:

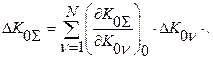
Это равенство можно записать в виде:

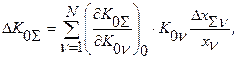
поэтому

.

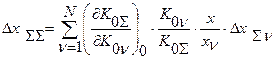Выражения:

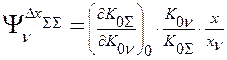
являются коэффициентами влияния погрешности 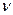-того звена на суммарную погрешность системы, поэтому

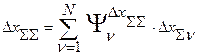
Полученное выражение позволит теперь по погрешностям отдельных звеньев найти суммарную погрешность измерительной системы. Речь здесь идет однако о сложении погрешностей конкретных экземпляров звеньев в результирующую погрешность конкретного экземпляра измерительной системы.

При определении вероятностных характеристик суммарной погрешности для ансамбля измерительных систем данного типа необходимо учитывать то обстоятельство, что внешние воздействия одновременно влияют на работу всех или многих звеньев системы. Поэтому соответствующие составляющие эксплуатационной погрешности могут быть сильно коррелированны.

Если система собрана в одном месте и внешние воздействия оказывают одинаковое влияние на все её элементы, то эксплуатационную погрешность желательно вообще выделить из суммарной погрешности. Тогда получаем

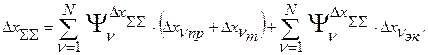
Но

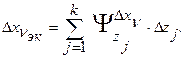
Поэтому

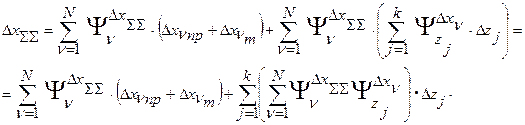
Произведение под знаком последней суммы - это коэффициенты влияния внешних воздействий на суммарную погрешность 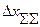. Обозначим их через .

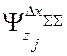Теперь все слагаемые второй суммы стали независимыми случайными величинами и можно приступить к определению вероятностных характеристик погрешности:

- математическое ожидание

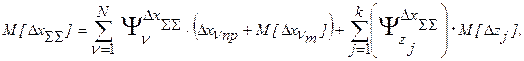
- дисперсия суммарной погрешности

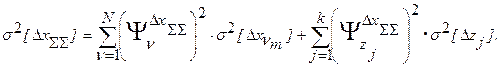
Далее, аналогично предыдущему, можно найти и зону погрешностей в соответствии с выражением:

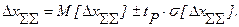
Коэффициенты влияния погрешностей отдельных звеньев находятся из структурной схемы соединения звеньев в систему.

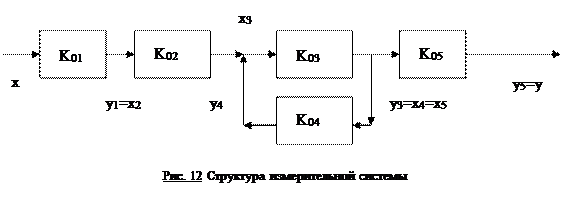
Пример. Структура системы изображена на рис.12.

Суммарная чувствительность:

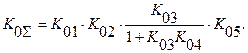
Поэтому коэффициент влияния выходной погрешности, например, 4-го звена на суммарную выходную погрешность будет иметь вид:

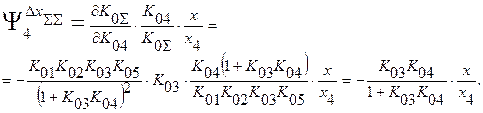
Выразим теперь 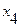через

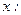
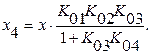
Поэтому окончательно имеем:

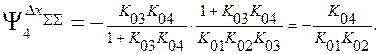
Аналогично этому можно найти и коэффициенты влияния других звеньев ни суммарную погрешность.

Коэффициенты влияния можно найти и по-другому, путем соответствующей перестройки структуры системы. Для этого необходимо:

- входной сигнал положить равным нулю;

- перестроить структуру так, чтобы погрешность 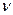-того звена стала входной величиной для новой структуры;

- последним звеном новой структуры сделать фиктивное звено с чувствительностью 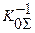, обратной суммарной чувствительности системы.

- чувствительность новой системы равна теперь коэффициенту влияния данного звена.

Так при определении коэффициента влияния 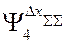в изображенной выше структуре преобразованная структура должна иметь вид. представленный на рис. 13.

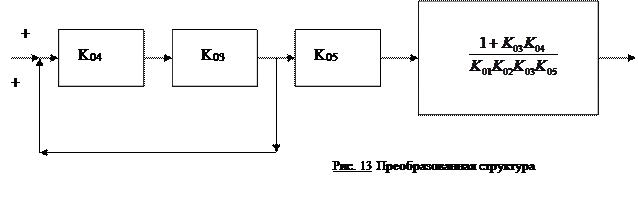
Здесь чувствительность 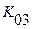третьего звена вынесена со знаком минус, поскольку в исходной структуре сигнал с выхода 1-го звена подается на вход 3-го звена с отрицательным знаком. В соответствии с этой новой структурой

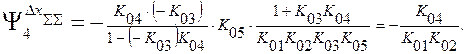
Это - тот же результат, что и найденный выше. Аналогично можно найти и остальные коэффициенты влияния. Соединяя в суммарную схему все преобразованные структуры, необходимые для отслеживания коэффициентов влияния всех звеньев, можно построить единую структуру, отображающую механизм образования суммарной погрешности измерительной системы.

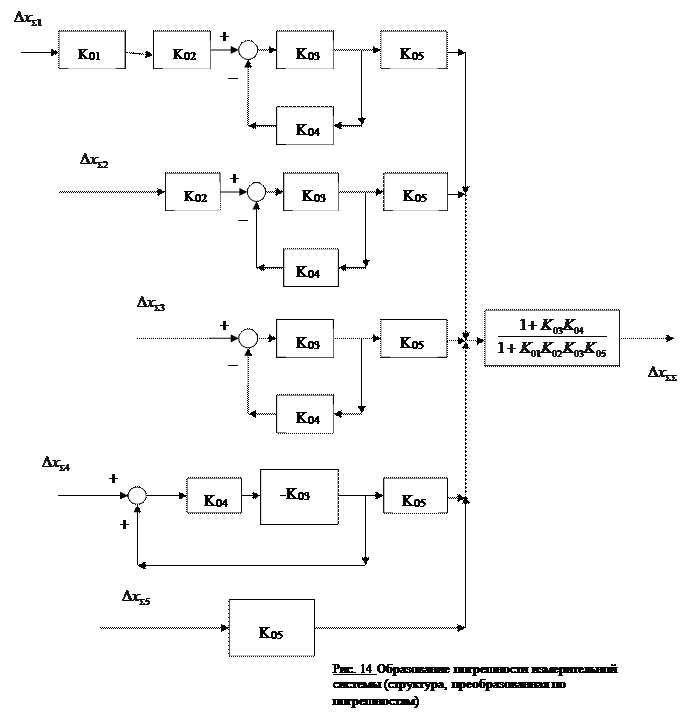
Для системы, рассматриваемой в данном примере, получаем структуру, изображенную на рис. 1.14.

Следует, однако, помнить, что эта преобразованная структура отображает механизм преобразования только лишь суммы погрешности приближения и технологической погрешности каждого звена и не учитывает механизм образования эксплуатационной погрешности.