Равномерное приближение
Отличается использованием аппарата полиномов Чебышева, наименее отклоняющихся от нуля в диапазоне [-1; +1] среди всех других полиномов той же степени. Соберем в таблицу несколько первых полиномов Чебышева степени n=1, 2, …., 5.
| n | Полином Чебышева
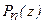
| Наибольшее отклонение
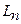
| Точки наибольших отклонений
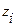
| Корни
полинома
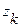
|
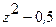
| 0,5000 | 0; ±1 | ±0,7071 | |
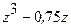
| 0,2500 | ±0,5; ±I | 0; ±0,866 | |
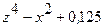
| 0,1250 | 0; ±0,7071; ±1 | ±0,3827; ±0,9239 | |
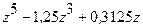
| 0,0625 | ±0,309; ±0б809; ±1 | 0; ±0,5878; ±0.9511 |
Графически эти полиномы выглядят следующим образом (рис. 1.5).
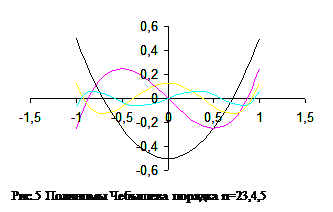
Возможны две методики приближения.
I) Функцию преобразования 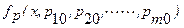 можно разложить в степенной ряд Тейлора в середине
можно разложить в степенной ряд Тейлора в середине 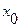 диапазона преобразования
диапазона преобразования 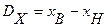 :
:
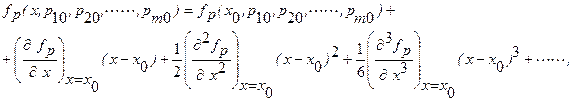
где 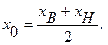
Делаем замену переменных:
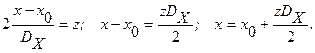
Поскольку 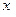 изменяется в пределах от
изменяется в пределах от 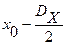 до
до 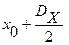 , то переменная
, то переменная 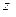 будет теперь изменяться в диапазоне [-1; +1].
будет теперь изменяться в диапазоне [-1; +1].
В результате получаем:
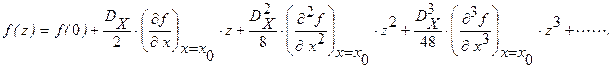
Погрешность приближения при линейной номинальной функции преобразования
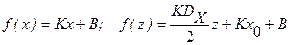
составляет
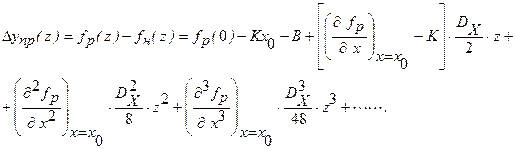
Таким образом, мы представили погрешность приближения в форме полинома от переменной 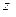 в диапазоне ее изменения от –1 до +1. Всегда, уже по внешнему виду функция преобразования, можно судить о том, какой степенью этого полинома можно ограничиться. Во всяком случае, при предварительном анализе можно ограничиться степенью
в диапазоне ее изменения от –1 до +1. Всегда, уже по внешнему виду функция преобразования, можно судить о том, какой степенью этого полинома можно ограничиться. Во всяком случае, при предварительном анализе можно ограничиться степенью 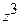 и затем уточнить решение.
и затем уточнить решение.
Ограничиваясь третьим членом разложения, приведем выражение для 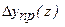 к форме, сопоставимой с полиномами Чебышева. Для этого вынесем коэффициент
к форме, сопоставимой с полиномами Чебышева. Для этого вынесем коэффициент 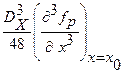 за скобки:
за скобки:
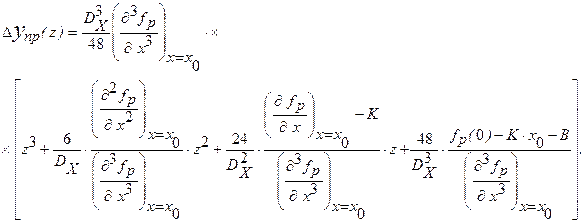
Для того, чтобы стоящей в квадратных скобках полином был действительно полиномом Чебышева, необходимо выполнение следующих условий:
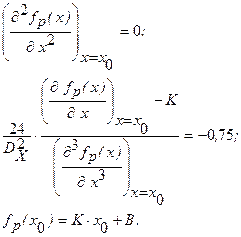
Исходя из этих условий, можно теперь выбирать расчетные значения ВП, входящих в выражение для ФП. Наибольшее значение погрешности схемы получается при этом равным:
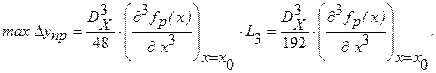
Пример. Синусный механизм обладает расчетной функцией преобразования
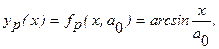
которая раскладывается в степенной ряд относительно точки 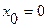 следующим образом:
следующим образом:
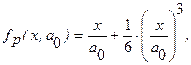
поскольку
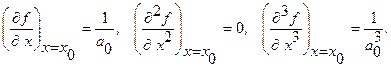
Пусть функция преобразования должна иметь вид:
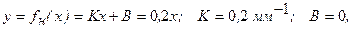
а диапазон преобразования 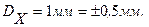
Первое и третье условия выполняются автоматически. Второе условие приводит к выражению
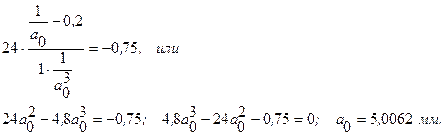
Полученное решение и является искомым значением расчетного параметра, то есть плеча синусного рычага. Это решение получено из условия равномерного приближения ФП синусного механизма к линейной ФП (в диапазоне ±0,5 мм).
Наибольшее значение погрешности приближения составляет:
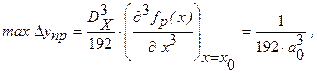
или в единицах входной величины
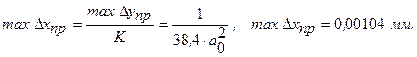
2) Вторая методика приближения не требует предварительного разложения функция преобразования в степенной ряд и основывается на использовании корней полинома Чебышева.
Если решен вопрос о выборе степени аппроксимирующего полинома Чебышева, то погрешность схемы должна обратиться в нуль в точках диапазона, соответствующих корням полинома Чебышева. Поэтому расчетные значения внутренних параметров можно найти из соотношений:
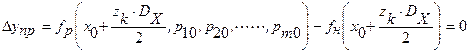
при всех 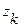 (
( 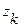 - корни полинома).
- корни полинома).
Пример: Для синусного механизма
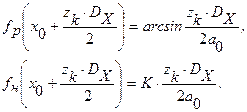
Поэтому параметр 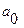 можно найти из условия равенства значений расчетной и номинальной функций преобразования при
можно найти из условия равенства значений расчетной и номинальной функций преобразования при 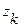 =±0,866:
=±0,866:
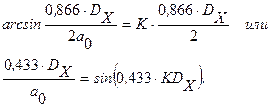
Поэтому
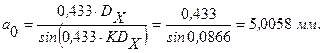
Погрешность приближение составляет при этом:
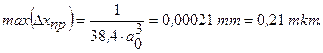
Дата добавления: 2015-11-28; просмотров: 961;
