Приближение в среднем квадратическом

Здесь минимизируется дисперсия погрешности приближения

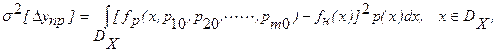
Поэтому для определения расчетных значений внутренних параметров можно непосредственно использовать выражение:

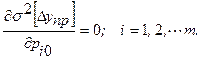
Существуют стандартные программы минимизации подобных функционалов, поэтому решение задачи, если оно существует, всегда может быть найдено.

Пример. Синусный механизм при тех же данных при равномерной плотности распределения значений измеряемой величины в диапазоне преобразования :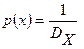

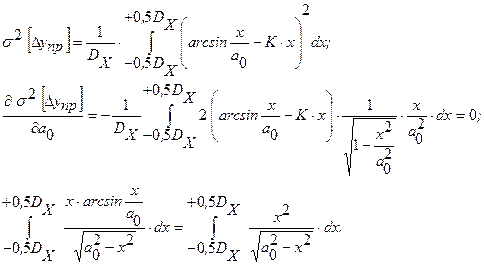
После интегрирования получаем:

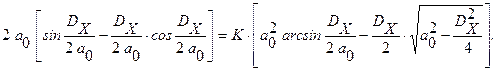
Решение такого уравнения возможно опять таки только численными методами, так что лучше сразу же численно минимизировать выше написанный интеграл.

Для определения расчетных значений ВП можно также использовать способ, аналогичный равномерному приближения полиномами Чебышева.

Для этих целей используются полиномы Лежандра, отличающиеся тем, что среди всех полиномов денной степени они имеют .наименьшее среднее квадратическое отклонение от нуля. Первые пять полиномов Лежандра имеют вид:

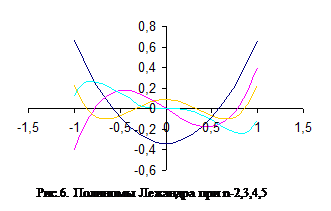
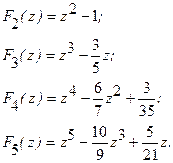
Ход определения расчетных значений внутренних параметров при использовании полиномов Лежандра тот же, что и при использовании полиномов Чебышева.