Трифазна мережа, що живить кілька симетричних навантажень

В розгалуженій мережі позначимо активні та реактивні потужності споживачів, відповідно, p_k і q_k , а потужності на ділянках мережі P_k і Q_k. Складаємо їх послідовно для кожної ділянки, враховуючи навантаження (рис.7.5).

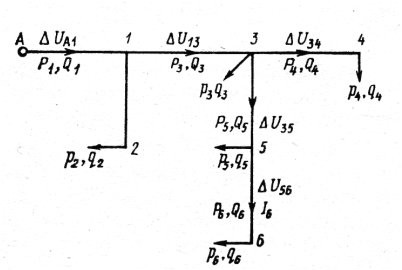
Рисунок 7.5. Схема розгалуженої мережі

Втрата напруги до найбільш віддаленої точки 4 визначається за допомогою формули ( ) як сума втрат напруг на ділянках від джерела живлення до розглядуваної точки:

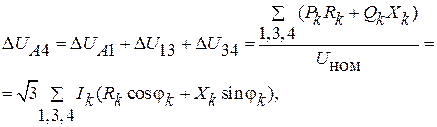
а поперечна складова

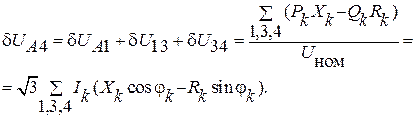
У формулах ( ), ( ) 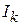, 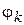- модуль і фаза струму на розглядуваній ділянці мережі

; ;

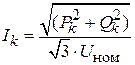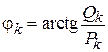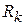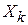, - активний та індуктивний опори ділянок мережі. Якщо позначити суму опорів ділянок від 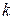-го навантаження до джерела живлення і , то формули ( ) і ( ) можна перетворити до вигляду:

; ( )

. ( )

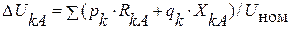Формули ( )–( ) дозволяють обчислити і втрату напруги магістралі (рис.7.6).

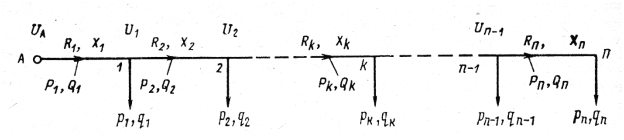
Рисунок 7.6. Магістраль, що живить декілька навантажень

Якщо магістраль однорідна і на всьому протязі має однакову площу перерізу, формулу ( ) можна записати у вигляді

. ( )

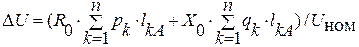В останньому випадку втрата напруги визначається «моментом» навантаження.

Якщо втрати напруги обчислюють, виходячи з потужності на ділянках ліні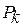ї і 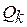, у формулу ( ) необхідно підставляти опори цих же ділянок 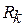та 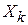. Якщо ж розрахунок виконують, виходячи з активних та реактивних навантажень споживачів 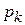і 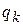, то у відповідності з формулою ( ) треба застосовувати опори ліній і від її початку до точки приєднання розглядуваних навантажень.

У ряді випадків при проектуванні мереж (наприклад, живлячих зовнішнє освітлювальне навантаження міст і селищ) застосовують рівномірний розподіл навантаження по довжині лінії (рис.7.7).

Позначимо потужність на одиницю довжини лінії 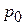. Втрата напруги в лінії з активним рівномірно розподіленим навантаженням

. ( )

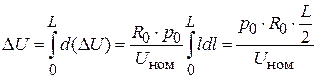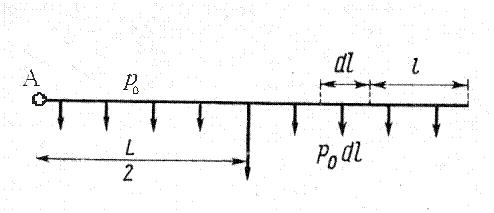
Рисунок 7.7. Лінія з рівномірно розподіленим навантаженням

При обчисленні втрати напруги навантаження, що рівномірно розподілене по всій довжині лінії, його можна замінити зосередженим, що прикладене до її середини.