Тема 11. Методические основы прогнозирования в принятии логистических решений.

Принципы прогнозирования развития логистических систем.

Повышение адаптивности логистических систем.

Динамический ряд, тренд и прогнозная тенденция.

Метод корреляционно-регрессионного анализа и метод сценариев при обосновании логистических решений.

Принципы прогнозирования развития логистических систем.

Прогнозирование– процесс получения прогностической информации. Прогноз:

1) вероятностное представление о появлении событий в будущем, основанное на наблюдениях и теоретических положениях;

2) обоснованное суждение о вероятности наступления одного или нескольких событий или о возможных состояниях процесса (явления);

3) суждение о будущем периоде времени.

Процедура прогнозирования:

1) определение объектов прогноза;

2) отбор объектов, которые прогнозируются;

3) определение временных горизонтов прогноза – краткосрочный прогноз, среднесрочный или долгосрочный;

4) отбор модели (моделей) прогнозирования;

5) сбор данных, необходимых для прогноза;

6) обоснование модели прогнозирования;

7) составление прогноза;

8) отслеживание результатов.

Методы прогнозирования– это различные способы определения вероятного развития события на заданном отрезке времени в будущем и установления его объемов в денежном или натуральном выражении.

Они разрабатываются, как правило, для специфических целей использования, поэтому невозможно дать полный обзор всех существующих методов.
Обычно используются стандартные методы, имеющие сложную структуру. Методы прогнозирования могут основываться, в частности, на репрезентативном опросе и опросе экспертов.

Всю совокупность методов можно разделить на следующие
основные группы:

1) логико-экономические методы – прогноз составляется в форме логических оценок и суждений на основе всестороннего анализа тенденций его развития в прошлом и на современном этапе (к моменту составления прогноза) с учетом ожидаемых изменений социально-экономических условий и факторов (изменение цен, рост численности населения, перестройка ассортимента, выход на рынок новых товаров). Прогноз носит характер экспертной оценки. Проведение экспертных оценок осуществляется по специальной процедуре, и ни в коем случае нельзя полагаться на мнение одного специалиста, каким бы опытным и квалифицированным он ни был;

2) экономико-математические методы – базируются на применении приемов математической статистики. Наиболее часто применяемым является метод экономико-математического моделирования. В этом случае прогноз составляется на основе реализации модели, которая представляет собой некую систему числовых показателей, связанных между собой таким образом, что они воспроизводят основные связи и закономерности изучаемого явления;

3) нормативные методы – основаны на использовании системы норм и нормативов рационального потребления. При этом подходе за ориентир принимается норма рационального потребления конкретного вида товаров на некоторую перспективу.

Повышение адаптивности логистических систем.

В соответствии с современной теорией, одной из основных функций системы управления предприятием принято считать рациональное регулирование параметров ключевых бизнес-процессов и координирование деятельности входящих в него подразделений. Бизнес-процессы при этом рассматриваются как строго упорядоченные последовательности действий (операций) над идеальными и/или материальными объектами, выполняемые при определенных условиях [1].

К основным видам бизнес-процессов, характерным для промышленных предприятий, можно отнести следующие:

- разработка стратегий;

- разработка новых видов продукции;

- совершенствование и модификация выпускаемой продукции;

- реорганизация производственно-технической базы;

- налаживание и развитие двусторонних связей предприятия с внешней средой;

- реализация заказов.

Под адаптивным управлением обычно понимается управление с обратной связью, отличающееся от обычного наличием специального адаптивного (приспособительного) механизма. Этот механизм накапливает и анализирует информацию о прошлых управленческих ситуациях, вырабатывает новое поведение на основе прошлого опыта. При этом основным ориентиром являются заложенные в систему управления цели и критерии, т.е. используются прогностические значения параметров, описывающих ситуацию [3].

В качестве такого механизма при управлении социально-экономическими системами используется модель управляемого объекта. С помощью модели осуществляется прогноз возможного развития ситуации при выборе той или иной стратегии управляющего воздействия. Предсказуемое поведение управляемого объекта возможно лишь при построении модели объекта, адекватно отображающей среду функционирования и сам объект управления.

Структура адаптивной системы управления показана на рисунке 1.

Рисунок 1 - Структура адаптивной системы управления

Адаптивная система управления производством организационно состоит из двух взаимосвязанных систем: адаптивной системы планирования и адаптивной системы регулирования. Структурно эти две системы практически идентичны [2].

Функциональная каждая из них состоит из следующих взаимосвязанных частей:

- модели планирования (соответственно регулирования);

- имитационной модели функционирования системы;

- внутреннего (имитационного) адаптера;

- внешнего (объектного) адаптера.

В адаптивной системе планирования, основываясь на полученных параметрах, по модели планирования определяют план и потенциальный эффект. План рассматривается как траектория, заданная последовательностью плановых состояний, распределенных во времени. По имитационной модели осуществляется имитация реализации плана, и оцениваются потери, не позволяющие достичь потенциального эффекта. Имитация реализации плана выполняется несколько раз для получения статистически значимых оценок показателей плана. По результатам расчета плана и имитации его выполнения проводятся оценка и анализ приемлемости плана. Если план с учетом его возможной реализации приемлем, то он принимается к исполнению. В противном случае внутренний адаптер, основываясь на результатах имитации, подстраивает параметры модели планирования и модели регулирования, и работа схемы повторяется, начиная с пересчета плана при новых параметрах. Работа внутреннего адаптера базируется на одном из методов оптимизации в условиях помех.

В соответствии с самой природой конкуренции, лидеры рынка последних лет будут сменены конкурентоспособными фирмами. Это можно продемонстрировать в контексте концепции стройности и адаптивности.

Как адаптивность, так и стройность предъявляют требования высокого качества продукта. Они также требуют минимизации общего времени удовлетворения потребности, которое определяется как время от подачи заявки клиентом до доставки товара. Общее время исполнения должно быть минимизировано для обеспечения адаптивности, поскольку спрос сильно вариативен и трудно предсказуем. Если цепь имеет долгие периоды доставки, то она не может достаточно быстро реагировать на потребности, чтобы завоевывать рынок. К тому же, эффективное реструктурирование сокращения операционных циклов всегда приводит к хорошей основе для сокращения производственных затрат и повышения производительности.

Сроки исполнения необходимо сократить в стройном производстве путем отношения к затратам времени именно как к затратам, а стройность предполагает устранение всех затрат. Суть разницы между стройностью и адаптивностью в отношении обеспечения добавления стоимости для покупателя в том, что уровень обслуживания (доступность) критичный показатель для адаптивности, в то время как затраты и следовательно низкая продажная цена тесно связана со стройностью. Тем не менее, там, где концепция сокращения общего времени цикла, при эффективном внедрении, является достаточным условием достижения стройного производства, это лишь одно из условий достижения адаптивного снабжения.

Методы стройности могут являться полезным фактором адаптивности предприятия. В частности, где волны спроса могут быть разделены и/или где концепция разгруппировочной точки может использоваться, существует реальная возможность использования гибридных стратегий. Существует также одна важная причина, почему стройность предшествует адаптивности. Реальное и эффективное изменение требует расписывания и понимания всех бизнес процессов.

Для повышения эффективности функционирования отраслей и предприятий необходимо тщательно анализировать и периодически осуществлять реинжиниринг бизнес-процессов, включая построение новых схем адаптивности [3].

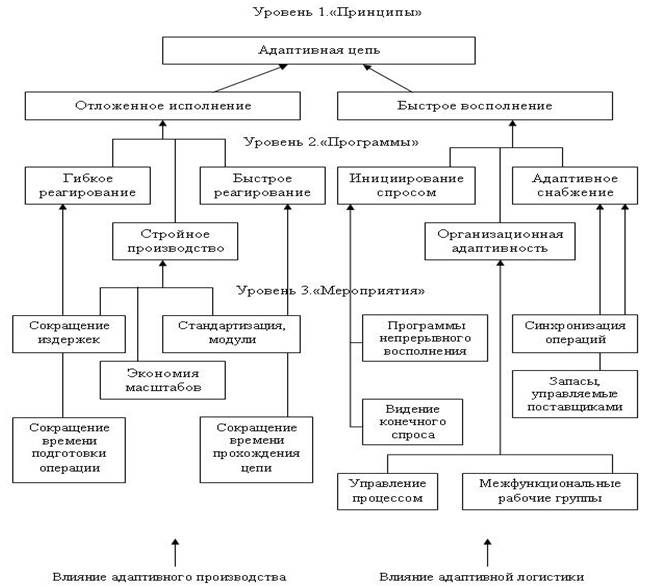
Рисунок 2- Интегральная модель для внедрения адаптивной цепи

На уровне 1 выделены ключевые принципы адаптивной цепи, быстрого товарного восполнения и откладывания исполнения конкретной потребности. На уровне 2 установлены конкретные программы, такие как стройное производство, организационная адаптивность, и быстрое реагирование, которые должны быть внедрены для достижения принципов уровня 1. Уровень 3 определяет отдельные действия, которые необходимо предпринять для поддержки уровня 2, например сокращение времени, насыщение и улучшение качества информации, и устранение всех излишних элементов, вызывающих издержки. Не все из перечисленных характеристик могут быть использованы в любом маркетинговом или производственном контексте, но вероятно, что адаптивная логистическая цепь охватывает многие из этих элементов.

Таким образом, внедрение адаптивных систем в схемы бизнес-процессов могут существенным образом повысить эффективность их реализации.

Литература

1. Юревич Е.И. Теория автоматического управления. - СПб.: БXВ-Петербург, 2007.

2. Жданов А.А.. Метод автономного адаптивного управления// Известия Академии наук. Теория системы управления, 1999. -№ 5.

3. Срагович В.Г. Адаптивное управление. – М.: Наука, 1981.

Динамический ряд, тренд и прогнозная тенденция.

Группировка первичного материала и вычисление обобщающих показателей позволяют на этапе статистического исследования решать задачи анализа развития изучаемых явлений, во-первых, во времени и, во-вторых, во взаимосвязи.

Первая задача решается путем построения и обработки динамических (временных) рядов, которые представляют собой совокупности последовательно расположенных показателей, характеризующих изменение какого-либо явления во времени.

При изучении временных рядов ставятся следующие цели: краткое описание характерных особенностей ряда; подбор статистических моделей, описывающих временной ряд; предсказание будущих значений на основе прошлых наблюдений; управление процессом, порождающим временной ряд.

На практике эти и подобные цели достижимы далеко не всегда и далеко не в полной мере. Этому, препятствует, во-первых, недостаточный объем наблюдений и, во-вторых, изменяющаяся с течением времени статистическая структура временного ряда. Из-за этих факторов значение прошлых наблюдений обесце­нивается, и они уже не помогают предвидеть будущее.

При практическом анализе временных рядов последовательно проходятся следующие этапы: графическое представление и описание поведения временного ряда; выделение и удаление закономерных составляющих временного ряда, зависящих от времени: тренда, сезонных и циклических составляющих; выделение и удаление низко- или высокочастотных составляющих процесса; исследование случайной составляющей временного ряда, оставшейся после удаления перечисленных выше составляющих; построение математической модели для описания случайной составляющей; прогнозирование будущего развития процесса, представленного временным рядом; исследование взаимодействий между различными временными рядами. С учетом необходимости решения указанных выше задач исследователями используется большое количество методов: сглаживание и фильтрация - для преобразования временных рядов с целью удаления из них высокочастотных или сезонных колебаний; модели скользящего среднего и регрессии - для описания и прогнозирования процессов, проявляющих однородные колебания вокруг среднего значения;

экстраполяция и прогнозирование - для предсказания будущих значений временного ряда на основе подобранной модели поведения; корреляционный анализ - для выявления существенных зависимостей и их лагов внутри одного процесса или между несколькими процессами; спектральный анализ - для нахождения периодических и квазипериодических составляющих временного ряда.

Построение динамического ряда является простым и наглядным приемом отображения изменения какого-либо явления во времени. В одних случаях построение ряда без дополнительной обработки выявляет тенденцию развития явления. Но бывают случаи, когда тенденция развития явно не просматривается, так как показатели ряда колеблются. В этом случае для выявления тенденций требуется определенная аналитическая обработка динамического ряда.

При анализе временного ряда его видимую изменчивость стараются разделить на закономерную и случайную составляющие. Закономерные изменения членов временного ряда следуют определенному правилу и поэтому предсказуемы. Эта составляющая Уt может быть вычислена при каждом t как некоторая функция от текущего момента t, причем эта функция может зависеть от некоторого набора параметров. Когда параметры неизвестны, их приходится оценивать по имеющимся наблюдениям - так бывает в случае использования регрессии.

Изменчивость, оставшаяся необъяснимой, иррегулярна и хаотична. Для ее описания необходим статистический подход.

Под закономерной {детерминированной) составляющей Уt временного ряда У1, У2, ..., Уn понимается числовая последовательность D1, D2, ..., Dn, элементы которой Dt вычисляются по определенному правилу как функция времени t.

Детерминированная составляющая отражает действие каких-либо определенных причин или факторов. Для рядов в криминологии и социальных науках причины, порождающие закономерные составляющие, могут быть неочевидными. Тем не менее, их сово­купное влияние может быть устойчивым в течение достаточно длительных промежутков времени. Это обеспечивает возможность прогноза для временных рядов.

Если удается полностью выявить закономерную составляющую в поведении временного ряда, то оставшаяся часть выглядит хаотично и непредсказуемо. Ее обычно называют случайным компонентом и обозначают

Формы разложения временного ряда на детерминированный и случайный компоненты могут различаться.

Аддитивной моделью временного ряда называется представление ряда в виде суммы детерминированного и случайного компонентов:

Мультипликативной моделью временного ряда называется представление ряда в виде произведения детерминированного и случайного компонентов:

При переходе к логарифмам в мультипликативной модели вновь получаем аддитивную модель, но уже для логарифмов .

Способы описания детерминированных компонентов временного ряда зависят от области приложений.

В детерминированном компоненте временного ряда, обычно выделяют три составляющие: тренд TRt, сезонный компонент St и циклический компонент Сt. При этом термины «тренд», «сезонный компонент» и «циклический компонент» не имеют однозначных общепринятых определений.

Анализ временного ряда обычно начинается с выделения компонента, называемого в правовой статистике, трендом: его присутствие или отсутствие наглядно показывает график временного ряда.

Трендом временного ряда TRt, при t=1, ..., n называют плавно изменяющийся, не циклический компонент, описывающий чистое влияние долговременных факторов, эффект которых сказывается постепенно.

Сезонный компонент отражает повторяемость процессов во времени.

Сезонный компонент St временного ряда при t = 1, ..., n описы­вает поведение, изменяющееся регулярно в течение заданного пе­риода (года, месяца, недели, дня и т.п.). Он состоит из последова­тельности почти повторяющихся циклов.

Сезонные эффекты присущи многим сферам человеческой активности: многие виды продукции имеют сезонный характер про­изводства, некоторые виды преступлений (кражи, изнасилования) также имеют ярко выраженную сезонность.

Сезонный компонент может иметь плавающий, или изменяющийся характер. Идея подхода к анализу сезонных компонентов заключается в переходе к сравнению значений через определенный период времени. Так, при изучении динамики месячных количеств краж за несколько лет данные декабря одного года обычно сравнивают с данными декабря предыдущего года.

Циклический компонент занимает промежуточное положение между закономерной и случайной составляющими временного ряда. Если тренд - это плавные изменения, проявляющиеся на больших временных промежутках, если сезонный компонент - это периодическая функция времени, ясно видимая, когда ее период много меньше общего времени наблюдений, то под циклическим компонентом обычно подразумевают изменения временного ряда, достаточно плавные и заметные для того, чтобы не включать их в случайную составляющую, и которые нельзя отнести ни к тренду, ни к сезонному, периодическому компоненту.

Циклический компонент Сt, временного ряда описывает длительные периоды относительного подъема и спада. Он состоит из циклов, которые меняются по амплитуде и протяженности.

Числовые значения показателей динамического ряда называются уровнями ряда, которые могут быть выражены абсолютными показателями, относительными и средними величинами.

В тех случаях, когда уровни выражены абсолютными показателями, различают интервальные и моментные ряды.

Интервальным называется такой ряд, абсолютные уровни которого характеризуют величину изучаемого явления, полученную в итоге за определенный период времени.

Моментным называется ряд, абсолютные уровни которого характеризуют величину явления по состоянию на определенные моменты времени.

Таким образом, в интервальном ряду интервал - это промежу­ток времени, за который обобщены приводимые сведения, а в моментном ряду интервал - это промежуток времени между датами, на которые приведены сведения. В связи с этим значения показателей интервального ряда можно складывать. Значения показателей же моментного ряда складывать нельзя.

Основным требованием, предъявляемым к построению любых динамических рядов, является сопоставимость их уровней. Это требование должно обеспечиваться выбором одинакового интервала, единством методологии учета и расчета показателей.

Простейшими характеристиками динамического ряда являются: уровни ряда; абсолютный прирост; средний уровень ряда; темп роста; темп прироста.

Динамика зарегистрированных преступлений характеризуется следующими данными: 1996г. - 15 600, 1997г. - 17 300, 1998г. -18 100, 1999г. - 19 500, 2000г. - 20 000. Абсолютный прирост пре­ступлений в 1997г. по сравнению с 1996г. составляет 1700 (17 300 - 15 600), в 1998г. по сравнению с 1997г. - 800 (18 100 - 17 300) и т.д.

Средний уровень ряда, будучи обобщающим показателем для интервальных рядов и рядов средних величин, рассчитывается как среднее арифметическое из отдельных уровней.

Этот показатель характеризует среднегодовое значение уровней ряда за какой-то рассматриваемый период.

Для моментных рядов средний уровень рассчитывается несколько иначе.

Темпом роста называется отношение данного уровня к сравниваемому. Это относительный показатель, выраженный в процентах; если этот показатель исчисляется в долях, то он называется коэффициентом роста.

Темп роста показывает, во сколько раз уровень данного периода больше или меньше предыдущего или базисного. Темпы роста, как уже отмечалось, могут вычисляться цепным способом, когда каждый последующий уровень делится на каждый предыдущий, и базисным способом, когда каждый уровень делится на один и тот же уровень, взятый за базу.

Темп прироста - это относительный показатель, характеризующий, на сколько процентов один уровень больше или (меньше) другого уровня. Он может быть получен путем вычитания 100% из темпа роста. В нашем примере темп прироста будет равен 7% (107%-100%). Темп прироста можно получить также путем деле­ния абсолютного прироста на базисный уровень, по сравнению с которым рассчитан абсолютный прирост. В данном случае находим абсолютный прирост 1906988 - 1769565 = 137443 и делим его на базисный уровень, т.е.

Построение динамического ряда в отдельных случаях, когда показатели уровней последовательно увеличиваются или уменьшаются, может сразу обнаружить тенденцию развития явления во времени. Но такие случаи бывают редко. Чаще всего уровни ряда на протяжении определенного времени колеб­лются. Эти колебания вызываются одновременным действием случайных и систематических, краткосрочных и долговременных факторов. Задача состоит в том, чтобы, отбросив случайные факторы, выявить общую тенденцию в изменении уровней ряда.

Такая задача решается путем применения методов выравнивания динамических рядов.

Методы выравнивания динамических рядов можно разделить на две группы: эмпирические и аналитические.

Одним из самых простых эмпирических методов выравнивания динамических рядов является метод укрупнения интервалов. Суть его состоит в том, что в результате анализа ряда выбирается соответствующий укрупненный интервал и в пределах этого интервала складываются показатели уровней имеющегося ряда, в результате чего получается новый выровненный ряд. Рассмотрим пример.

Для выравнивания ряда выбираем интервал в три месяца и, сложив в пределах этих месяцев показатели уровней ряда, получим выровненный ряд:

Следует иметь в виду, что данный способ применим только к интервальным рядам. Для моментных рядов и рядов средних величин рассчитывается средний уровень по новым укрупненным интервалам.

Другим эмпирическим методом выравнивания динамических рядов является метод скользящей средней. Суть метода заключается в замене фактических уровней ряда скользящими средними, взятыми в пределах последовательно сдвигаемых интервалов. При этом способе по каждому укрупненному интервалу берется не сумма показателей, а их средняя арифметическая, причем после вычисления первой средней интервал переносится на один шаг вправо.

Для расчета скользящей средней можно, например, взять сумму пяти уровней и вычислить среднюю арифметическую этой суммы, разделив ее на пять. Далее, переходя на один интервал, подсчитывают среднюю для следующих пяти членов (начиная со второго) и так до конца.

В результате получается динамический ряд скользящих средних, который помогает более отчетливо выявить тенденции в развитии явлений.

Интервал в пять членов ряда выбран в данном случае произвольно. Можно производить сглаживание скользящими средними за 2, 3, 4 периода и т.д. в зависимости от характера динамического ряда.

Чем больше интервал, за который исчисляется средняя, тем более сглаженный ряд приближается к фактическому.

Помимо эмпирических методов существуют более сложные аналитические методы обработки динамических рядов. Сущность этих методов заключается в том, что на основе фактических данных подбираются подходящие для отражения тенденций развития явле­ния математические уравнения, по которым рассчитываются теоретические значения уровней ряда. Используя математические критерии сравнения, среди уравнений выбирается такое, которое наи­лучшим образом описывает экспериментальные данные. Затем с его помощью находят расчетные уровни ряда динамики, близкие к фактическим и выявляющие тенденции развития явления, нашедшего отражение в форме исходного динамического ряда. В качестве зависимостей для аналитической обработки динамических рядов могут выбираться прямолинейная, параболическая, гиперболическая, экспоненциальная, логарифмическая и др.

Простейшей математической формулой, выражающей тенденции развития, является формула прямой линии. Прямая линия характеризует равномерное изменение динамики. Выравнивание по прямой осуществляется методом наименьших квадратов. Этот метод обеспечивает минимальную разность между фактическими и теоретическими уровнями.

Выравнивание, как особый способ обработки динамических рядов, решает задачу выявления тенденций развития того или иного явления к настоящему моменту. Но при исследовании может возникнуть и другая задача, а именно: как данное явление будет развиваться в будущем.

Нахождение по известным значениям недостающих уровней внутри динамического ряда называется интерполяцией. Таким образом, экстраполяция и интерполяция - это распространение выводов, полученных из наблюдения над одной частью явления на другую его часть.

Метод экстраполяции заключается в нахождении значений, лежащих за пределами данного статистического ряда: по известным значениям статистического ряда находятся другие значения, лежащие за пределами этого ряда.

При экстраполяции выводы, которые сделаны при изучении тенденций развития явления в прошлом и настоящем, переносятся на будущее, т.е. в основе метода лежит предположение об определенной стабильности факторных признаков, влияющих на развитие данного явления.

Ввиду такого предположения экстраполяцию можно применять при прогнозировании на короткий срок, причем прогнозируемый период должен быть значительно меньше периода, за который выявлена тенденция изучаемого явления.

При экстраполяции используется следующая терминология и понятия : t1 — глубина ретроспекции; t2 — момент прогнозирования; tз — прогнозный горизонт; t2 – t1-интервал наблюдения (промежуток времени, на базе ко­торого исследуется история развития объекта прогнозирования); t3 – t2 — интервал упреждения (промежуток времени, на который разрабатывается прогноз).

Чем более устойчивый характер носят прогнозируемые процессы и тенденции, тем дальше может быть отодвинут горизонт прогнозирования. Как показывает практика, интервал наблюдения должен быть в три и более раза длиннее интервала упреждения. Как правило, этот период довольно короткий: до 1-го года. Метод экстраполяции не работает и при скачкообразных процессах.

Метод экстраполяции легко реализуется на персональных компьютерах. В частности, он особенно оперативен в реализации при использовании табличного процессора MS Excel, который можно установить практически на все современные персональные компьютеры.

Однако следует заметить, что при этом необходимо быть внимательным при выборе вида нелинейной функции линии тренда. Чем больше значение коэффициента достоверности R2, тем точнее сглаживающая кривая описывает эмпирические данные, но долгосрочная тенденция отражается тогда в меньшей степени. Поэтому при интерпретации полученной линии тренда, когда она неограниченно растет или резко уменьшается, надо учитывать также и физический смысл.

Следует иметь в виду и то обстоятельство, что экстраполяция - это не конечный результат, а отправной момент прогнозирования. Прогноз разрабатывается с учетом результатов экстраполяции, но с привлечением дополнительной информации, не содержащейся в самом динамическом ряду.

Если значения уровней динамического ряда последовательно увеличиваются или последовательно уменьшаются, то экстраполяцию можно осуществлять методом среднего геометрического. В этом случае находится средний темп роста, а он, как нам уже известно, определяется с помощью среднего геометрического. Умножая последний известный уровень ряда на средний темп, находим первый расчетный уровень; умножая его на средний темп роста, находим второй расчетный уровень и т.д.

Для динамических рядов, значения показателей уровней которых колеблются, можно применять аналитические методы вырав­нивания.

Аналитическая обработка интервальных рядов динамики в целях выделения из их уровней случайных компонентов и установления тенденций развития осуществляется с помощью ряда способов, одним из наиболее часто применяемых и теоретически обоснованных среди которых является метод наименьших квадратов.

Посредством выравнивания по способу наименьших квадратов не только устанавливается общая тенденция развития явления, но и дается количественная характеристика изменения уровней ряда.

Выравнивание может быть произведено по прямой или какой-либо другой линии, выражающей функциональную зависимость уровня динамического ряда от времени:

Выравниванию предшествует теоретический анализ динамического ряда в целях познания сущности исследуемого явления и законов его развития, на основе чего устанавливаются характер динамики и тип необходимой кривой. Теоретический, качественный анализ является основой и в дальнейшем преобразовании ряда. Выравнивание же выступает лишь в качестве технического приема, инструмента, который способствует теоретическому анализу. Если явление развивается с относительно стабильными абсолютными приростами ∆У, то на практике чаще всего применяется выравнивание по прямой линии.

При выравнивании ряда динамики по прямой линии фактические уровни У ряда заменяют теоретическими Уt, которые равномерно возрастают или убывают, так как прямой линией характеризуется равномерное изменение динамики.

Метод наименьших квадратов предполагает в этом случае, что расчетные уровни ряда должны лежать на прямой линии, которая ближе всего подходит к линии фактических уровней ряда и наиболее точно отражает тенденции изменения ряда. Найденная прямая обладает следующим свойством: сумма квадратов отклонений ее ординат от соответствующих ординат исходного ряда, т.е. разность между экспериментальными и теоретическими уровнями при одних и тех же абсциссах является наименьшей:

В приведенной формуле значения t всегда известны, а для нахождения нужно определить параметры прямой а и b.

Для нахождения параметров линейного уравнения получается система линейных уравнений:

В целях облегчения нахождения параметров а и b систему уп­рощают, придавая условно показателям времени t такие значения, при которых их сумма становится равной нулю. Для этого в рядах с нечетным числом членов серединный член обозначается нулевым интервалом t = 0, а другие члены получают условные номера -1, -2, -3 и т.д. и +1, +2, +3 и т.д. Если число членов ряда четное, то два серединных члена обозначаются нулевыми интервалами, а другие члены, как и ранее, -1, -3, -5, -7 и т.д., +1, +3, +5,+7 и т.д.

При таком подходе рассмотренная выше система уравнений упрощается и принимает следующий вид:

Определив параметры а и b, легко вычислить теоретические (расчетные) уровни, т.е. ординаты точек искомой прямой Уt.

Аналитическая обработка динамического ряда позволяет за колебаниями уровней исходного ряда обнаружить определенную тенденцию (тренд), количественным выражением которой будет значение параметра b, и экстраполировать динамический ряд в будущее. При этом следует иметь в виду, что интервал прогноза должен быть гораздо короче того периода, за который выявлена тенденция прогнозируемого процесса.

Метод корреляционно-регрессионного анализа и метод сценариев при обосновании логистических решений.

Существующие между явлениями формы и виды связей весьма разнообразны по своей классификации. Предметом статистики являются только такие из них, которые имеют количественный характер и изучаются с помощью количественных методов. Рассмотрим метод корреляционно-регрессионного анализа, который является основным в изучении взаимосвязей явлений.

Данный метод содержит две свои составляющие части — корреляционный анализ и регрессионный анализ. Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами.

Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая — от 0,1 до 0,3; умеренная — от 0,3 до 0,5; заметная — от 0,5 до 0,7; высокая — от 0,7 до 0,9; весьма высокая (сильная) — от 0,9 до 1,0. Она используется далее в примерах по теме.