Теория массового обслуживания

Теория массового обслуживания используется для исследования систем управления, в которых имеется необходимость пребывать в состоянии ожидания. Это является следствием вероятностного характера возникновения потребности в обслуживании и разброса показателей соответствующих обслуживающих систем. В таких случаях исследуемую систему представляют в виде системы массового обслуживания.

Задача заключается в построении математической модели, связывающей заданные условия работы СМО с эффективностью ее работы.

Аналитические математические модели СМО в настоящее время могут быть построены только для определенных условий (см. [6.53; 6.44]).

Главным является требование к потоку заявок, который должен быть простейшим. Входной поток заявок — это последовательность событий, следующих одно за другим в какие-то случайные моменты времени. Поток событий называется простейшим, если он стационарен (вероятные характеристики не зависят от времени), ординарен (события появляются поодиночке, а не группами), не имеет последствий (для двух участков времени число событий, попадающих на один участок, не зависит от того, сколько попало на другой).

Если интервалы времени t между событиями подчиняются показательному распределению 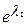(где l_t — интенсивность потока заявок), то поток называется пуассоновским. При пуассоновском входном потоке заявок процесс, протекающий в СМО, называется марковским, и в нем можно установить аналитические зависимости между условиями операции, элементами решения и показателями эффективности.

Математические модели для различных СМО классифицируют по следующим признакам:

¨ с отказами заявок или очередью;

¨ ограничением очереди заявок или без него;

¨ приоритетом обслуживания некоторых заявок или без приоритета;

¨ много- или однофазным обслуживанием (в первом случае обслуживание складывается из нескольких этапов);

¨ открытой или замкнутой СМО (в открытых СМО характеристики потока не зависят от состояния СМО).

Обычно для марковских случайных процессов в СМО строят граф ее состояний и возможных переходов, а затем для этого графа составляют и решают уравнения Колмогорова.