Синтез систем управления методами

Математического программирования

¨ сущность и содержание математического программирования

¨ общая характеристика методов математического программирования

¨ методы решения задач линейного программирования

¨ методы решения задач нелинейного программирования

¨ методы решения задач дискретного (целочисленного) программирования

¨ методы динамического программирования

¨ методы стохастического программирования

Сущность и содержание математического

Программирования

Методы математического программирования относятся к численным методам поиска оптимальных решений, которые позволяют найти решение только для конкретных значений параметров. Содержание математического программирования составляют теория и методы решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). В упрощенной постановке задача оптимизации может быть сформулирована следующим образом.

Имеется набор параметров х₁, ..., х_п и функция F(x). Требуется определить такую совокупность параметров из множества X, для которой функция F(x) принимает наибольшее или наименьшее значение. Функция F(x) получила название целевой функции.

Методы решения задач такого типа в литературе именуются методами математического программирования.

Термин "программирование" не связан с составлением программ для ЭВМ, но обусловлен тем, что при решении такого рода задач математическими средствами составляется программа действий.

Независимо от конкретной предметной ориентации задачи, решаемые методами математического программирования, с формальной точки зрения сводятся к одной постановке.

При выполнении условий

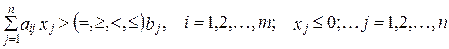
необходимо найти совокупность параметров (план)

,

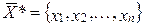при котором функция (целевая функция)

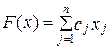
принимает наибольшее или наименьшее значение.

Условия 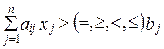называются ограничениями задачи. Дополнительно к условиям может быть задано требование целостности всех или нескольких переменных х_j.

Вектор X̅* называется оптимальным планом задачи или оптимальным решением, так как его нахождение связано с отыскиванием конкретных значений параметров управления.

При решении задач математического программирования широко используются свойства линейных уравнений и неравенств, различные понятия, связанные с максимумами и минимумами функций, гладкими функциями, выпуклыми множествами и др.